|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Singer I. — Bases in Banach spaces II |
|
|
 |
| Предметный указатель |
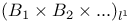 241 241
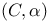 358 358
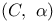 -basis 358 -basis 358
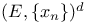 263 263
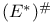 550 550
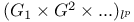 425 425
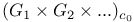 425 425
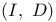 -conditional basis 811 -conditional basis 811
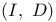 -conditional decomposition ( -conditional decomposition (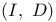 -conditional basis of subspaces) 826 -conditional basis of subspaces) 826
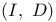 -conditional Schauder decomposition 826 -conditional Schauder decomposition 826
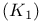 204 204
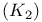 330 330
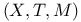 601 601
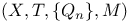 551 551
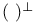 61 61
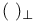 48 48
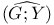 48 48
![$2^{[1, n]}$](/math_tex/29639624782d62eac109c1af157ffd5982.gif) 10 10
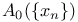 38 38
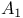 152 553 152 553
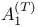 351 351
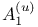 153 153
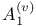 341 341
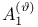 583 583
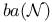 196 196
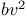 366 366
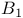 768 768
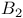 768 768
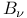 820 820
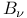 -space 820 -space 820
 -decomposition 531 -decomposition 531
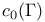 6 579 6 579
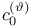 591 591
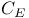 349 349
![$C_{E}([1, \omega])$](/math_tex/164b899b74c392252f0b3db3dfb606cf82.gif) 581 581
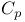 425 425
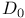 504 504
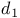 487 487
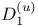 541 541
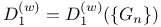 519 519
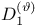 623 623
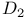 500 500
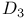 513 513
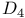 512 512
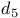 513 513
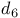 513 513
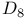 525 525
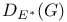 662 662
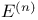 508 508
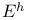 660 660
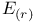 35 35
 415 542 811 415 542 811
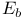 294 294
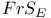 38 38
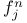 29 29
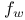 15 15
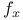 659 659
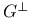 61 61
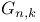 13 13
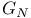 26 26
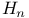 26 26
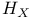 659 659
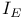 1 1
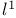 -system 864 -system 864
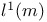 -system 864 -system 864
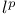 -decomposition 531 -decomposition 531
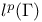 6 579 6 579
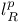 36 36
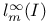 861 861
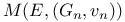 500 500
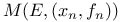 190 190
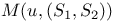 802 802
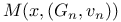 500 500
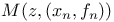 191 191
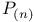 49 49
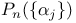 190 190
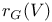 90 90
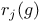 9 9
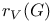 90 90
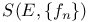 189 189
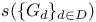 824 824
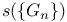 514 514
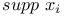 6 6
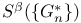 514 514
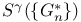 514 514
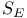 38 38
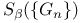 514 514
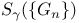 515 515
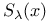 586 586
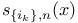 575 575
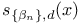 579 579
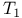 823 823
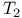 824 824
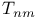 370 370
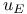 511 511
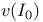 576 576
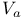 200 200
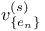 803 803
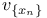 49 284 49 284
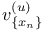 309 309
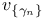 199 199
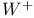 9 9
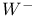 9 9
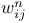 763 763
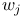 26 26
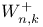 13 13
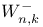 13 13
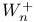 26 26
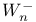 26 26
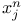 28 28
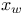 13 13
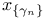 198 198
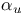 109 109
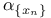 103 103
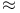 210 507 210 507
 -dual 514 -dual 514
 -perfect 515 -perfect 515
 -predual (sub- -predual (sub- dual) 515 802 dual) 515 802
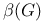 768 768
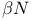 592 592
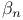 768 768
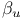 109 109
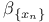 106 106
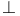 729 729
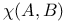 793 793
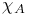 208 208
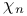 515 515
 36 36
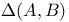 793 793
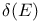 795 795
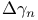 365 365
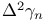 365 365
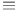 55 55
 -equivalent 50 168 -equivalent 50 168
 -basis 404 -basis 404
 -dual 514 -dual 514
 -perfect 515 -perfect 515
 -predual (sub- -predual (sub- dual) 515 802 dual) 515 802
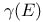 308 308
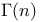 768 768
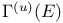 866 866
 49 49
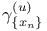 866 866
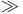 132 507 132 507
 141 141
 -approximation property ( -approximation property ( -metric) 291 768 -metric) 291 768
 -approximative basis 275 -approximative basis 275
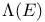 770 770
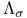 381 381
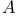 514 514
| 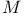 141 141
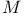 -space 824 -space 824
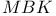 -space 824 -space 824
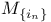 148 148
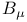 816 816
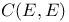 518 518
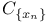 564 564
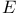 23 23
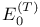 361 361
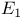 91 91
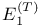 361 361
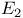 91 91
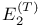 361 361
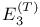 361 361
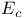 799 799
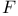 422 422
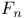 423 423
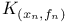 564 564
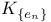 560 560
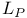 -space 536 821 -space 536 821
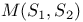 518 518
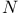 55 55
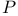 587 587
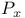 566 566
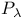 497 497
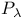 -space 497 800 -space 497 800
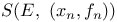 259 259
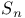 64 64
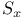 574 574
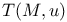 5 5
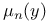 140 380 140 380
 581 581
 -linearly independent sequence 104 -linearly independent sequence 104
 -linearly independent sequence of subspaces 501 801 -linearly independent sequence of subspaces 501 801
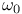 822 822
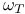 -linearly independent sequence 786 -linearly independent sequence 786
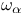 648 648
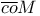 40 40
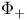 -operator 109 -operator 109
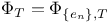 786 786
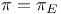 38 511 38 511
 -basis 409 -basis 409
 -basis (Schauder operator basis, -basis (Schauder operator basis,  system) 407 791 system) 407 791
 -basis, strict 407 -basis, strict 407
 -basis, weak 409 -basis, weak 409
 -basis, weak* 409 -basis, weak* 409
 -ring 801 -ring 801
 -space 791 -space 791
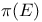 792 792
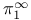 -basis ( -basis (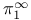 decomposition) 417 792 decomposition) 417 792
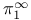 -space 792 -space 792
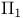 92 92
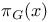 334 334
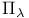 -basis 407 -basis 407
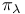 -basis ( -basis (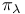 decomposition, decomposition, 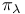 system) 407 791 system) 407 791
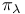 -basis, strict 407 -basis, strict 407
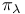 -basis, weak 409 -basis, weak 409
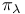 -basis, weak* 409 -basis, weak* 409
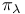 -space 791 -space 791
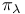 -space, dual 793 -space, dual 793
 475 663 475 663
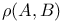 793 793
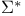 98 98
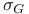 49 49
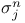 28 28
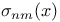 350 350
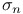 370 370
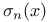 350 350
 47 67 203 498 47 67 203 498
 115 115
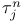 28 28
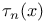 386 404 386 404
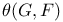 533 533
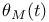 560 560
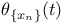 564 564
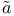 64 64
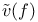 659 659
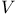 54 54
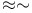 209 507 209 507
 -close 411 -close 411
 -isometry 120 -isometry 120
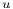 109 109
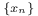 106 106
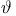 -linearly independent transfinite sequence 814 -linearly independent transfinite sequence 814
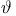 -linearly independent transfinite sequence of subspaces 830 -linearly independent transfinite sequence of subspaces 830
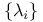 -linearly independent sequence 155 -linearly independent sequence 155
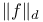 822 822
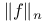 81 524 81 524
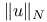 258 258
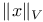 92 92
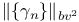 366 366
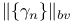 365 365
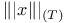 361 361
(![$[h_{n}]$](/math_tex/6f12be778bac15eff2bb489957c9adb882.gif) , ,  )-near 115 )-near 115
(![$[h_{n}]$](/math_tex/6f12be778bac15eff2bb489957c9adb882.gif) , ,  )-near, weakly 115 )-near, weakly 115
( , ,  )-approximation property 304 )-approximation property 304
(F) 704
(F)-norm 704
(F)-space 704
(p, r) 381
a(E) 518
A(E, E) 518
A.f.c.f. = associated family of coefficient functionals 574
A.f.f. = associated family of functionals 691
A.s.c.f. = associated sequence of coefficient functionals 47
A.s.c.p. = associated sequence of coordinate projections 486
A.s.f. = associated sequence of functionals 166
A.t.s.c.f. = associated transfinite sequence of coefficient functionals 582
A.t.s.c.p. = associated transfinite sequence of coordinate projections 622
Acute angled sequence 564
Acute angled set 560
AD-space 190
Admissible mapping 189
Admissible sequence for a generalized basis 189
Admissible sequence for a quasi-basis 278
Admissible sequence for a quasi-decomposition 539
Admissible space 717
AK-space 190
Alexander, F.E. 864
Altshuler, Z. 751 864
Amir, D. 828 829 832 833
Angular modulus of a sequence 564
Angular modulus of a set 560
Approximation problem 717
Approximation property 5
Approximation property,  -duality 314 -duality 314
Approximation property,  -projection 413 -projection 413
Approximation property,  -uniform 818 -uniform 818
Approximation property,  -uniform projection 818 -uniform projection 818
Approximation property, bounded 291
Approximation property, bounded compact 724
Approximation property, bounded projection 413
Approximation property, compact 724
Approximation property, metric 291
Approximation property, projection 413
Approximation property, separable range 817
Approximation property, uniform 818
Approximation property, uniform projection 818
Approximative basis 275
Approximative basis of elements 275
Approximative basis of operators 275
Approximative basis,  -projection 413 -projection 413
Approximative basis, projection 413
Approximative basis, weak 323
Approximative basis, weak* 323
Aronszajn, N. 766
Arsove, M.G. 758 759 810 811 832
Ascending function 649
Ascending function, strictly 587 649
Asplund, E. 834
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



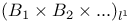
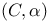
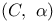 -basis
-basis 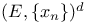
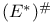
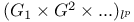
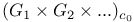
 -conditional basis
-conditional basis 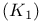
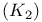
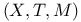
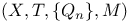
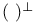
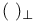
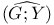
![$2^{[1, n]}$](/math_tex/29639624782d62eac109c1af157ffd5982.gif)
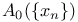
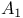
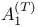
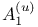
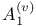
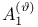
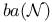
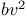
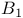
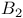
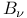
 -decomposition
-decomposition 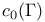
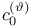
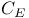
![$C_{E}([1, \omega])$](/math_tex/164b899b74c392252f0b3db3dfb606cf82.gif)
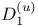
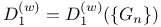
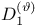
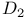
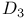
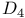
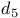
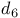
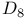
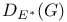
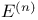
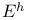
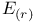

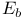
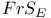
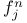
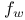
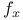
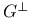
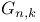
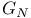
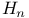
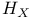
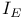
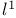 -system
-system 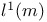 -system
-system 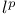 -decomposition
-decomposition 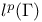
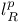
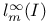
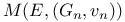
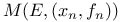
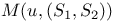
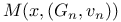
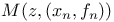
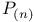
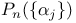
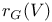
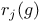
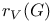
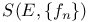
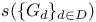
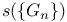
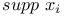
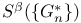
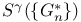
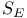
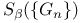
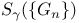
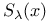
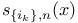
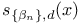
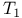
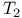
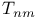
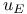
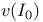
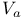
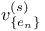
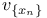
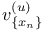
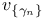
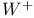
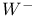
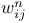
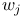
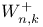
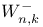
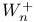
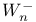
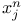
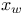
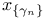
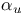
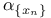
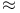
 -dual
-dual 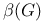
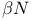
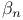
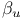
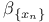
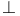
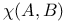
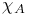
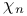

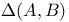
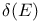
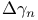
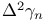
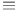
 -equivalent
-equivalent  -basis
-basis 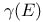
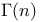
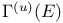

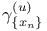

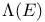
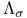
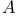
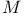
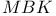 -space
-space 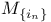
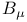
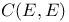
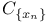
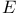
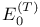
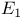
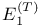
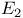
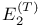
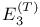
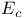
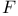
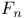
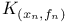
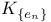
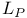 -space
-space 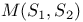
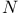
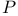
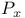
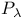
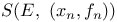
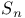
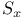
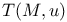
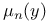

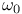
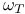 -linearly independent sequence
-linearly independent sequence 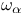
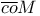
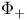 -operator
-operator 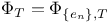
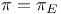
 -basis
-basis  -basis (Schauder operator basis,
-basis (Schauder operator basis, 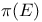
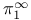 -basis (
-basis (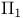
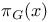
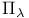 -basis
-basis 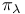 -basis (
-basis (
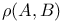
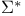
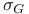
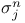
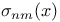
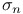
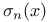

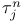
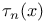
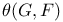
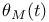
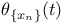
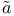
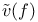
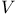
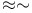
 -close
-close 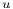
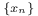
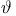 -linearly independent transfinite sequence
-linearly independent transfinite sequence 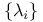 -linearly independent sequence
-linearly independent sequence 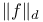
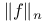
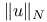
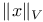
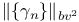
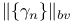
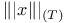
![$[h_{n}]$](/math_tex/6f12be778bac15eff2bb489957c9adb882.gif) ,
,  )-near
)-near  ,
,