Авторизация
Поиск по указателям
Browder A. — Mathematical Analysis: An Introduction
Обсудите книгу на научном форуме Нашли опечатку?
Название: Mathematical Analysis: An IntroductionАвтор: Browder A. Аннотация: Among the traditional purposes of such an introductory course is the training of a student in the conventions of pure mathematics: acquiring a feeling for what is considered a proof, and supplying literate written arguments to support mathematical propositions. To this extent, more than one proof is included for a theorem - where this is considered beneficial - so as to stimulate the students' reasoning for alternate approaches and ideas. The second half of this book, and consequently the second semester, covers differentiation and integration, as well as the connection between these concepts, as displayed in the general theorem of Stokes. Also included are some beautiful applications of this theory, such as Brouwer's fixed point theorem, and the Dirichlet principle for harmonic functions. Throughout, reference is made to earlier sections, so as to reinforce the main ideas by repetition. Unique in its applications to some topics not usually covered at this level.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1996Количество страниц: 370Добавлена в каталог: 11.12.2011Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Infimum 15 Injective 3 178 Inner product 128 178 271 282 Integers 4 Integrable 230 Integral of differential form 294 Integral of form over manifold 301 Integral of nonnegative function 228 Integral of simple function 227 Integral, change of variables 112 Integral, existence 101—105 Integral, improper 114 Integral, improper is a measure 227 228 Integral, linear change of variables 241 Integral, linearity of 227 229 Integral, Riemann 98—114 201 231—233 Integral, smooth change of variables 241—244 Integration by parts 112 247 Interchange of limit and 113 Interchange of series 113 Interchange, linearity of 230 Interior 125 Interior point 124 Intermediate Value Theorem 59 Intersection 1 interval 18—19 Interval in 204 Interval, closed 19 Interval, open 19 Intervals, nested sequences 19 Inverse function 60 191 Inverse function theorem 192 257 Isolated point 125 Isomorphism 282 Isomorphism, natural 270 Jacobi, C.G.J 252 Jacobian 182 294 Jacobian matrix 196 Jensen, J.W.L 252 Jordan, C 121 Jordan, C, kernel 178 Kolmogorov, A 221 kronecker 6 269 276 Kronecker epsilon 276 311 230 Kronecker, L 54 Kronecker, multi-index 271 Lagrange multipliers 266 Lagrange, J. — L 95 96 Laplacian (Laplace operator) 314 Largest integer in 15 Lebesgue, H 173 221 252 Leibniz, G 53 82 95 121 Lemma 291 Lemniscate 258 Level surface 194 Levi — Civita, T 284 Levi, B 228 Liminf 34 Liminf of sets 219 Limit point 125 Limsup 34 Limsup of sets 219 Lindemann, F 27 Line segment 185 Linear algebra 176 181 Linear functional 269 Linear transformation 176 240 Linear transformation, metrics on 179 Liouville's theorem on algebraic numbers 20 Liouville's theorem on harmonic functions 317 Liouville, J 20 27 219 Lipschitz condition 138 Local coordinate 255 Locally connected 152 Lower semicontinuous 70 159 Lower sum 100 L’Hospital, G. — F.-A 96 L’Hospital’s Rule 86 Manifold 253 254 Manifold, construction of 258—259 Manifold, examples of 256—258 Manifold, orient able 263 Manifold, orientation of 263 Manifold, oriented 263 MAP 3 Map, closed 134 Map, linear 176 Map, open 134 Mapping (see Map) Matrix 176—178 Matrix product 177 Maximal 13 Maximal rank 259 Maximum principle 316 Maximum, existence of 59 142 Maximum, local 83 184 266 Maxwell, J.C 321 Mean value inequality 186 Mean value theorem 83 185 Mean Value Theorem for harmonic functions 315 Mean Value Theorem for Integrals 108 Measurability criteria 224 Measurable function 223 Measurable, Lebesgue 213 215—218 Measure 206 Measure, Borel 206 Measure, counting 203 Measure, determined by 238 239 Measure, Hausdorff 215 321 Measure, inner 220 222 Measure, Lebesgue 213 215 Mertens, F 53 Metric 127 Metric space 128—131 214 236 Metric, product 132 Metric, standard on 129 Metric, standard on R 128 Metric, uniform on C(X, Y) 145 Miintz — Szasz theorem 174 Minimal 13 Minimum, existence of 142 Minimum, local 83 184 266 Minkowski, H 252 Moebius strip 258 267 319 Moebius, A.F 283 Monge, G 267 Monotone, convergence theorem 228 248 Monotone, function 56 Monotone, sequence 33 64 Monotone, set function 203 209 Multinomial coefficient 190 Nabla ( 289 Natural 176 Neighborhood 56 124 Nested compact sets 141 Net 153 Newton, I 53 95 121 Nonsingular 178 Norm 129 Normal derivative 314 Normal vector 260 Normal vector field 312 Null space 178 Numbers, algebraic 20 Numbers, complex 25 Numbers, extended real 15 203 Numbers, natural 2 4 Numbers, operations 223 Numbers, rational 5 Numbers, rational countability of 7 Numbers, real 15 Numbers, real existence of 21 23 Numbers, real uncountability of 19 Numbers, satanic 221 Numbers, transcendental 20 Open cover 140 Open set 123 215 Operator norm 179 Oriented, positively 263 Orthogonal transformation 240 Osgood, W.F 137 153 Ostrogradski, M.V 321 Outer measure 209 Outer measure, Hausdorff 210 221 Outer measure, Lebesgue 210 Outer measure, Lebesgue — Stieltjes 210 221 Outer measure, metric 214 221 Parse val’s relation 169 Partial derivative, Leibniz notation 197 Partial derivative, multi-index notation 190 Partial derivatives 186 191 Partial derivatives, higher order 189 Partial derivatives, mixed 189 Partial order 3 Partition 2 98 Partition of unity 298 299 Path 159 Path, length of 159 permutations 273 Perron FVobenius theorem 319 Picard’s Theorem 138 Piecewise smooth 168 Plato 26 Poincar 6 Point mass 203 Power series 90 Power series of matrices 181 Power set 2 Precompact 144 primitive 110 Projection map 133 Pseudometric 166 220 236 Radius of convergence 90 Radon, J 221 RANGE 3 178 refinement 98 Relation 2 Relation, equivalence 2 217 Ricci, G 284 Riemann integral (see Integral) Riemann sum 99 Riemann — Lebesgue lemma 168 Riemann, B 53 121 267 Riemannian structure 293 Riesz — Fischer theorem 237 Riesz, F 252 Rogers, L.J 252 Rolle, M 96 Root, existence of 18 Row vector 183 269 Russell, B 27 Schwarz, H.A 109 Second axiom of countability 131 Seidel, P 73 Selection 98 Separable 126 220 SEQUENCE 4 28 Sequence in topological space 135 Sequence of functions 62 Sequence of measures 208 Sequence, Cauchy 36 136 Sequence, convergent 28 Sequence, divergent 28 Sequence, monotone 33 Sequence, uniformly Cauchy 63 Series 39 Series, absolutely convergent 40 Series, alternating 43 Series, Cauchy product of 49 Series, comparison test 40 Series, conditionally convergent 40 Series, engineers test 39 Series, for e 42 Series, Fourier 122 164 Series, geometric 41 Series, harmonic 30 41 42 Series, partial sum 39 Series, ratio test 42 Series, rearrangement of 45 Series, root test 41 Series, telescoping 41 Series, trigonometric 174 Series, unordered 47 Set 1 Set, Borel 205 214 215 220 224 Set, closed 124 Set, convex 96 152 Set, directed 53 Set, finite 6 Set, infinite 6 Set, Lebesgue measurable 248 Set, unmeasurable 217 Sierpinski, W 154 174 Sign of permutation 273 Simple function 225 Simple function, canonical representation 225 Smooth 254 255 Smooth, forms 286 Space, door 150 Space, Euclidean 123 Space, Hausdorff 135 Space, Hilbert 130 Space, metric 128 Space, topological 123 Square root algorithm 31 Stokes, G 73 321 Stokes’ Theorem 303 Stokes’ theorem, classical case 319 Stone Weierstraas theorem 158 Stone, M 158 174 Stone’s theorem 157 Subgroup 218 Subsequence 34 subspace 131 Summable 230 Summation by parts 44 Summation convention 281 Support line 81 Supremum 15 surface 253 257 Surjective 3 178 Symmetric tensor 282 Tangent bundle 260 Tangent space 253 260 Tangent vector 260 Tangent vector, characterization of 261 262 Taylor polynomial 89 191 Taylor, B 96 Taylor’s Theorem 89 96 120 Taylor’s theorem in n variables 190 Tensor field 285 Tensor field of class 286 Tensor product 271 Tensor, alternating 272 Tensor, covariant 270 Tensor, elementary 283 Tensor, rank of 270 Tensors of rank r basis for 271 Thomson, W. (Kelvin) 321 Toeplitz, O 26
Реклама
 |
|
О проекте
|
|
О проекте



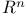
 -system
-system 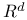
 )
)