|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| DeWitt B.S. — The global approach to quantum field theory (Vol. 1) |
|
|
 |
| Предметный указатель |
Functional 5
Functional derivative 5
Functional derivative left functional derivative 5
Functional derivative right functional derivative 5
Functional derivative, comma notation for 8
Functional derivative, covariant functional derivative 255ff
Functional integral for Bose oscillator 857—858
Functional integral for expectation values 662—663
Functional integral for Fermi doublet 830—831
Functional integral for Fermi oscillator 844
Functional integral for gauge fields 463 465 468 493—494 515—516 662—663
Functional integral for nonlinear fields 409
Functional integral for nonrelativistic particle in flat space 803
Functional integral for relativistic particle in Minkowski spacetime 935
Functional integral for simple Fermi system 813 817—818
Functional integral, Feynman’s integral 171ff
Fundamental domains (in path-integral homotopy) 227
Gamma function 1018
Gauge algebra 19
Gauge field 4
Gauge fixing 496
Gauge group 19
Gauge group, full gauge group 19
Gauge group, proper gauge group 19
Gauge group, rigidity of 488
Gauge invariant effective action 500
Gauge theories 456ff
Gauge theories without ghosts 513ff 676ff
Gauge theories, “in—in” formalism for 676ff
Gauge transformations 4 20
Gauge transformations for quantum electrodynamics 732
Gauge transformations little gauge transformations 20 770
Gauge transformations of gravitational field 101 784
Gauge transformations of Yang — Mills field 755
Gauge transformations, big gauge transformations 20 770
Gauge transformations, boundary conditions for 771
Gaussian integration over  994—996 994—996
Geodesic normal coordinates 275ff
Geodesic normal fields 513—514
Geodesic normal fields for “in-in” formalism 679
Geodetic parallel displacement matrix or operator 283—284 534ff
Ghost fields 22 472
Ghost fields, integrating out 493—494
Ghost fields, toy model for 868ff
Ghost number 22
Ghost operator 34 458
Ghost operator for gravitational field 785
Ghost operator for quantum electrodynamics 732
Ghost operator for Yang — Mills field 757
Ghost operator, mode functions for 399
Ghost operator, nonsymmetric ghost operator 101 Off
Ghost operator, propagator for 458 465
Ghost operator, Wronskian relations for 399
Ghosts for ghosts 959ff
Global conformal group 110ff
Graphs and subgraphs 700ff
Grassmann algebra 976
Gravitational field 783ff
Gravitational field, action functional for 783
Gravitational field, coupled with Yang — Mills field 793
Gravitational field, energy, momentum and angular momentum in 790—791
Gravitational field, gauge invariant ultralocal metric for 785—786
Gravitational field, gauge transformations of 101 784
Gravitational field, ghost operator for 785
Gravitational field, Jacobi field operator for 785
Gravitational field, one-loop effective action for 788
Gravitational field, one-loop finiteness of 788
Gravitational field, stress-energy density of 789
Green’s functions see also Feynman propagator
Green’s functions of n-dimensional Laplacian operator 1021
Green’s functions, coherent 42ff
Green’s functions, equality of left and right 37
Green’s functions, for “in-in” formalism 668
Green’s functions, Landau 44
Green’s functions, off shell 42
Green’s functions, reciprocity relations for 38
Green’s functions, relations between 40
Green’s functions, retarded and advanced 36
Green’s functions, transformation laws for 45
Hamilton — Jacobi equations 215
Hamiltonian 52
Hamiltonian, Hamiltonian operator 231 259ff 262
Hamilton’s principle (of stationary action) 13ff 17 29
Harfle — Hawking vacuum 640
Harfle — Hawking vacuum, instability of 658
Harfle — Hawking vacuum, reactions of a monopole detectors to 646
Harfle — Hawking vacuum, temperature of 643
Harfle — Hawking vacuum, viewed as a gas 643ff
Hawking radiation 656
Heat kernel 275ff
Heat kernel for the spinor field 55Iff
Heat kernel, asymptotic expansion of 285 541
Heat kernel, recursion relations for 286 541
Heat kernel, Schwinger’s representation of 532
Helicity 905 909 914 919
Helicity, space inversion law for spinor helicity 728
Hole theory 370ff
Homotopy (in path integrals) 220ff
Homotopy (in path integrals), covering translations 222
Homotopy (in path integrals), fundamental domains 227
Homotopy (in path integrals), fundamental group 221
Homotopy (in path integrals), relation to homology and cohomology 223ff
Homotopy (in path integrals), universal covering space 221—2
Homotopy in quantum field theory 232—233
Horizontal projection operator 457
Horizontal projection operator for “in-in” formalism 678
Imperfect measurements 159
instantons 781—783
Integral of  1023 1023
Integral of  , corollaries of 1023—1025 , corollaries of 1023—1025
Integration in  and and  979—81 979—81
Integration in  and and  , Gaussian integration 994—996 , Gaussian integration 994—996
Integration in  and and  , integration over , integration over  990ff 990ff
Internal sources 79
Interpolating field 72
Interpolating field, invariance under changes of 73
Interpolating field, invariance under changes of, in quantum field theory 446ff
Invariance of ghost-free loop graphs 520ff
Invariance transformations 14ff
Invariance transformations, commutator of 17
Invariant flows 14ff
Invariant flows, existence implies massless fields 92
Invariants (physical observables) 25
Invariants (physical observables) in presence of ghost fields 492—493
Invariants (physical observables), absolute 25
Invariants (physical observables), conditional 25
Isotropic curvature 1042
Jacobi field operator 31
Jacobi field operator for gravitational field 785
Jacobi field operator for quantum electrodynamics 732—733
Jacobi field operator for Yang — Mills field 757
Jacobi field operator for “in-in” formalism 665
Jacobi field operator, self adjointness of 32
Jacobi fields (small disturbances) 30ff 236
Jacobi fields (small disturbances) as generators of finite disturbances 61
Jacobi fields (small disturbances), Cauchy problem for 56ff
Jacobi fields (small disturbances), quantum Jacobi fields 439
Jacobi identity for Peierls bracket 50
Jacobi identity for supercommutators 1005
Killing fields 80
Killing vector fields 107ff
Klein paradox, bosonic 335
Klein paradox, fermionic 372
Kruskal coordinates 630—631
Lagrangian 13
Lagrangian for linear scalar field 291
Lagrangian for massive linear vector field 312
Lagrangian for nonrelativistic particle in curved space 252
Lagrangian for spinor field 351
Lagrangian for spinor field,  -function for 925 -function for 925
| Lagrangian for spinor field, 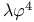 model 920ff model 920ff
Lagrangian for spinor field, one-loop effective action for 923
Lagrangian for spinor field, physical mass for 928
Lagrangian for spinor field, renormalization group for 923
Lagrangian for spinor field, spontaneous symmetry breaking in 928—929
Legendre transform (relation between W and  ) 413 ) 413
Lehmann — Symanzik — Zimmermann (LSZ) theorem 427ff
Linear fields possessing invariant flows 396ff
Linear fields possessing invariant flows, Bogoliubov relations for 403
Linear fields possessing invariant flows, mode functions for 398
Linear fields possessing invariant flows, Wronskian relations for 398—399
Linear operators on super Hilbert spaces 1001—1002
Local conformal group 109
Local conformal group, structure constants with diffeomorphism group 109
Local conformal transformations 109
Local Lorentz frames (field of) 341
Localization-decoherence 200ff
Loop expansion 241ff 416ff
Loop expansion for gauge theories without ghosts 518
Loop expansion of reduced effective action 496ff
Lorentz frame bundle 341
Lorentz frame group 342
Lorentz group O(1, n-1), generators of 342 538—539
Manifest covariance 26ff
Many worlds 140 207
Many worlds, unobservability of splitting into 14Iff
Mass operator 745
Massless scalar field in compact universe 31 Off
Massless vector field see Electromagnetic field
Measure functional 168
Measure functional for gauge fields 468 470 475
Measure functional for gauge fields loop decomposition of 478ff
Measure functional for Lagrangian path integral 217 257
Measure functional for phase-space path integral 219
Measure functional for “in-in” formalism 673
Measure functional, approximate expression for 170
Measure functional, role as volume density 173
Measure functional, role of in Wick rotation 481 692ff
Measurement situation 207
Measurement theory 117ff
Measurement theory, apparatus inertia 118
Measurement theory, compensation term 122
Measurement theory, disturbance in the apparatus 120
Measurement theory, electric field measurement 125ff
Measurement theory, error analysis 12Iff
Measurement theory, quantum theory of measurement 131 ff
Measurement theory, Stern — Gerlach experiment 123ff
Measurement theory, system and apparatus 117
Measurement theory, system-apparatus coupling 117
Minimal coupling to gravitational field 104
Minimal subtraction 704
Mode functions for Bose oscillator 850
Mode functions for electromagnetic field 397 904
Mode functions for Fermi oscillator 840
Mode functions for fourth order system 863
Mode functions for linear scalar field 297ff 309ff
Mode functions for massive antisymmetric tensor field 881—882
Mode functions for massive linear vector field 315 878
Mode functions for massive spin-1 field 899
Mode functions for massive symmetric tensor field 885—886
Mode functions for massless antisymmetric tensor field 971
Mode functions for massless spin-1 field 918
Mode functions for massless symmetric tensor field 907
Mode functions for scalar field in Schwanzschild black hole 628 633—635
Mode functions for spinor field 362ff 892 913
Mode functions for the effective action 430—1 503—4
Mode functions for “in-in” formalism 666
Mode functions, “in” and “out” mode functions 377ff
Modulation function 199ff
Momentum operator 183ff
Momentum operator and de Rham cohomology 191
Momentum operator, ambiguity in 184
Momentum operator, coordinate transformation law of 187
Momentum operator, position representation of 190ff
Monopole detector 620—1
Morse index 267
Morse index, application to path integration 271
Morse index, generalized Morse index 272ff
Morse index, Morse index theorem 271
Negative dimensional Euclidean spaces 1025—1026
Negative frequency function for boson fields 321
Negative frequency function for fermion fields 367
Negative frequency function for fields in nonstationary backgrounds 393—394
Negative frequency function for “in-in” formalism 669
Nonpolynomial systems 60
Nonrelativistic particle in curved space 252ff
Nonrelativistic particle in flat space 799ff
Nonrelativistic particle in flat space, functional integral for 803
Norm of a super Hilbert space vector 1000
O(1, n-1) see Lorentz group
On shell 13
One-loop approximation to point-to-point amplitude 243
One-loop approximation, WKB (or semiclassical) approximation in general 247ff
One-loop finiteness of quantum gravity 509 788—789
One-particle scattering amplitude 386
One-particle-irreducible graphs 416 701
Operator dynamical equations 168
Orbits 20
Orbits, space of 20
Orientability of the real universe 711
Pair annihilation amplitude 385
Pair production amplitude 384
Pair production by black-hole collapse geometry 654—655
Pair production by constant electric field 741
Particle production by weak backgrounds 586ff
Particle production by weak backgrounds, production of photons 590
Particle production by weak backgrounds, production of scalar particles 589
Particle production by weak backgrounds, production of spinor particles 591
Path integrals 213ff
Path integrals in the covering space 225ff
Path integrals, ambiguity in 219ff
Path integrals, homotopy in 220ff
Path integrals, measure for Lagrangian path integral 217
Path integrals, measure for phase-space path integral 219
Pauli — Villars regularization 866
Peierls bracket 49ff
Peierls bracket, canonical covariance of 708
Peierls bracket, commutes with use of the dynamical equations 50
Peierls bracket, equivalent to Poisson bracket when system is standard canonical 54
Peierls bracket, identities satisfied by 50—51
Perturbative renormalizability 420
Physical observables 25 1002—1003
Pin 346 346
Planck units 625 784
Poincare group 107ff 357ff
Point-to-point amplitude 214
Point-to-point Green’s function 237
Polarization spinors for massive spinor field 891
Polarization spinors for massless spinor field 910
Polarization tensors for massive antisymmetric tensor field 882
Polarization tensors for massive symmetric tensor field 886
Polarization tensors for massless antisymmetric tensor field 971
Polarization tensors for massless symmetric tensor field 908
Polarization vector-spinors for massive spin-3/2 field 899
Polarization vector-spinors for massless spin-3/2 field 917
Polarization vectors for massive vector field 878
Polarization vectors for massless vector field 903—904
Pole operation in renormalization theory 701—702
Polynomial systems 60
Position mapping 179
Position representation 188ff
Positive frequency function for boson fields 321 331
Positive frequency function for fermion fields 367
Positive frequency function for fields in nonstationary backgrounds 391
Positive frequency function for “in-in” formalism 669
Probability amplitude 162
Probability as an emergent concept 208
Probability ensemble interpretation of 153ff
Probability irrational probabilities 150—151
Probability, rational probabilities 149—150
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте





 and
and 

 -function for
-function for 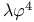 model
model  )
) 