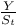|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Цейтен Г.Г. — История математики в 16 и 17 веках |
|
|
 |
| Предметный указатель |
Местлин 34 35
Место 194 206—207 217—218 235
Метод исчерпывания 229 243 248 257 274 284 308 314 438
Метод неопределенных коэфициентов 220 222 339 376—381 386 392—394 423 429 431 439
Механика 242—256 396—413 446—447
Мёрбеке 21
Мидорж 49 50 188
Минимум см. "Максимум и минимум"
Мнимые числа 103-104 122—124 221 240
Моавр 439
Момент инерции 256 310—312
Момент, предложение о моменте 248 284 285 424—425
Монж 202 335
Монтальт см. "Паскаль Б."
Монтукла 335
Наве 20
Наклонная плоскость 250—251 253
Наср-Эддин 125 128 230 358
Неделимые величины 264—268
Независимое переменное 372 373 375 390—391 423 427—429 442
Нейль 64 308
Неморарий см. "Иордан Неморарий"
Непер 13 37 42—43 78 124 143 145—150 154—156 185 277 278 360 364 390
Непрерывность 242—244
Непрерывные дроби 163—165 314—315
Николай Кузанский см. "Кузанский"
Нунец 361
Ньютон 13 18 27 36 55 58 60 61 63—67 68 69—72 73 74—88 92 154 223 234—238 240 241 286 301 314 317 325 358—361 370—416 418—422 424 427 429 430—434 436—439 446—448
Ньютон, анаграммы Н. 71 388 429—431
Ньютон, интерполяционная формула Н. 237
Ньютон, параллелограм Н. 378
Ньютон, предложение о степени 235
Обратные задачи на касательные 422 427—431 435 442 446—447 см.
Объем 249 257—260 267—272 280 303 353
Огибающие 235 331 335 358—359 440
Озанам 157
ОЗУ 307 309
Ольденбург 57 65 70 79—82 381 383 416 424 429
Омар Алхайями 113
Орезм 143 204 205 332 343
Ото 30 128 138
Отрицательные числа 99 102 110 114—115 119 121—123 215 221 240 293 433
Падение 251—254
Падение в сопротивляющейся среде 410—411
Папин 60
Папп 17 22 26 133 191 192 205 217 219 244 245 249 258 263 308 342 343
Параболы высших порядков см. "Квадратуры"
Паскаль Э. 45 52 199 347
Паскаль, арифметический треугольник П. 116 179 183 416
Паскаль, Блэз 13 20 49 51 52—54 55—57 59 61 81 116 168 178—184 186 196—198 200 201 233 235 236 272 279—281 290—291 295 300 302 303 307—309 368 374 376 384 387 416 417 421 422 425
Паскаль, вырезки (onglets) П. 280—281
Паскаль, предложение П. 197
Пачиоло 157 181
Пелль 167 177
Пембертон 78
Персонн см. "Робеваль"
Перспектива 186—202
Пи ( ) 135—136 139 140 293—300 314—316 319—320 384 418 ) 135—136 139 140 293—300 314—316 319—320 384 418
Пикар 34
Пиркгеймер 29
Питиск 30 42 138 152
Плануд 158
Платон 23
Площади как суммы неделимых величин 264—271 см.
Поверхности 2-го порядка 195 209 245
Пожизненная рента 184
Показатели 142—144 215
Показатели беспредельно возрастающие 445
Показатели дробные 143 292—293 301 376—377 432—433
Показатели отрицательные 292 301 376—377 384 433
Показатели, нулевой показатель 143
Показательная функция 380 382 429 441 см.
Полярные координаты см. "Координаты"
Полярный треугольник 125 128
Понселе 196 202
Постоянная интегрирования 369 387 394 407 444
Предел 460—461 438
Предельное значение 441 445
Приближения 312—328 см. "Непрерывные "Ряды"
Приведенная длина маятника 254—256 310
Принцип возможных перемещений 251
Принцип живых сил 60 88 256
Притяжение шаров 407—409
Притяжение, всеобщее 396—398 402—405 407—409
Притяжение, пропорциональное расстояние 405
Проективная геометрия 186—202 233 235—237
Проекция, прямоугольная 186
Проекция, центральная 184—201 236—237
Производные в форме 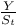 345 350—351 363—370 433 345 350—351 363—370 433
Простаферетрический метод 141—142 155
Пространственные кривые 221 272
Прямоугольные треугольники, с рациональными сторонами 166 169 174—175
Птолемей 17 23 32 127 140 186 358
Птолемей Analemma 140 186
Пуансо 135
Пюжо 195 196
Разности, конечные 238 412 416
Разностные ряды см. "Ряды"
Райт 42 '
Раме см. "Рамус"
Рамус 20 37—38 51
Региомонтан 18 28—29 42 125—128 136 138 156 165
Рекорд 41 115
Ректификация 305—308 353—358 383 395 444
Ремер 34 358
Рен 54 63 68 74 308 353 354 403
Ретик 30 126 128 138 139 152 155
Ризе 27
Риттер 14
Роберваль 45 48—49 51 52 54 77 182 256 265 275 282 283 291 306 310 313 333 385 338 347 352—354 365
Рокк, Антонио 249
Ролль 55 163 342
Роумен 41 132—135
Рудольф (Коссист) 27—28 110 136
Ряды Архимеда 313—314 318 322 324
Ряды для круговых функций 318 382 418 429
Ряды для логарифмической функции 318 320—326 381—382 429—430 439
Ряды для неэлементарных функций 382—384 429—430
Ряды для показательной функции 382—384 429—430
Ряды для тригонометрических функций 382 429
Ряды у Броункера 320—327
Ряды у Галлея 439
Ряды у Грегори 317
Ряды у Иог. Бернулли 442 444—445
Ряды у Лейбница 384 416—419 430
Ряды у Меркатора 325—326 417
Ряды у Ньютона 376—387 392-394 415 429
Ряды у Як. Бернулли 445
Ряды, арифметические 143 340—341 440 445
Ряды, арифметические высших порядков 116 178—179 275 416
Ряды, геометрические 119 143 445
| Ряды, как способ изображения функций 380
Ряды, как средство для интегрирования см. "Диференциальные уравнения" "Интегрирование"
Ряды, обращение рядов 378
Сакери 230
Севиль 42
Сен-Мартэн 168
Сент-Круа 44 168 169 171 173
Сетиш 160
Сила, понятие 396—398
Сила, сложение и разложение сил 250
Символика, алгебраическая 108—116 165 184 202 213—217 221 227 228 230—232 238 301
Символика, инфинитезимальная 232 301 375 389 390 414—415 422—423 425—426 428 431—434 441 446
Символика, логическая 239
Символика, тригонометрическая 110 230 231
Симпсон 65 238
Скорость 252—254 372
Скорость, сложение скоростей 334—335 354 366 398
Скоутен 39 47 57 58—60 222 340 441 348
Слюз 54 57 59 65 208 342 348 350 351
Снеллий 41 129 139 140 361
Соприкасающийся круг 440 см.
Сочетания и перестановка 180 416
Спиноза 79 84
Спираль галилеева 305
Спираль логарифмическая 306 361 364 370 406 440
Спираль параболическая 440
Спираль, архимедова 210 303—306 335
Спираль, спирали высших порядков 304 306
Стевин 40—41 108—111 114 132 136 137 143 212 249—251
Стирлинг 238
Студничка 33
Суммы степеней натуральных чисел 179 275 291
Сходимость 134 314—315 322—327 379—381 384 420 438 445
Табит ибн Курра 170 171
Табличный способ изображения 115—116 128—129
Тавтохронизм 354—355 359 447
Таннери 14
Тарталья 20—21 22 96—101 103 104 106 108 113 116—118 120 122 137 157 179 180 253 295 330
Тела и поверхности вращения 245—246 248—249 257—260 268—270 308—309
Теория вероятностей 180—184 445—446
Теория методы доказательства у Ферма 155—180
Теория предложения Форма 155—178
Теория чисел 156—166
Торричелли 14 25—26 52—54 61 67 251 253 263 271 291 303 306 331 333—335 352—353 361 365 366
Точка перегиба 338 348 396 434 440 443
Траектория 447
Трактриса 446
Трансцендентность 317 419—420 442
Тригонометрические таблицы 126 128—130 138—140
Тригонометрия 124—135 138—142 155 166 230
Тригонометрия, применение к алгебре 129—135
Трисекция угла 94 130—132
Тэйлор 412 445
Убальдо 23 188 189 190 204
Удар 256
Указатели 238
Улуг-Бег 95
Умножение площади на площадь 272 281
Уравнения 3-й степени 94—100 117—122 185 221—223 240 330
Уравнения 3-й степени, неприводимый случай 98—101 103 105 130—131
Уравнения 4-й степени 106—107 117 221—223 240
Уравнения 5-й и высших степеней 223—224 239—240
Уравнения с правой частью, равной нулю 124
Уравнения трехчленные 112 118—120
Уравнения, алгебраические, теория 101—103 117—124 220—221 239—241 342
Уравнения, выражение коэфициентов через корни 120—122
Уравнения, деление круга и угла 116 123—124 130—134 139
Уравнения, исключение неизвестных 203 238 239
Уравнения, неопределенные 1-й степени 156 158—163
Уравнения, неопределенные высших степеней 172—177
Уравнения, образование из множителей 120—124
Уравнения, правило знаков Декарта 221 240
Уравнения, равные корни 102 239 329—330 339—342 440
Уравнения, решение с помощью геометрических построений 129—132 208—209 222—224
Уравнения, суммы степеней корней 122 240
Уравнения, числовое решение 137—138 380—381
Урс, Раймар 141 142
Файль 14 56 246—248
Фаульгабер 28 178
Ферма 13 43 44—45 48—49 51—53 55 56 58 59 62 64 65 81 167—185 199 203—209 211 213 216 217 219—221 224 231 232 234 235 252 268 270 272—279 281—285 289—291 300 302—305 307—310 342—353 357 362 364 368 373 374 376 387 396 418 422 432 434
Ферма, коноид Ф. 305
Ферма, теорема Ф. 171—172
Феррари 22 106—108 117 358
Ферро 20 21 22 96—98 104 108 113 118 120
Финке 31 33—34 38 126 155
Фиоре 20 21 97
Флакк 43
Флюксии высших порядков 390—391 412 415
Флюксии и флюенты 371—372 375 388—396 398—402 411—413 430—431 434 437
Флюксия (символ) 375 388—391 415
Формула Симпсона 238
Формула Стирлинга 238
Формула Тейлора 412
Френикль 44 45 168
Функция, геометрическое изображение 280—281 367 413 442 448
Функция, изображение с помощью длины дуги 444
Функция, изображение с помощью ряда 380 382—384 442
Функция, интегрирование как источник получения новых функций 442
Хаким 140
Цейлен 41 139
Цейтен 23 24 40 46 61 69 75 97 100 115 123 179 186 191 198 204 209 212 232 243 249 250 252 278 279 295 296 299 329 330 346 372 389 397 399 420 426 434 435
Центр тяжести 244—251 285 287—288 303 311—312 349 353 424—425
Центробежная сила 256 403
Цепная линия 361 442 447
Циклоида 254 285 308 309 334 335 337 338 346 351—359 383 419 448
Циклоида, падение по Ц. 355—356 360 407 410
Циклоида, эпи и гипоциклоида 359 396 407
Циссоида 299—300 335
Чирнгауз 79 81 82 84 239—241 358 415 424
Числа, представление в виде суммы, квадратов и т. п. 172—177
Числа, разложение на множители 169—172
Числа, совершенные и дружественные 156 170—171
Числа, фигурные 178—180 416
Шаль 200 210 211
Швентер 29 157 164 165
Штаудт 196
Штейнер 200
Штифель 19 27—28 34 78 105 108 114—116 124 130 137 143—145 165 178 179 295
Штурм 240
Шулер 139
Шюке 37 109 114 143 157 158
Эволюты 356—358 395 396 440 441
Эйлер, Леонардо 91 172 177 239 294 295 299 301
Эйлер, П. 91
Эллиптические функции 383
Энгельс, Ф. 40
Энестрём 14
Эпициклоида см. "Циклоида"
Эратосфэн 243
Юнус см. "Ибн Юнус"
Юшкевич, А. 56
Яков из Шпейера 165
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 )
)