|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Соколов Н.П. — Введение в теорию многомерных матриц |
|
|
 |
| Предметный указатель |
( , ,  , ,  ) ранг многомерной матрицы 79 ) ранг многомерной матрицы 79
( , ,  , ,  )-эквивалентные многомерные матрицы 79 )-эквивалентные многомерные матрицы 79
( , ,  , ,  )-элементарные преобразования многомерной матрицы 76 )-элементарные преобразования многомерной матрицы 76
( , ,  ) показатель многомерной матрицы 137 ) показатель многомерной матрицы 137
( , ,  ) ранг многомерной матрицы 79 ) ранг многомерной матрицы 79
( , ,  ) ранг многомерной полиномиальной матрицы 124 ) ранг многомерной полиномиальной матрицы 124
( , ,  )-ассоциированный пучок матриц 129 )-ассоциированный пучок матриц 129
( , ,  )-инвариантные множители многомерной матрицы 127 )-инвариантные множители многомерной матрицы 127
( , ,  )-инвариантные множители многомерной полиномиальной матрицы 125 )-инвариантные множители многомерной полиномиальной матрицы 125
( , ,  )-минимальные индексы ( )-минимальные индексы ( , ,  )-сингулярного пучка многомерных матриц 133 )-сингулярного пучка многомерных матриц 133
( , ,  )-минимальный полином многомерной матрицы 110 )-минимальный полином многомерной матрицы 110
( , ,  )-нормальная форма многомерной матрицы 128 )-нормальная форма многомерной матрицы 128
( , ,  )-подобные многомерные матрицы 128 )-подобные многомерные матрицы 128
( , ,  )-свернутое произведение многомерных матриц 56 58 )-свернутое произведение многомерных матриц 56 58
( , ,  )-свернутое частное 115 )-свернутое частное 115
( , ,  )-свернутый остаток 115 )-свернутый остаток 115
( , ,  )-свернутый полином от многомерной матрицы 99 )-свернутый полином от многомерной матрицы 99
( , ,  )-характеристический полином многомерной матрицы 102 )-характеристический полином многомерной матрицы 102
( , ,  )-характеристическое уравнение многомерной матрицы 95 )-характеристическое уравнение многомерной матрицы 95
( , ,  )-характеристическое число (собственное значение) многомерной матрицы 93 )-характеристическое число (собственное значение) многомерной матрицы 93
( , ,  )-эквивалентные многомерные матрицы 78 )-эквивалентные многомерные матрицы 78
( , ,  )-эквивалентные многомерные полиномиальные матрицы 123 124 )-эквивалентные многомерные полиномиальные матрицы 123 124
( , ,  )-элементарные делители многомерной матрицы 127 )-элементарные делители многомерной матрицы 127
( , ,  )-элементарные делители многомерной полиномиальной матрицы 126 )-элементарные делители многомерной полиномиальной матрицы 126
( , ,  )-элементарные делители пучка многомерных матриц 130 )-элементарные делители пучка многомерных матриц 130
( , ,  )-элементарные преобразования многомерной полиномиальной матрицы 121 )-элементарные преобразования многомерной полиномиальной матрицы 121
Алгебраическое дополнение 24
Взаимно дополнительные миноры 24
Гипер детерминант 13
Детерминант косигнатурный 14
Детерминант многомерный 16
Детерминант р-мерный 13
Детерминант смешанный 14
Диагональ 7
Диагональ главная 7
Диагональное сечение 7
Диагональное сечение главное 7
Дополнительный минор 23
Индексы альтернативные 13
Индексы кэлиевы 13
Индексы неальтернативные 56
Индексы свободные 56
Индексы скоттовы 56
Канонический вид многомерной матрицы 81
Канонический вид пучка многомерных матриц 132
Квазинормальная форма матрицы 153 168
Квазисобственный вектор 146
Квазистохастически подобные матрицы 154 168
Квазистохастически эквивалентные матрицы 152 167
Квазихарактеристическое уравнение матрицы 147 165
Квазихарактеристическое число 146 163
Кодетерминанты 14
Кодетерминанты союзные 14
Критерий ( , ,  , ,  )-эквивалентности многомерных матриц 78 79 )-эквивалентности многомерных матриц 78 79
Критерий ( , ,  ) подобия многомерных матриц 128 ) подобия многомерных матриц 128
Критерий ( , ,  ) примитивности многомерных матриц 136 ) примитивности многомерных матриц 136
Критерий ( , ,  ) эквивалентности полиномиальных многомерных матриц 125 126 ) эквивалентности полиномиальных многомерных матриц 125 126
Критерий ( , ,  )-неразложимости неотрицательной многомерной матрицы 135 )-неразложимости неотрицательной многомерной матрицы 135
Критерий квазистохастического подобия матриц 154 168
Критерий квазистохастической эквивалентности матриц 152 167
Критерий строгой ( , ,  )-эквивалентности ( )-эквивалентности ( , ,  )-регулярных пучков многомерных матриц 130 )-регулярных пучков многомерных матриц 130
Критерий строгой ( , ,  )-эквивалентности ( )-эквивалентности ( , ,  )-сингулярных пучков многомерных матриц 129 133 )-сингулярных пучков многомерных матриц 129 133
Кронекерово произведение многомерных матриц 69
Матрица  -свернутая 71 -свернутая 71
Матрица 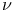 -развернутая 73 -развернутая 73
Матрица ( , ,  , ,  )-ассоциированная 74 )-ассоциированная 74
Матрица ( , ,  )-ассоциированная 75 )-ассоциированная 75
Матрица ( , ,  )-единичная 83 )-единичная 83
Матрица ( , ,  )-неособенная 78 )-неособенная 78
Матрица ( , ,  )-неразложимая 135 )-неразложимая 135
| Матрица ( , ,  )-обратная 85 87 )-обратная 85 87
Матрица ( , ,  )-обратная левая 86 )-обратная левая 86
Матрица ( , ,  )-обратная правая 86 )-обратная правая 86
Матрица ( , ,  )-покрываемонеразложимая 136 )-покрываемонеразложимая 136
Матрица ( , ,  )-примитивная 136 )-примитивная 136
Матрица ( , ,  )-разложимая (полностью или частично) 135 )-разложимая (полностью или частично) 135
Матрица ( , ,  )-симметрическая 75 )-симметрическая 75
Матрица ( , ,  )-собственная 93 )-собственная 93
Матрица ( , ,  )-стохастическая 144 )-стохастическая 144
Матрица ( , ,  )-характеристическая 93 )-характеристическая 93
Матрица дважды квазистохастическая 151 167
Матрица дважды стохастическая 151 167
Матрица диагональная 8
Матрица квазистохастическая 148 165
Матрица квазихарактеристическая 146 163
Матрица клеточно-диагональная 12
Матрица кососимметрическая 9
Матрица кососимметрическая относительно нескольких индексов 9
Матрица минорная 28
Матрица неотрицательная 135
Матрица нулевая 8
Матрица положительная 135
Матрица пространственная 5
Матрица р-мерная 5
Матрица расширенная 5
Матрица с квазиспектром 147
Матрица сжатая 5
Матрица симметрическая 8
Матрица симметрическая относительно нескольких индексов 8
Матрица транспонированная 10
Матрица фундаментальная ( , ,  )-квазисобственная 163 )-квазисобственная 163
Матрица фундаментальная ( , ,  )-собственная 96 )-собственная 96
Минор многомерного детерминанта 23
Нормальная форма полностью ( , ,  )-разложимой неотрицательной многомерной матрицы 142 )-разложимой неотрицательной многомерной матрицы 142
Обобщенная теорема Лапласа 28
Обобщенная формула Бине — Коши 62
Обобщенное детерминантное тождество Дьиреша 40
Обобщенное детерминантное тождество Смита 38
Обобщенное разложение Альбеджиани 51
Общая теорема Безу 121
Общая теорема Гамильтона — Кэли 103
Общая теорема Кронекера 134
Общая теорема Перрона 138
Общая теорема Фробениуса 139
Перманент 14
Полностью свернутое произведение многомерных матриц 67
Правило Кэли — Райса умножения детерминантов 29
Правило Скотта — Райса умножения детерминантов 31
Произведение многомерных матриц без свертывания 65
Пучок многомерных матриц 129
р-матричный полином 114
р-матричный полином ( , ,  )-регулярный 114 )-регулярный 114
Разность многомерных матриц 54
Род детерминанта 13
Сечение (простое или кратное) матрицы 5 6
Сигнатура детерминанта 13
Сложение многомерных матриц 51
Строго ( , ,  )-эквивалентные пучки многомерных матриц 129 )-эквивалентные пучки многомерных матриц 129
Сумма многомерных матриц 51
Теорема Безу 26
Теорема Вандермонда 26
Теорема Коши 27
Теорема Лапласа 26
Тождественно равные матрицы 50
Трансверсаль 7
Трансверсальные сечения матрицы 7
Трансверсальные строки матрицы 7
Трансверсальные элементы матрицы 7
Третье правило составления произведения детерминантов 67
Член детерминанта 13
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 ,
,  ,
,  ) ранг многомерной матрицы
) ранг многомерной матрицы 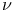 -развернутая
-развернутая