|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Morel J.-M., Solimini S. — Variational Models for Image Segmentation: with seven image processing experiments (Progress in Nonlinear Differential Equations and Their Applications) |
|
|
 |
| Предметный указатель |
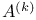 , , 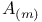 , reflected sets of A 9.1 , reflected sets of A 9.1
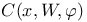 , angular neighbourhood of W (9.68) , angular neighbourhood of W (9.68)
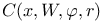 , angular neighbourhood of V at x with angle , angular neighbourhood of V at x with angle  and radius r 12.1 and radius r 12.1
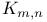 (8.9) (8.9)
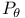 , orthogonal projection onto the hyperplane orthogonal to the direction , orthogonal projection onto the hyperplane orthogonal to the direction  12.3 12.3
 -set 8 preliminary -set 8 preliminary
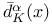 , upper spherical density of K at x 8.2 , upper spherical density of K at x 8.2
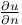 , derivative of u in the direction normal to K 13.1 , derivative of u in the direction normal to K 13.1
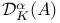 , , 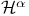 -mean density of K on A 8.1 -mean density of K on A 8.1
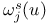 , oscillation of u (14.22) , oscillation of u (14.22)
 -algebra 6.1 -algebra 6.1
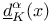 , lower spherical density of K at x 8.2 , lower spherical density of K at x 8.2
 -net 10.1 -net 10.1
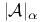 6.1 6.1
1-normal segmentation 5.2
2-normal segmentation 5.2
2.1 sketch 4.1 3.3
2.5 sketch 4.1
Affine invariant (segmentation) 4.5
Ahlfors set 15.5 (15.30)
Almost covering (7.7)
Almost everywhere (a.e.) 8 preliminary
Almost isolated (point of a segmentation) (14.17)
Alvarez — Guichard 2.4
Alvarez — Lions — Morel 2.4
Ambrosio — Tortorelli 4.4
Angular neighbourhood (9.66)
Anisotropic diffusion 2.3
Approximated tangent space (9.20)
Ascoli — Arzela theorem 5.2
B(x, y), cylinder 12.1
Ballester — Caselles — Gonzalez 4.4
Beaulieu — Goldberg 3.3
Besl — Jain 3.1
Blake — Zisserman 4.4
Borel set 6.2
Brice — Fennema 3.3
Brouwer fixed point theorem (11.16)
C(x, y), double cone 12.1
Caratheodory criterion 6.23
Caselles — Catte — Coll — Dibos 3.3
Catte — Coll 2.2
Causality 1.2
Chambolle 4.4
Channel 3.1
Coarea formula 16.2
Cohen — Vinet — Sander — Gagalowicz 3.3
Common boundary of two regions 5.2
Compact metric space 10.1
Complet metric space 10.1
Connected, path connected, connected set with finite Hausdorff measure 6.3
Constrained optimization 3.3
Convergence of 2-normal segmentations 5.6
Convergence of compact sets (10.1)
Convergence of piecewise constant segmentations 5.2
Convergence of rectifiable curves 5.2
Convergence of tangent affine spaces (9.59)
Corners 4.1
Covering 6.1 see
Covering lemma 7 (13.15)
Covering, almost covering (7.7) (11.23)
Covering, disjoint covering (7.1) (7.8) (7.10) (7.12) (7.14)
Curvature of edges 3.2
Curvature of smooth curves 5.2
Curvature, curvature estimate for 2-normal segmentations (5.8)
d(X, Y), Hausdorff distance of two sets 10.1
Denoising 2.4
Densities, 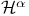 -mean, upper and lower density (8.1) -mean, upper and lower density (8.1)
Densities, conic density (9.68)
Densities, density of the range of a Lipschitz map (11.13)
Densities, lower conic density (of unrectifiable sets) 12 (12.4)
Densities, spherical densities 8.2
Density properties, atomization condition, first and second projection property 15.4
Density properties, essentiality property 15.1
Density properties, uniform concentration property (10.9) 15.4
Density properties, uniform density property 15.2
Differentiability of Lipschitz maps (11.10)
Differentiability of optimal 2-normal segmentations (5.8)
Dual curve lemmas 16.2
EDGE 1.1
Edge (of a 1-normal segmentation) 5.2
Edge growing 3.2
Edge map 4.2
Elliptic equation 13
Enhancement 2.4
Essentiality (of an edge set) (14.17)
Excision lemmas (14.12) (14.15) (14.17)
Excision method (14.1)
Existence of a curve containing the edge set 16.3 16.4
Existence of Mumford — Shah minima, general case (15.44)
Existence of Mumford — Shah minima, piecewise constant case (5.1)
Fubini lemma (12.24) (14.19) (14.43)
Gauss function 2.1
Gestalt psychology 4.1
Golab's theorem (10.19)
Graduated Non Convexity algorithm 4.4
Green formulas 13.2 (13.9) (13.10) (13.13) (13.15)
Haralick 3.3
Haralick — Shapiro 1.1
Harmonic function 13.3
Hausdorff distance 10.1
Hausdorff outer measure 6.1 (6.1)
Heat equation 2.1
Hildreth — Marr 2.1
Hybrid (edge and region growing) method 3.3
I(u), I(K), 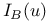 , terms of the Mumford — Shah energy 13.1 , terms of the Mumford — Shah energy 13.1
Illusory contours 1.1
| Image 5.1
Image, Multichannel image 5.1 5.4
Irregular set 6.4 (8.23)
Irregular set, example of (8.30)
Isodiametric inequality 7.3
Isoperimetric inequality 5.2
Jones 3.2
Jordan curve 5.2
Jordan curve lemma (5.2)
Kass — Witkin — Terzopoulos 3.2
Koepfler — Lopez 5.4
Koepfler — Morel — Solimini 5.4
Lebesgue measure 7.3
Leclerc 4.3
Length (of a rectifiable curve, of a segmentation) 5.2
Length, relation between length and Hausdorff measure 11.3
Leonardis — Gupta — Bajcsy 3.1
Lowe 3.2
Lower semicontinuity of Hausdorff measure... 10.4 (10.14)
Lower semicontinuity of the general Mumford — Shah energy (13.6)
Lower semicontinuity of the Mumford — Shah energy for 2-normal segmentations (5.6)
Mallat — Zhong 2.1
Maximum principle (13.5)
Mean curvature motion 2.4
Measurability of sets defined from density properties 8.29
Measurability, (in the sense of Caratheodory) (6.6)
Merging 5.2 5.3
Minimality assumption (M) (14.4)
Minimum description length 4.3
Montaneri — Martelli 3.2
Multiscale edge linking 3.2
Multiscale region growing 3.1
Mumford — Shah 3.1
Negligible set 6.1
Neumann boundary condition (13.1)
Nitzberg — Mumford 4.1
Nitzberg — Shiota 2.2
Nonuniqueness of Mumford — Shah minima (15.49)
Nordstroem 4.4
Osher — Rudin 2.1 2.4
Osher — Sethian 2.3
Outer measure (6.2) (6.3)
Pavlidis 3.3
Pavlidis — Horowitz 3.1
Pavlidis — Liow 3.3
Perkins 1.1
Perona — Malik 2.2
Precompact metric space 10.1
Projection density arguments (9.36) (9.47) (9.53)
Projection property (first and second) 15.4
Projection property of unrectifiable sets (6.36) 12.3
Pyramidal data structure 3.1
Pyramidal segmentation algorithm 5.4
Rectifiability properties, atomized curve property 16.1
Rectifiability properties, concentrated 16.1
Rectifiability properties, quantified nonconnectedness property 16.1
Rectifiable curve 5.2 11.3
Rectifiable,  -rectifiable surface, set 11.1 -rectifiable surface, set 11.1
Rectifiable,  -simply rectifiable curves and sets 11.3 -simply rectifiable curves and sets 11.3
Reflected of a set 9.1
Reflection arguments (for regular sets) (9.4) (9.6)
Reflection lemmas (9.9) (9.14)
Region growing 3.1
Regions 1.1
Regions of a segmentation 5.2
Regions, overlapping regions 4.1
Regular set (8.23)
Regularity of rectifiable sets 11.2 (11.19)
Regularity, equivalence with rectifiability (12.10)
Regularity, regularity of Mumford — Shah minimal edge set 15.4
Relative boundary 5.2
Reliable set (13.12)
Richardson 4.4
Saliency map 4.2
Sard lemma (11.11)
Scale in multiscale analysis 1.2
Scale in piecewise constant segmentation 5.1
Scale space 2.1
Segmentation 1.1
Segmentation as a partition 5.2
Segmentation, affine invariant 4.5
Selective smoothing 2.2
Sha'ashua — Ullman 4.2
Small oscillation covering 14.2
Small oscillation covering lemma 16.1
Snakes method 3.3
Sobolev space 13.1
Split and merge 3.1
T-junctions 4.1
Tangent space to a regular set 9.3 (9.66) (9.68)
Tangent space to the graph of a differentiable map (11.4)
Tangent space, nonexistence for an unrectifiable set (12.9)
Terzopoulos 3.1
Texture density 3.1
Uniformly concentrated sets 10.4
Unrectifiable 6.4
Unrectifiable, purely unrectifiable set 11.1
Variational formulation 2.1
Variational formulation of edge linking methods 3.2
Variational formulation of region growing methods 3.1
Viscosity solution 2.3
Vitali Covering Lemma 7.14
Vitali covering, approximate covering 7.2
Weak membrane model 4.4
Weiss — Boldt 3.2
Witkin — Koenderink 2.1
Zero crossing of laplacian 3.2
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 ,
, 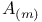 , reflected sets of A
, reflected sets of A 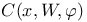 , angular neighbourhood of W
, angular neighbourhood of W 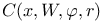 , angular neighbourhood of V at x with angle
, angular neighbourhood of V at x with angle  and radius r
and radius r 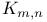
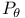 , orthogonal projection onto the hyperplane orthogonal to the direction
, orthogonal projection onto the hyperplane orthogonal to the direction 
 -set
-set 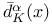 , upper spherical density of K at x
, upper spherical density of K at x 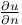 , derivative of u in the direction normal to K
, derivative of u in the direction normal to K 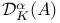 ,
, 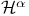 -mean density of K on A
-mean density of K on A 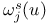 , oscillation of u
, oscillation of u  -algebra
-algebra 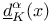 , lower spherical density of K at x
, lower spherical density of K at x  -net
-net 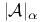
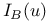 , terms of the Mumford — Shah energy
, terms of the Mumford — Shah energy