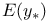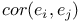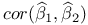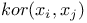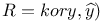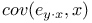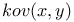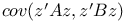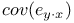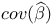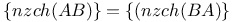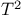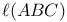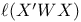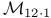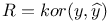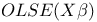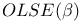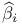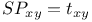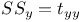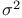|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Isotalo J., Puntanen S — Formulas Useful for Linear Regression Analysis and Related Matrix Theory |
|
|
 |
| Предметный указатель |
Added variable plot 18
Algebraic multiplicity 64
anova 29
Antieigenvalue 48
AR(l)-structure 50 52
Banachiewicz — Schur form 59
Best linear predictor 23
Best linear predictor, BLP(z | Az) 24
Best linear unbiased estimator, 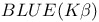 41 41
Best linear unbiased estimator, 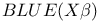 41 41
Best linear unbiased estimator, restricted BLUE 30
Best linear unbiased predictor 52
Bias 22
Block diagonalization 24
Bloomfield — Watson efficiency 49
Canonical correlation 48 67
Cauchy — Schwarz inequality 76
Centered and scaled  3 3
Centered model 9
Centered, 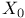 2 2
Centered,  2 2
Centered, y 2
Centering matrix C 2
Cholesky decomposition 70
Coefficient of determination, 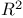 15 15
Collinearity 33
Column space, definition 4
Column space, orthocomplement 4
Condition indexes 33
Condition number 33
Confidence interval for 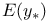 13 13
Confidence interval for 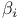 12 12
Confidence interval, Working-Hotelling confidence band 13
Confidence region for 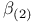 27 27
Confidence region for 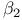 26 26
Consistency of linear model 42
Cook, R. Dennis 24
Cook’s distance 32
Correlation 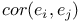 7 7
Correlation 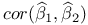 12 12
Correlation 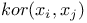 3 3
Correlation 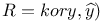 8 8
Correlation as a cosine 3
Correlation matrix 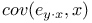 23 23
Correlation matrix 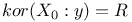 3 3
Correlation matrix 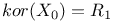 3 3
Correlation matrix 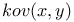 4 4
Correlation matrix cor(x) 5
Correlation matrix, intraclass 56
Correlation, between dichotomous variables 4
Correlation, canonical 48
Correlation, partial correlation 17
Courant — Fischer 65
Covariance 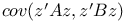 25 25
Covariance adjustment principle 23
Covariance matrix of the prediction error 23 24 69
Covariance matrix, 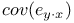 23 23
Covariance matrix, 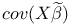 42 42
Covariance matrix, 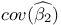 11 11
Covariance matrix, 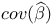 10 10
Covariance matrix, 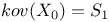 3 3
Covariance matrix, 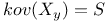 3 3
Covariance matrix, 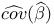 12 12
Covariance matrix, cov(x) 4
Covariance matrix, cov(x, y) 5
Covariance matrix, cov[z — BLP(z | Az)] 24
Covariance matrix, intraclass 57
Covariance matrix, partial covariance 20
Cronbach’s alpha 78
Das Gupta, Somesh 25
Data matrix, 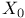 1 1
Data matrix, 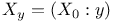 2 2
Data matrix, best rank-k approximation 69
Decomposition, recursive dec. of 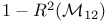 16 16
Decomposition, recursive dec. of 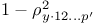 24 24
Disjointness, 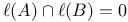 75 75
Durbin — Watson test statistic 51
Eckart — Young Theorem 66 68
Eigenspace 64
Eigenvalue decomposition 67
Eigenvalues, 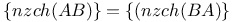 66 66
Equality between OLSE and BLUE 45
Estimability of 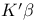 30 30
Estimability of 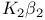 31 31
Estimability of 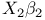 92 31 92 31
Extended (mean-shift) model 31
Fitted values 6
Frisch — Waugh — Lovell Theorem 9 18
Frobenius inequality 74
Full rank decomposition 69
Generalized variance 4 5
Geometric multiplicity 64
Hat matrix H 5
Henderson’s mixed model equations 53
Hotelling’s 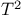 22 22
Inequality, Cauchy — Schwarz 76
Inequality, Frobenius 74
Inequality, Kantorovich 76
Inequality, Samuelson’s 78
Inequality, Sylvester’s 74
Inequality, Wielandt 76
Inertia 72
intercept 8
Interlacing theorem 66
Intraclass, correlation structure 46 56
Intraclass, covariance structure 57
Invariance of 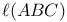 58 58
Invariance of 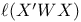 40 40
Invariance of AB — C 58
Invariance of r(AB — C) 58
Invariance of r(X'W — X) 40
Invariance of X'W — X 40
Jordan block 70
Jordan decomposition 70
Kantorovich Inequality 76
Least-squares g-inverse 60
Left singular vector 68
Lehmann — Scheffe theorem 52
Leverage 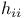 33 33
| Likelihood function 22
Linear Bayes estimator 14
Linear model, definition 1
Linear zero function 41
Linearly complete 51
Linearly minimal sufficient 51
Linearly sufficient 51
Mahalanobis distance, 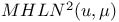 4 21 4 21
Mahalanobis distance, 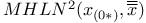 12 12
Marquardt estimator 13
Matrix angle 48
Matrix of corrected sums of squares 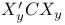 2 2
Matrix, 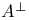 4 74 4 74
Matrix, commutation 79
Matrix, shorted 73
Matrix, triangular factorization 25 70
Maximising, cor(y, b'x) 24
Maximising, var(b'z) 69
Mean squared error 22
Minimising, cov(y — Fx) 23
Minimising, orthogonal distances 69
Minimising, var(y - b'x) 24
Minimum norm g-inverse 60
Minor of A 53
Minus partial ordering 72
Mixed model 53
Model matrix X 1
Multiple correlation in 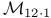 16 16
Multiple correlation in no-intercept model 16
Multiple correlation, 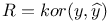 8 8
Multiple correlation, population 24
Multiple correlation, squared 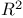 15 15
Mustonen’s measure of multivariate dispersion 24
Normal distribution, conditional 19
Normal distribution, conditional mean 20
Normal distribution, conditional variance 20
Normal distribution, definition 19
Normal equation 7
Normal equation, general solution 7
Null space 4
Observation space 2
Observation vector 2
Ordinary least squares estimator, 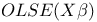 6 6
Ordinary least squares estimator, 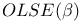 8 8
Ordinary least squares estimator, fitted values 6
Ordinary least squares estimator, restricted OLSE 27
Orthogonal rotation 70
Overall-F value 28
Pandora Box 41 43
Partial correlation, 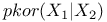 17 17
Partial correlation, 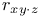 17 17
Partial covariance 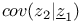 20 20
Poincare separation theorem 65
Polar decomposition 70
Predicted value 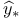 12 12
Prediction error 12
Prediction error, y - BLP(y | x) 19 23 15 25
Prediction interval for 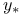 13 13
Principal component analysis, definition 68
Principal component analysis, matrix approximation 69
Principal component analysis, predictive approach 69
Principal component analysis, sample principal components 69
Principal components estimator 13
Principal minor of A 53
Projector,  36 36
Projector, 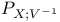 36 36
Projector, C 2
Projector, H 5
Projector, J 2
Projector, M 6
Projector, Schur complement, 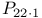 62 62
QR-decomposition 70
Rank cancellation rule 73
Rank-subtractivity partial ordering 72
Reduced model 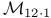 9 9
Regression coefficients 8
Regression coefficients, old ones do not change 9
Regression coefficients, standardized 10
Regression function 20
Regression mean square, MSR 15
Residual mean square, MSE 15
Residual of BLUE 39 44
Residual of OLSE 7 31
Residual sum of squares, SSE 14
Residual, after elimination of 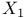 15 15
Residual, externally Studentized 31
Residual, internally Studentized 31
Residual, predicted residual 32
Residual, scaled 31
Ridge estimator 13
Right singular vector 68
Samuelson’s inequality 78
Schur complement 54
Schur’s Triangularization theorem 70
Shorted matrix 73
Shrinkage estimator 13
Shrinkage estimator, Farebrother 14
Shrinkage estimator, Ohtani 14
Shrinkage estimator, Stein 14
Simultaneous diagonalization 66
Singular value decomposition 67
Square root of matrix 70
Standard error of 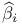 12 12
Sum of products 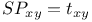 3 3
Sum of squares due to regression, SSR 14
Sum of squares, 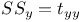 3 3
Sum of squares, change in SSE 15 26 27
Sum of squares, change in SSE(V) 30
Sum of squares, predicted residual 32
Sum of squares, SSE 14
Sum of squares, SSE under 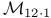 16 16
Sum of squares, SSR 14
Sum of squares, SST 14
Sum of squares, weighted SSE 29 39 44
Sylvester’s inequality 74
Total sum of squares, SST 14
Triangular factorization 25
Triangular matrix 70
Unbiased estimator of 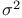 2 15 29 30 44 2 15 29 30 44
Working — Hotelling confidence band 13
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте