|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Okninsky J. — Semigroup algebras |
|
|
 |
| Предметный указатель |
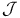 -class 4 -class 4
Algebra, algebraic 155 157 161—163
Algebra, Azumaya 313
Algebra, Azumaya, local-global property for 315
Algebra, fir 205
Algebra, Frobenius 197
Algebra, graded 65
Algebra, graded noetherian 77
Algebra, graded, homogeneous component of 65
Algebra, graded, homogeneous subset of 66
Algebra, graded, left noetherian 77
Algebra, graded, radical of 76
Algebra, graded, strongly 77
Algebra, hereditary 206
Algebra, monomial 39 293—311
Algebra, monomial, graph of 305—310
Algebra, Munn 50
Algebra, Munn, basic ideal of 51—56
Algebra, Munn, induced ideal in 52—55
Algebra, Munn, modules over 55—56
Algebra, Munn, radicals of 55—56
Algebra, of matrix type 48
Algebra, PI- 215
Algebra, right T-nilpotent 170
Algebra, semifir 205
Algebra, semihereditarv 206
Algebra, semilocal 155 159
Algebra, separable 313
Algebra, spectrally bounded 155
Algebra, spectrally finite 155
Algebra, spectrally nondegenerated 155
Algebra, structure matrix of 175 197
Ascending chain condition, on principal ideals 145 288—289 330
Ascending chain condition, on right congruences 142 328—329
Ascending chain condition, on right ideas 135 228 302
Baer condition 187
Bass formula 96
Congruence, determined by an ideal 37
Congruence, determined by the radical 161—162 263—264
Congruence, p-separative 69 169 256—259
Congruence, right 3
Congruence, semilattice 67 290
Congruence, separative 69 169 256—259
Convolution 97
Descending chain conditions 159—178
Descending chain conditions, on principal ideals 15—18 27 171 183 192
Dimension, Gelfand-Kirillov 104—105 223 275—285 296 299—300 304—310
Dimension, Krull 275 286—291 329
Dimension, Krull, classical 275—287 300
Gradation 65 297—298
Gradation, nondegenerated 76 130
Graph, chain in 307
Graph, chain in, simple 307
Graph, cycle in 307
Graph, cycle in, simple 307
Graph, doubly cyclic vertex of 309
Graph, Gelfand-Kirillove dimension of 307
Graph, growth function of 306
Graph, Hilbert series of 308
Graph, right multiplication 302
Group algebra, Azumaya 314—318
Group algebra, hereditary 208—209
Group algebra, PI- 216
Group algebra, regular 180
Group algebra, self-injective 188
Group algebra, semifir 207
Group algebra, semihereditary 209
Group algebra, semilocal 163
Group algebra, skew 73 76
Group, abelian-by-fmite 217 227—228 242—243 286
Group, FC-center of 85 108—116 225 267
Group, finite-by-abelian-by-finite 145 224
Group, fundamental 208
Group, large subset of 90
Group, nilpotent 82 96
Group, nilpotent-by-finite 88 95 98 134
Group, of fractions 68 81 120 224 239 268—270 320
Group, of units 3 40 201 207 318—322
Group, polycyclic-by-finite 77 129—138
Group, polycyclic-by-finite, subsemigroups of 129
Group, quasicyclic 170
Group, unique product 122
Growth 95 223 307
Ideal, determined by a congruence 34
Ideal, prime 54 90 92 216 277—283 286—288 294
Idempotent set 3
Idempotent set, leftp-subset of 165 171
Lattice, 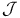 -class 4 -class 4
Lattice, of right congruences 4
Lattice, of right ideals 34 51—53
Module 55—56 74—75
Module, agebraically compact 190
Module, graded 74
Monoid, bicyclic 4
Monoid, conical 206
Monoid, elementary commutative 199
Ore, condition 81
Ore, subset 89 110 116
Quadruple 96
Radical, Brown-McCoy 265
Radical, Jacobson 56 216
Radical, Jacobson, graded 74
Radical, Kurosh-Amitsur 37 39
Radical, prime 55 216
Radical, strongly prime 265
Rank, 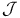 -class 4 -class 4
Rank, of a matrix 8 24—26 243
Rank, of a sandwich matrix 57 241—245
| Rank, of a semigroup 275—291 300 330
Sandwich matrix 6
Sandwich matrix, locally invertible 180
Sandwich matrix, p-equivalent columns of 8 166 171
Sandwich matrix, row p-rank of 245
Sandwich matrix, row p-rank of, strong 245
Semigroup algebra 33
Semigroup algebra, algebraic 157 161—163
Semigroup algebra, artinian 172
Semigroup algebra, augmentation ideal of 35
Semigroup algebra, Azumaya 313—325 332
Semigroup algebra, center of 112—115 318—323
Semigroup algebra, commutative 168 256
Semigroup algebra, contracted 37
Semigroup algebra, fir 206
Semigroup algebra, Frobenius 199—202
Semigroup algebra, hereditary 209
Semigroup algebra, K-separable 324
Semigroup algebra, lattice of ideals of 34
Semigroup algebra, local 169
Semigroup algebra, PI- 213 239 299—304
Semigroup algebra, prime 91 114 294 331
Semigroup algebra, prime PI- 267—273
Semigroup algebra, quasi-Frobenius 196
Semigroup algebra, radical of Jacobson 36 42 121 131—133 160—166 174—177 217 255—266 297—301 329 331
Semigroup algebra, radical of locally nilpotent 132 295
Semigroup algebra, radical of prime 90 133 259—261 286 295
Semigroup algebra, regular 179—186 253 327—328
Semigroup algebra, right chained 170
Semigroup algebra, right fir 207
Semigroup algebra, right noetherian 40 131 135—137 141—151 228 236 302—303 328—329
Semigroup algebra, right perfect 170 193
Semigroup algebra, satisfying a polynomial identity see “PI-”
Semigroup algebra, self-injective 187 328
Semigroup algebra, semifir 207 333
Semigroup algebra, semihereditary 210—211
Semigroup algebra, semilocal 160—168 248 327
Semigroup algebra, semiprimary 172 248
Semigroup algebra, semiprime 91 294
Semigroup algebra, semisimple artinian 173 176 198
Semigroup algebra, with trivial units 121
Semigroup,  -regular 21—28 333 -regular 21—28 333
Semigroup,  -regular, strongly 21 249 -regular, strongly 21 249
Semigroup, 0-cancellative 10 263 286
Semigroup, 0-simple 4 29 229
Semigroup, almost idempotent-free 324
Semigroup, almost weakly nilpotent 88
Semigroup, archimedean components of 67 210 289—290
Semigroup, cancellative 79—138 224—228 239 259 278 318—322
Semigroup, cancellative, FC-center of 108 318—321
Semigroup, center of 3
Semigroup, completely 0-simple 4 6—8 48 92 142—144 146 166—174 181—182 229—234 240—248 268—270 322
Semigroup, completely 0-simple, triangularizable 233
Semigroup, completely semisimple 5
Semigroup, graded 65
Semigroup, idempotent-free 121
Semigroup, inverse 5 60 149 183—185 196 233—236 253
Semigroup, K-complete 257
Semigroup, locally finite 13—17 27 158 174 180—184 222 327
Semigroup, medial 265 291
Semigroup, Nakayama matrix of parameters of 196
Semigroup, nil 10 18—19 26 299
Semigroup, of matrix type 6
Semigroup, of matrix type, row of 6
Semigroup, of matrix units 39
Semigroup, of polynomial growth 95 223 308—309 331
Semigroup, ordered 123
Semigroup, p-separative 69 211 256
Semigroup, periodic 5 157 160 171 180 222
Semigroup, permutative 257—259 284—285
Semigroup, principal factor 4
Semigroup, radical of, locally nilpotent 295
Semigroup, radical of, nil 295
Semigroup, radical of, prime 295
Semigroup, Rees factor 4
Semigroup, regular 5 180
Semigroup, rigid 206
Semigroup, semisimple 5 22 249
Semigroup, separative 67 260
Semigroup, skew linear 8—11 19 25—30 142 250 279—280 333
Semigroup, skew linear, irreducible 10 237 269 271
Semigroup, strongly p-semisimple 60 173 185 196 253
Semigroup, T-nilpotent 18 171
Semigroup, torsion-free commutative 91
Semigroup, unique product 119—128 131
Semigroup, weakly nilpotent 83 98 133
Semigroup, weakly periodic 21—31 149 249—251
Semigroup, with permutational property 221—238 276 279 281 289 299—301 332
Semilattice, of groups 210
Semilattice, of semigroups 67 70 260—261 265
Smash product 71—75
Spectrum 155
Subsemigroup, free 81 93 133—134 304
Subsemigroup, left group-like 41—44
Subsemigroup, of finite index 88
Support 34
Theorem, Amitsur-Levitzki 216
Theorem, Braun 216
Theorem, Grigorchuk 96
Theorem, Gromov 95
Theorem, Kaplansky 216
Theorem, Maschke 173 243
Theorem, Osofcky 193
Theorem, Posner 216
Theorem, Shirshov 222
von Neumann regular element 153
Word, periodic 301
Word, primitive 295—301
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



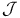 -class
-class  -regular
-regular