|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Dummit D.S., Foote R.M. — Abstract Algebra |
|
|
 |
| Предметный указатель |
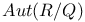 480 480
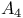 , characters of 618 , characters of 618
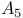 , simplicity of 129 151 , simplicity of 129 151
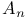 110 110
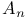 , conjugacy in 132 , conjugacy in 132
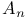 , simplicity of 129 151ff , simplicity of 129 151ff
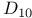 , characters of 612 614 , characters of 612 614
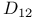 , representation of 632 , representation of 632
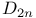 24 24
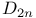 , characters of 602 642 , characters of 602 642
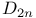 , commutator subgroup 172 , commutator subgroup 172
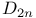 , conjugacy in 133 , conjugacy in 133
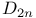 , representations of 576 579 , representations of 576 579
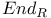 (M) 324 333 360 (M) 324 333 360
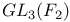 209ff 213 209ff 213
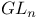 33 236 340 345 33 236 340 345
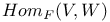 343 343
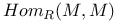 322 322
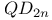 71 87 101 188 493 71 87 101 188 493
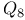 34 69 125 34 69 125
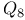 , characters of 602 612 614 617 , characters of 602 612 614 617
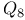 , representations of 576 584 , representations of 576 584
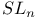 47 104 47 104
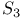 , characters of 608 616 633 , characters of 608 616 633
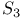 , representations of 598 , representations of 598
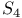 , characters of 609 618 , characters of 609 618
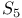 , characters of 619 , characters of 619
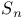 28 28
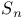 as Galois group 562 as Galois group 562
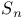 , characters of 613 , characters of 613
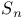 , conjugacy in 126 ff 133 , conjugacy in 126 ff 133
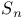 , representations of 575 579 583 584 602 , representations of 575 579 583 584 602
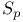 , normalizer of Sylow p-subgroup 133 206 , normalizer of Sylow p-subgroup 133 206
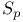 , Sylow p-subgroups of 206 , Sylow p-subgroups of 206
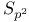 , , Sylow p-subgroups of 189 , , Sylow p-subgroups of 189
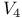 68 68
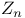 56 56
 427 530 427 530
 -modules 317 323 367 -modules 317 323 367
![$\mathbb{Z}[\sqrt{D}]$](/math_tex/963a713ae10e3cce944331fbd672fa7f82.gif) 232 277ff 287 288 232 277ff 287 288
A.C.C. see “Ascending chain condition”
Abelian extensions of  510ff 514 510ff 514
Abelian group 18 159ff 317
Abelian group, Fundamental Theorem 159ff
Abelian group, representations of 584 585 597
Action group 40 113
Action group, left versus right 130
Affine algebraic set 312
Affine n-space 310 316
Affords, a representation 113 574
Algebra 572
Algebraic closure of finite field 502
Algebraic closures 455ff 502
Algebraic element 432 439
Algebraic extension 432 439
Algebraic integer 622ff
Algebraically closed 311 455 530
Algebraically conjugate characters 613ff
Algebraically independent 559
Algebraically indistinguishable 430
Algorithm for Jordan Canonical Form 408
Algorithm for rational canonical form 393
Alternating function 361
Alternating group 108ff 151ff
Angle, trisecting 446 447
Annihilated by 316
Annihilator, of submodule 371
Annihilators 248 321 360
ansition matrix 346
Artin — Schreier extensions 503 550
Ascending chain condition 288 369
Associate 282
Associative 17
Augmentation ideal 245 255 577
Augmentation map 245
Augmented matrix 349
Automorphism group 39 134ff
Automorphism group of a field 471
Automorphism group of a field extension 471
Automorphism group, 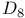 137 137
Automorphism group, 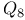 137 137
Automorphism group, 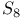 137 137
Automorphism group, cyclic group 136 137
Automorphism group, elementary abelian group 137 323
Automorphism, of a field 468 471
Base field 423
Basis 330 336
Berlekamp’s Factorization Algorithm 503ff
Betti number 159 374
Bijective 2
Binary operation 17
Binary relation 3
Binomial theorem 249
Biquadratic extensions 442 496 503
Biquadratic polynomial 532
Block 118
Boolean ring 231 248 257 270
Building-Up Lemma 338
Burnside’s 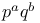 Theorem 198 621ff Theorem 198 621ff
Burnside’s Basis Theorem 201
Burnside’s Lemma 612
Cancellation laws 21
Cardano’s formulas for roots of a cubic 543ff 545
Cardinality 1
Cartesian product 1 643ff
Castelnuevo’s Theorem 560
Casus irreducibilis 547 551
Cauchy’s Theorem 92 95 102
Cayley — Hamilton theorem 390
Cayley’s Theorem 121
Center of group 49
Center of p-group 126 190
Center of ring 231 572 592 596
Central idempotent 333
Central product 158
Centralize 94
centralizer 48
Centralizer of representation 584
Change of basis 346
Character of a group 482 601
Character table 615
Characteristic of a field 422
Characteristic of a ring 249
Characteristic p fields 461
Characteristic polynomial 384
Characteristic subgroup 135 136 139
Chinese remainder theorem 267ff 270 307
Chinese Remainder Theorem for modules 333
Class equation 125
Class field theory 514
Class functions 601 605
Classical Greek Problems 446
Closed 17
Coefficient matrix 349
Cofactor 364
Column rank 345 359
Comaximal ideals 268 280
Commutative 17 18
Commutator 89 170 195ff
Commutator series 197
Commutator subgroup 89 170 195ff 583
Commute, diagram 101
Companion matrix 386
Complement, of subgroup 182 626
Completely reducible module 578 582 591
Composite extensions 505ff
Composites of fields 440ff
Composition factors 103
Composition series 103
Congruence class 8
| Conjugacy class 124 597
Conjugate field elements 487
Conjugate of element 82 124
Conjugate of set 124
Conjugation 43 51
Conjugation in 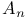 132 132
Conjugation in 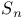 126ff 133 126ff 133
Constituent, of a module 578
Constructibility of the regular n-gon 515ff
Constructible elements 444
Construction of cube roots 447
Construction of the regular 17-gon 516 518ff
Corresponding group actions 130
Coset 77
Coset representatives 77
Cramer’s Rule 363
Cubic equations, formulas for roots 543ff 545
CYCLE 28
Cycle decomposition 28 116
Cycle decomposition algorithm 29
Cycle type 127
Cycle types, of automorphisms 543 553
Cyclic extensions 538 540
Cyclic group 53ff 160
Cyclic group, characters of 615 616
Cyclic group, representations of 575 579 584 599
Cyclic module 327 373
Cyclic subgroup 29
Cyclotomic extensions 464ff 510ff
Cyclotomic fields 451ff 464ff
Cyclotomic polynomial 304 401 465ff 468
Cyclotomy 512
D.C.C. see “Descending chain condition”
Decomposable module 578
Dedekind and Hasse Criterion 281
Degree 1 representations 583 584 601 613
Degree of a field element 433
Degree of a field extension 424 433
Degree of polynomial 234 293
Degree of representation 571 597 603 624
Degree of symmetric group 28
Density of primes 556
Derivative, of a polynomial 306 458
Derived series 197
Descending chain condition 591
Determinant of a matrix 247 360 366
Diagonalizable matrices, criterion 405
Dihedral group 24
Dihedral group as Galois group 558
DIMENSION 335 338
Diophantine equations 245 276
Direct product 19 153ff 158 643
Direct product of modules 329 333 341
Direct product of rings 267
Direct sum 158
Direct sum of modules 329 333 334 341
Direct sum of rings 231
Dirichlet’s Theorem on Primes in Arithmetic Progression 469
Discrete valuation ring 233 260 272
Discriminant 524
Discriminant as resultant 536
Discriminant of 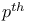 cyclotomic polynomial 536 cyclotomic polynomial 536
Discriminant of a cubic 527
Discriminant of a polynomial 524 533 536
Discriminant of a quadratic 526
Discriminant of a quartic 529
Distributive law 33 225
Divisible group 65 86 590
Division algorithm 5 271
Division ring 226 252 256
Double coset 118
Doubling the cube, impossibility of 446
Doubly transitive 118 613
Dual basis 357
Dual group 168
Dual vector space 357ff
Dual vector space, characters of 609 614 616 633
Dual vector space, representations of 583
Eigenspace 384
Eigenvalue 341 383
Eigenvector 341 383
Eisenstein’s Criterion 303 304
Elementary Abelian group 137 156 317
Elementary Divisor Decomposition Algorithm 407ff
Elementary divisors 162 375
Elementary Jordan matrix 404
Elementary row operations 350 390
Elementary symmetric functions 522
Elliptic function field 566
Embedding of fields 483 489
Endomorphism 324
Endomorphism ring 324
Equivalence class 3
Equivalence relation 3
Equivalent representations 578 602 604
Euclidean algorithm 5 271 274 294
Euclidean Domain 271 279 285 294
Euclidean Domains, modules over 381ff 401ff
Euler  -function 7 269 310 -function 7 269 310
Euler’s theorem 96
Evaluation homomorphism 244 358
Even permutation 108
Exceptional characters 639
Existence of finite fields 462
EXPONENT 167
Exponentials of matrices 415
Expressed by radicals 540
Extension field 423
Extension theorem for isomorphisms of fields 431 454
External direct product 173
F-algebra 572
Factor group 76
Factor through, homomorphism 101
Faithful 42 113
Faithful representation 571 613
Feit — Thompson theorem 104 198 636
Fermat primes 515
Fermat’s Little Theorem 96
Fermat’s Theorem on sums of squares 309
FG-modules 574 580 582
Fiber 2 73
Field 33 226 252 254 422
Field generated by 429
Field of fractions 261ff 281
Finite dimensional 338
Finite extensions 433 434 439
Finite field, existence and uniqueness 462 499
Finite fields 499ff 503
Finitely generated 64 159 220 250 327 436 559 582
First Orthogonality Relation 607 615
Fix, an element 471
Fixed field 473 485
Formal Laurent series 238
Formal power series 238 257 289
Formally real fields 442
Fourier analysis 610
Fractional linear transformations 480 560
Frattini subgroup 201
Frattini’s Argument 195
Free Abelian group 159 223 332
Free generators 220
Free groups 216ff
Free module 316 330
Free nilpotent group 223
Free rank, of a module 374
Frobenius group 170 552 556 557 633
Frobenius group as Galois group 552 557 558
Frobenius group, characters of 633 641
Frobenius kernel 633
Frobenius map 461 468 469 479 499 518
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



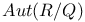
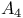 , characters of
, characters of 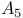 , simplicity of
, simplicity of 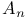
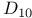 , characters of
, characters of 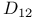 , representation of
, representation of 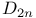
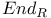 (M)
(M) 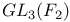
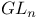
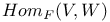
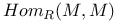
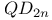
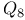
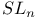
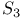 , characters of
, characters of 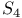 , characters of
, characters of 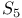 , characters of
, characters of 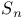
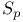 , normalizer of Sylow p-subgroup
, normalizer of Sylow p-subgroup 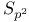 , , Sylow p-subgroups of
, , Sylow p-subgroups of 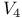
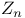

 -modules
-modules ![$\mathbb{Z}[\sqrt{D}]$](/math_tex/963a713ae10e3cce944331fbd672fa7f82.gif)

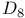
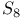
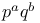 Theorem
Theorem 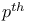 cyclotomic polynomial
cyclotomic polynomial  -function
-function