|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Brualdi R.A., Ryser H.J. Ч Combinatorial Matrix Theory |
|
|
 |
| ѕредметный указатель |
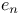 145 145
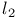 -norm 213Ч214 -norm 213Ч214
Acyclic digraph 335 340 343
Adjacency matrix 25 48Ч52 53 179 317
Adjacency matrix, formal 317Ч323 324
Adjacency matrix, isomorphic 157
Adjacency matrix, regular 157 160
Adjacency matrix, tree 343
Adjugate 301
Admittance matrix 30 see
Affine plane 278Ч80
Affine plane, order of 280
Amitsur Ч Levitzki theorem 331Ч334
ARC 53
Arc, back arc 98
Arc, capacity of 164
Arc, cross arc 98
Arc, dominant 89Ч90
Arc, forest arc 98
Arc, forward arc 98
Arc, weight of 291Ч292
Bipartite graph 44 107Ч144 178 317
Bipartite graph, adjacency matrix of 44
Bipartite graph, bipartition of 44 107
Bipartite graph, complete 108 135 147 148 162:
Bipartite graph, complete, line graph of 153
Bipartite graph, elementary 124
Birkhoffs theorem 9
BLOCKS 278
Branch 62 63
Cayley table 250Ч251 254Ч255 258 262 268 271
Cayley Ч Hamilton theorem 327Ч329 333
Chain 25 210
Chain, directed 54
Chain, length of 210
Chain, weight of 211 212
Characteristic polynomial 26 28 36 76Ч77 88 328Ч329
Chromatic index 51
Circuit 54
Circulant matrix 158Ч162 233
Circulation 168Ч169
Co-term rank 125Ч126 134
Cocktail party graph 36Ч37
Column-linear set 139
Complete digraph 291
Complete graph 23 26 39 318
Complete graph, line graph of 152
Complete graph, spectrum of 28
Complete mapping 251
Completely reducible matrix 76
Complexity (of a graph) 38Ч40 324
composition 191 196
Conference graph 151 155
Conference matrix 154
Configuration 3 20 293 306 307Ч308
Configuration, complementary 305
Configuration, dual 4 12
Configuration, isomorphic 4
Conjugate partition 193 340
Connectivity, algebraic 40Ч53
Connectivity, edge 41
Connectivity, vertex 41
Contraction 62 242
Convex closure 193Ч195
Convex sequence 192 340
Cospectral graphs 26Ч27 155
Cover (of digraph) 134
Covering sequence 190Ч196
Cut 166
Cut, capacity of 166
CYCLE 25
Cycle graph 28
Cycle hypergraph 144
Cycle, directed 54
Cyclic components 71
Cyclic components, computation of 103Ч105
Cyclic matrix 77
Decision problem 245Ч248
Decision problem, polynomial reducible 246
Decision problem, size of 245
Decomposition 251
Decomposition theorems 108 125Ч136 184Ч188
Degree of vertex 24
demand 169
Depth-first number 97
Depth-first search 97
Derangement number Dk 17 222Ч223 233
Derangements 201Ч202 285
Determinant 8 15 16 21Ч22 76 89 90 92 93 94 95 134 209Ч214 235Ч48 291Ч293 294 295 296Ч297 298Ч299 301 309Ч310 311 313Ч314 314Ч316 319 323 325Ч326
Determinantal divisor 337
Diagonal 112
Diagonal structure (hypergraph) 136Ч144
Diagonal structure (hypergraph), isomorphism of 136Ч137
Diagonal structure (hypergraph), partial transposition 142Ч143
Diagonal structure (hypergraph), permutation 140
Diagonal structure (hypergraph), transposition 140
Difference sequence 191 195Ч196 338 339Ч340
Digraph (directed graph) 53 243
Digraph (directed graph), adjacency matrix of 53
Digraph (directed graph), capacity function 164
Digraph (directed graph), characteristic polynomial 88
Digraph (directed graph), condensation 56
Digraph (directed graph), cyclically r-partite 70
Digraph (directed graph), general 53
Digraph (directed graph), girth of 93
Digraph (directed graph), imprimitive 68Ч69
Digraph (directed graph), indegree sequence 173 176
Digraph (directed graph), minimally strong 61Ч68
Digraph (directed graph), out degree sequence 173 176
Digraph (directed graph), primitive 68
Digraph (directed graph), regular 53
Digraph (directed graph), spanning subdigraph 97
Digraph (directed graph), spectrum 88
Digraph (directed graph), splitting of 244
Digraph (directed graph), strongly connected 54 55Ч61
Digraph (directed graph), vertex-weighted 89Ч90
Directed cycle, dominant 90
Directed cycle, weight of 243
Directed forest 96Ч99
Directed forest, spanning 97
Divisor sequence 337Ч338 339Ч340
Doubly stochastic matrix 9 11 117
EDGE 23
Edge coloring 50
Edge, endpoints 23
Eigenvalue inclusion regions 89Ч95
Eigenvalues 16 26 27 76Ч77 88Ч96 130Ч132 145 146
Elementary divisors 337
Elementary similarity 341
Essential column 110
Essential line 110
Essential row 110
Euler  -function 21Ч22 -function 21Ч22
Euler conjecture 275 282Ч283
Eulerian matrix 31
Eulerian trail 332
Evans conjecture 263Ч267
Even digraph 243Ч244
EXPONENT 78Ч87 83Ч85 117
Exponent, gaps 84
Factor 48
Ferrers matrix 206Ч207 208 217
Flow (network) 164Ч171
Flow (network), supply-demand 169Ч171
Flow (network), value of 165
Forest 178
Friendship theorem 151
Frobenius normal form 58 96Ч102
Frobenius normal form, computation of 96Ч106
Frobenius Ч Schur index 72 81
| Fully indecomposable components 115 140Ч141 297
Fully indecomposable matrix 110Ч118 124 228Ч233 296Ч297 299 303
Fully indecomposable matrix, inductive structure 116
Fundamental trace identity 327 329Ч331
Gale Ч Ryser Theorem 176
Galois affine plane 279 280
General digraph 53
Generalized matrix function 295
Generic matrix 294Ч297
Generic nilpotent matrix 335Ч343
Generic skew-symmetric matric 317
Gersgorin's theorem 88
Graph (general) 23 24
Graph (general), adjacent 23
Graph (general), complement 23
Graph (general), complete 23 26
Graph (general), complete multipartite 147 155
Graph (general), connected 27
Graph (general), connected components 27
Graph (general), cospectral 26Ч27 155
Graph (general), cubic 24 37
Graph (general), decomposition of 108 109
Graph (general), degree sequence 179 183
Graph (general), diameter 27
Graph (general), disconnected 27
Graph (general), distance 27
Graph (general), edge 23
Graph (general), induced 23
Graph (general), isolated 23
Graph (general), isomorphic 23 25 26
Graph (general), multiplicity of 24
Graph (general), order 23
Graph (general), regular 24 37 43
Graph (general), simple 23
Graph (general), spanning 23 30
Graph (general), spectrum of 28
Graph (general), subgraph 23
Graph (general), vertices 23
Hadamard product 294 317
Hadamard's determinant inequality 214
Hall's theorem 299Ч301
Hamilton cycle problem 245Ч246 247
Helly type theorem 19Ч20
Hoffman polynomial 147 157 162
Hoffman Ч Singleton graph 154
Horizontal line 277
Imprimitive matrix 70
Incidence matrix 3 29 35 230 304 306
Incidence matrix, formal 293Ч303
Incidence matrix, oriented 29 38
Incidence matrix, weighted 210Ч214
INDEX 103Ч105
Index of imprimitivity 68Ч78
Index of imprimitivity, computation of 103Ч105
Integer sequences 191Ч195
Intersection matrix 11Ч12
Intersection matrix, formal 304Ч310
Intersection matrix, symmetric 305 306 309
Invariant factors 337
Irreducible components 58
Irreducible components, computation of 96Ч106
Irreducible matrix 55Ч61 113 145 297Ч300
Irreducible matrix, inductive structure 67Ч68
Jacobi's identity 321Ч322 301
Join 192
Jordan block 336 340Ч343
Jordan canonical form 335Ч337 340Ч343
Jordan partition 336 338 339Ч340 343
Jordan partition, length of 336
K-decomposition 187
k-path 336Ч337 338
k-path number 336Ч337
k-subset 203
Koenig's Theorem 6 9 44 47 125 128 196 300 301Ч303
Laplacian matrix 30 38 41 325
Laplacian matrix, formal 324Ч327
Latin rectangle 250Ч253
Latin rectangle, completion of 260Ч262 68
Latin square 250Ч290
Latin square, completion of 259Ч262
Latin square, embedding of 262Ч263
Latin square, enlargement of 265Ч267
Latin square, equivalent 253
Latin square, horizontal line of 270
Latin square, idempotent 281Ч283 283Ч284
Latin square, latin line of 270 277
Latin square, mutually orthogonal 272Ч275 286Ч287
Latin square, normalized 250
Latin square, number of 284Ч285
Latin square, partial 259Ч269
Latin square, partitioning of 262Ч263
Latin square, self-orthogonal 287Ч288 289
Latin square, symmetric 251 268 269 283
Latin square, vertical line of 270
Lattice graph 153
Line 1 252 277 278
Line cover 6 110Ч112
Line graph 35Ч37
Line graph, spectrum of 35
Linear set 139
Linearizable set 143 144
Lowlink 100Ч101
MacMahon's master theorem 310Ч316
MacNeish's conjecture 275 282Ч283
Majorization 175
Matching 44Ч52 112 189
Matching sequence 189Ч196
Matching, in digraph 134
Matching, perfect 48
Matrix 1
Matrix, back diagonal of 263
Matrix, column sum vector 172
Matrix, complement of 3 12
Matrix, cover of 6
Matrix, cyclic 70
Matrix, cyclic components 71
Matrix, diagonally dominant 89
Matrix, elementwise product 236
Matrix, existence theorems for 172Ч184
Matrix, line of 1
Matrix, number of l's 123
Matrix, permutation 1
Matrix, principal 17
Matrix, proper cover of 6
Matrix, row sum vector 172
Matrix, submatrix of 17
Matrix, sum of elements of 185
Matrix, triangle of 18
Matrix, upper triangular 338Ч339
Matrix-tree theorem 325Ч326
Matroid, regular 31Ч34
Matroid, unimodular 31Ч34
Max flow-mincut theorem 166Ч168
Meet 192
Menage numbers 202Ч203 204Ч205 233 234 285
Minimax theorem 6
Mixed matrix 303
Moore graph 153
Moore graph, generalized 154
Multicolored graph 131Ч132
Multiedge 24
Multigraph 23
n-set 3
Nearly decomposable matrix 118Ч124 228
Nearly decomposable matrix, inductive structure 120Ч121
Nearly decomposable matrix, number of l's of 122
Nearly reducible matrix 61Ч68 118 124
Nearly reducible matrix, inductive structure 64
Nearly reducible matrix, number of, 1's of 66
Net 277Ч280
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



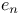
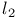 -norm
-norm  -function
-function