|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Niven I., Zuckerman H.S. — An Introduction to the Theory of Numbers |
|
|
 |
| Предметный указатель |
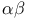 theorem 232 235 theorem 232 235
Abelian groups 53
Additive groups 55
Algebraic integer 178 186
Algebraic numbers 177
Algebraic numbers, closure properties 179 180
Algebraic numbers, degree of 178
Algebraic numbers, field of 181
Algebraic numbers, minimal equation 178
Algorithm 4
Algorithm, Euclidean 7
Approximation by rationals 131 143 148
Artin, E. 238
Associate 186
Asymptotic density 222
Belonging to exponent 48 60
Bertrand's postulate 171
Binary operation 52
Binary quadratic form 116
Canonical form, factorization 14
Cassels, J.W.S. 237
Chinese remainder theorem 31
Common divisor 4
Common divisor of polynomials 174
Common multiple 8
Commutative group 53
Complete residue system 22 55
Composite number 10
Congruence 20
Congruence, degree of 29
Congruence, degree two, prime modulus 47
Congruence, identical 29
Congruence, number of solutions 28 46
Congruence, number of solutions, 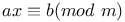 24 29 24 29
Congruence, number of solutions, 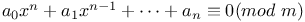 28 38 28 38
Congruence, number of solutions, 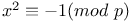 25 25
Congruence, number of solutions, 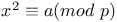 50 50
Congruence, number of solutions, 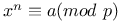 48 48
Congruence, number of solutions, prime modulus 44
Congruence, number of solutions, prime power modulus 40
Conjugate numbers 184
Continued fraction 134
Continued fraction, convergents of 140
Continued fraction, finite 137
Continued fraction, infinite 140
Continued fraction, periodic 152
Continued fraction, simple 135
Convergent 140
Convergent, secondary 148
Coprime 6
Cubic residue 51
Cyclic group 59
Davenport, H. 237
Definite form 116
Degree of a congruence 29
Degree of a polynomial 173
Degree of an algebraic number 178
density 222
Density of square-free integers 226
Density, 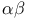 theorem 232 235 theorem 232 235
Density, asymptotic 222
Density, natural 222
Density, Schnirelmann 231
Density, sets of density zero 228
Descent, proof by 101
Dickson, L. E. 237
Diophantine equations 94
Diophantine equations, 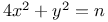 110 110
Diophantine equations, 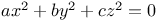 113 113
Diophantine equations, 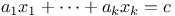 95 95
Diophantine equations, 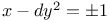 159 159
Diophantine equations, 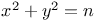 106 106
Diophantine equations, 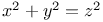 97 97
Diophantine equations, 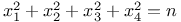 102 102
Diophantine equations, 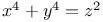 99 99
Diophantine equations, 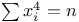 105 105
Diophantine equations, ax + by = c 95
Dirichlet's theorem 19
Discriminant 117
Divisibility 3
Divisibility of algebraic integers 186
Divisibility of polynomials 173
Division algorithm 3
divisors 3
Divisors, sum of 83
Dyson, F.J. 238
Empty sums and products 35
Equivalent quadratic forms 120 121
Eratosthenes, sieve of 17
Euclid's theorem 15
Euclidean algorithm 7
Euclidean quadratic fields 192
Euler's  -function 23 34 88 230 -function 23 34 88 230
Euler's formula 208
Euler's Generalization of Fermat's Theorem 23
Factorial 79
Factorial, power of prime in 79
Factorization, unique 11 13 192
Farey sequence 128
Fermat's last theorem 102
Fermat's method of infinite descent 101
Fermat's theorem 23 26 60
Fibonacci numbers 92
Field 60 181
FORM 116
Function, recurrence 90
Functions, 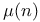 87 225 87 225
Functions,  23 34 88 23 34 88
Functions, 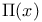 15 164 15 164
Functions,  83 85 212 83 85 212
Functions, 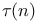 83 85 224 83 85 224
Functions, p(n) 200 211
Functions, [x] 65 78
Fundamental Theorem of Arithmetic 13
Gauss's lemma 65
Gauss's polynomial lemma 176
Gaussian integers 189
Gaussian primes 198
Generating functions 204
Generator 59
Graph 202
Greatest common divisor 4
Greatest common divisor of polynomials 175
Greatest common divisor, Euclidean algorithm 7
Greatest integer function 65 78
Group 53
Group generator 59
Group isomorphism 55
Group, abelian 53
Group, commutative 53
Group, cyclic 59
Group, finite 53
Group, infinite 53
Group, order of 53
Group, order of an element 59
Hardy, G.H. 237
Heaslet, M.H. 237
Hurwitz' theorem 149
Idempotent 63
Identical congruence 29
Identity element 53
Indefinite form 116
INDEX 49
Infinite continued fraction 140 143
Infinite descent 101
Infinitude of primes 15
| INTEGER 1
Integer, algebraic 178 186
Integer, Gaussian 189
Integer, quadratic 187
Inverse element 53
Inversion formula 87
Irrational number, expansion of 141
Irrationality of e 83
Irreducible polynomial 175
Isomorphism 55 183
Jacobi symbol 71
Jacobi's formula 214
Jones, B.W. 237
Le Veque, W.L. 237
Least common multiple 8
Legendre symbol 64
Legendre's Theorem 113
Lehmer, D.H. 237
Lehmer, D.N. 238
Lemma of Gauss 65
Lemma of Gauss on polynomials 176
Magic square 34
Mann's theorem 232 238
Mann, H.B. 232 238
Mathematical induction 2
Minimal equation 178
Modulus 20
Moebius function 87
Moebius inversion formula 87
Monic polynomial 173
Mordell, L.J. 238
Multiple 3
Multiplicative function 84
Multiplicative group 57
Nagell, T. 237
Natural density 222
Natural number 1
Negative form 116
Niven, I. 237
Nonresidue 64
Norm 12 188
Notation see "Symbols"
nth power residues 48
Number, algebraic 177
Number, perfect 86
Number, prime 1
Numerical function 83
Order of an element 59
Ore, O. 237
Parity 9
Partial quotient 135
Partitions 200
Partitions, divisibility properties 220
Pell's equation 158
Perfect number 86
Periodic continued fraction 152
Pollard, H. 238
Polynomial congruence 182
Polynomials over the rationals 173
Polynomials, irreducible 175
Polynomials, monic 173
Polynomials, primitive 176
Positive form 116
Power residue 48
Prime number theorem 15
Prime, relatively 6
PRIMES 1 10 111 164
Primes in arithmetic progression 19
Primes in quadratic fields 191 195
Primes, contained in factorial 79
Primes, distribution of 15 164
Primes, Gaussian 198
Primes, infinite number of 15
Primitive polynomial 176
Primitive root 49 60
Primitive solution 99
Pythagorean triple 100
Quadratic field 187
Quadratic forms 116
Quadratic forms, equivalent 120 121
Quadratic forms, reduced 122
Quadratic irrationals 152
Quadratic irrationals, expansion of 141
Quadratic nonresidue 64
Quadratic reciprocity 68 73
Quadratic residue 64
Ramanujan, S. 238
Rational approximation 131
Rational integer 179
Reciprocity, quadratic 68 73
Recurrence function 90
Reduced quadratic form 122
Reduced residue system 22 57
Relatively prime 6
Relatively prime in pairs 6
Remainder theorem 31
Representation by quadratic forms 116
Residue 22
Residue, quadratic 64
Residue, system, complete 22 55
Residue, system, complete, reduced 22 57
Ring 60
Scherk, P. 238
Schnirelmann density 231
Secondary convergent 148
Sieve of Eratosthenes 17
Simple continued fraction 134 135
Skolem, Th. 238
Square-free 15
Square-free, integers, density 226
Subgroup 61
Sum of four squares 102
Sum of fourth powers 105
Sum of two squares 106
Symbols,  140 140
Symbols,  135 135
Symbols, 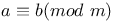 , , 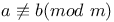 20 20
Symbols, 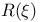 181 181
Symbols, ![$[a_{1}, a_{2}, \cdots, a_{n}]$](/math_tex/ad00b3173ec2a633a6fe7b324f863f1582.gif) 8 8
Symbols, 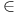 , , 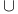 , , 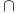 221 221
Symbols, 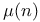 87 87
Symbols, 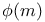 23 23
Symbols, 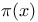 15 164 15 164
Symbols, 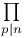 , , 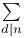 35 35
Symbols,  83 83
Symbols,  121 121
Symbols, 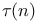 83 83
Symbols, 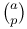 64 64
Symbols, 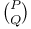 71 71
Symbols, (b, c), 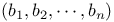 4 4
Symbols, a|b, 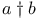 , , 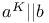 3 3
Symbols, p(n), 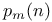 , , 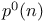 , , 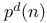 , , 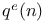 , , 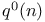 200 200
Symbols, [x] 65 78
Totally multiplicative function 84
Totient 23 34
Unique factorization 11 13
Unique factorization in quadratic fields 192
UNIT 186 190
Universal form 117
Uspensky, J.V. 237
Vandiver, H.S. 238
Vinogradov, I.M. 237
Waring's problem 104
Wilson's theorem 24
Wright, E.M. 237
Zero element 60
Zero form 116
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



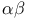 theorem
theorem 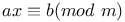
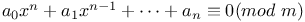
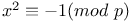
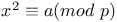
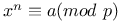
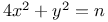
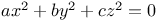
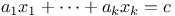
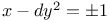
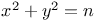
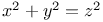
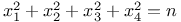
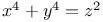
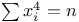
 -function
-function 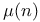

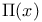

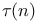


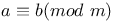 ,
, 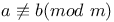
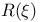
![$[a_{1}, a_{2}, \cdots, a_{n}]$](/math_tex/ad00b3173ec2a633a6fe7b324f863f1582.gif)
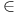 ,
, 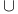 ,
, 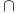
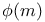
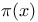
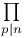 ,
, 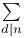

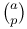
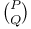
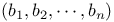
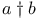 ,
, 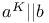
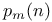 ,
, 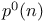 ,
, 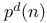 ,
, 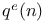 ,
,