Авторизация
Поиск по указателям
Cohn P.M. — Free Rings and Their Relations (London Mathematical Society Monographs)
Обсудите книгу на научном форуме Нашли опечатку?
Название: Free Rings and Their Relations (London Mathematical Society Monographs)Автор: Cohn P.M. Аннотация: In the development of ring theory there are two strands, each with its own problems and methods, and although with many points of contact, they have never merged completely. One of them is the theory of algebras; this was a non-commutative (indeed sometimes even non-associative) theory from the beginning but there were always heavy finiteness restrictions, which are only gradually being relaxed. Thus while there is a fairly substantial theory of Artinian rings, the theory of Noetherian rings is still in its early stages, and although it is being developed vigorously, it is clear that some type of maximum condition is essential for its development.
Язык: Рубрика: Математика /Серия: Сделано в холле Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Издание: 2nd editionГод издания: 1985Количество страниц: 608Добавлена в каталог: 15.05.2011Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Linear automorphism 342 Linear differential operator 191 506 Linearization by enlargement 272 Link in a lattice 180 Local homomorphism 388 Local rank 255 Local ring (scalar, matrix) 22 localization 37 81 390 Localization theorems 457ff. 472 484 Locally free module 48 Lower multiplicative set 382 Lower segment 211 333 Magnus'theorem 296 Makar — Limanov — Czerniakiewicz theorem 355 379 Malcev conditions 35 82 Malcev — Neumann construction 528 Malcolmson's criterion 485 Matrix (pre-) ideal 396ff. Matrix algebraic 220 Matrix basis 1 Matrix local ring 22 Matrix object 463 Matrix reduction functor, 147f. 152 Maximal code 325 Meet 540 Meta (semi-) fir 70 73 Metro-equation 515 Minimal admissible matrix 428 Minimal factorization 248 Mixed free algebra 62 Modular lattice, law 540 Monic matrix over a free algebra 272 Monomial 60 Monomial term 105 Monomorphism 545 Morita equivalence 4 62 78 Multiplicative set 382 Nagata's formula 364 Nagata's theorem 157 Nakayama's lemma 21 Natural isomorphism, transformation 548 Negative module, Neg 236 297 Noetherian ring = ring with (left, right) ACC 15 Non-singular matrix xix Normal closure 443 Normal form in a free algebra 59 Normalizes 443 Null matrix 3 Nullity 161 Numerator 384 One-sided fir 142 176 536 Opposite category 544 Order 55 60 421 Ordered series ring 527 Ore condition, domain 38 Ore set 35 Outer derivation 40 Outer rank 252 Parallelogram law 541 Partition lemma 67 Persistent property 205 442 Perspective 541 Place permutation 364 Polycyclic module 244 Pontryagin's theorem 297 Pos = category of finite partially ordered sets 211 Positive module, Pos 236 297 Power series D-ring 61 Preadditive category 545 Prefix set, code 324 Presentation 552 Primal ring 252 Primary decomposition 184 Primary element 191 Prime 449 Prime element 154 156 Prime matrix 160 425 Prime matrix ideal 401 Prime module 236 Principal ideal domain, ring, PID 71 Principal valuation ring, PVR 130 173 Product of matrix ideals 400 Projective dimension 551 Projective free ring 17 63 Projective module 10 549 Projective trivial ring 18 Projective, in a lattice 541 Proper factorization 268 Proper matrix relation 161 266 Proper specialization 393 Protorsion module 239 Pseudo-Sylvester domain 263 297 418 Pseudo-valuation 95 Pseudolinear extension 517 Pseudolinear mapping 503 Pullback 545 Pure extension 518 Pure subalgebra 341 Pushout 545 PVR = principal valuation ring 130 173 Quasi-Frobenius ring 304 Quasi-identities 414 419 486 Quasi-variety 419 486 Quaternions 23 93 158 225f. 514 Quotient monoid 154 R-field (universal) 388f. Radical of a matrix ideal 402 Radical of a matrix ideal, Jacobson 20 171 Radical of a matrix ideal, tertiary 321 Rank formula (modules over semifirs) 68 Rank of a free algebra 60 Rank of a free module 6 Rank of a matrix 245ff. 424 431 Rank of a module 48 251 Rational closure 382 Rational power series 134 Rational section 487 Rationality criterion 526 Reduced admissible matrix 429 Refinement of a factorization 178 Regular xix Regularly embedded 330 Relation (n-term, trivial) 64 100 Relevant N-value 460 Resolution (injective, projective) 258 551 Retract of a ring 70 221 Right invariant 203 301 Rigid domain, UFD 170 192 Rigid element 41 170 Rigid factorization 190 Rigid monoid 41 Ring of fractions 37 Ringlike matrix object 463 Ringoid 86 545 Root 323 339 Row rank 247 S-ring 263 418 Saturated set, saturation 394 467 SAut, Special automorphism group 357 Schanuel's lemma 24f. 192 552 Schreier refinement theorem 178 542 Schreier — Lewin formula 109 334 Schreierset 333 Schur's lemma 167 222 Section, global (integral, rational) 487 Segment (lower, upper) 211 Semi-Artinian, -Noetherian 195 Semifir 67 85 Semifree module 48 Semihereditary (left, right, weakly) 11 13 63 Semilinear mapping 503 Semiprime matrix ideal 402 Semisimple Artinian ring 193 550 Shear 342 Similar elements, matrices, 25 162 192 Similar right ideals 158 Simple N-value 450 Simple, 167 Singular kernel 391 Singular matrix xix Singularity support 286 410 Skew formal Laurent series 522f. Skew Laurent polynomial 54 Skew polynomial ring 52 497ff. Skew polynomial ring, iterated 532 Skew rational function field 53 521 Source 544 Spacial module 254 Special automorphism 357 Specialization 388 Specialization lemma 285 297 Spectral space 412 Spectrum of a matrix 510 Split exact 549 Squarefree module 196 Stabilize, stab 342 Stable atom 17 Stable GL 449 Stable rank 261 Stably associated 26 63 162 Stably free 15 Stably full 262 Stably honest 418 Standard basis in 3 Standard form in 115f. Strictly bordered 426 Strictly cyclic module 192 Strong DFL-property 201 299f. Strong G-ring, 76 Strong prime ideal 177 Strongly regular 419 Subdirect product 544 Subdirectly irreducible 544 Suffix set 324 Support 59 354 526 Sylvester domain 253 297 417 Sylvester's law of nullity 253 297 Tame automorphism 343 TARGET 544 Tensor D-ring (on a D-bimodule) 61 Tensor product of modules 552 Tertiary radical 321 Test module 192 Three-by-three lemma 547 Top component 344 Topological fir 128 Torsion class, torsion free class 228 296 Torsion element, submodule 46 Torsion free module 46 Torsion module (over semifir) 164 239 297 Total divisor 489 Totally coprime 315 435 Totally inert 84 Totally unbounded 316 Trace form 372 Transcendental matrix 506 Transduction 105 Transfinite degree function 139 Transfinite division algorithm 90 Transfinite weak algorithm 139 152 Translation 342 Transpose of a module, Tr(-) 233 297 Transvection 74 TREE 349 Trivial filtration 95 Trivial operation 405 422 469 Trivial relation 64 475 Trivializable 65 101 475 Truncated filtered ring 111 U(R) = group of units of R xviii UF-monoid 153f. UFD = unique factorization domain 153 164 192 UGN (= unbounded generating number) 6 63 Ultraproduct theorem 286 Unbound 228 Unbounded generating number (UGN) 6 63 Unbounded, totally 316 Uncleft, totally 189 Unfactorable matrix 269 Unique factorization domain (UFD) 153 164 192 Unique remainder algorithm 90 532 539 Unitriangular matrix 74 Universal denominators, theorem on 434 Universal field of fractions, R-field 281 389 Universal group of a monoid 35 Universal localization 390 Universal mapping property of free algebras 59 Universal object 548 Universal T-inverting monoid, ring 34 36 Upper multiplicative set 382 Valuation (ring) 302 452 531 Value 445 Vandermonde's identity 360 Weak 98 128 Weak algebra basis 104 129 Weak algorithm (n-term) 96 273 Weak algorithm (n-term) in a graded ring 101f. Weak algorithm (n-term), inverse 125 Weak algorithm, transfinite 139 Weak global dimension 256ff. 553 Weakly finite ring 6 63 Weakly semihereditary 13 Weight 342f. Weyl algebra, 55 265 Whitehead group 449 Whitehead lemma 451 453 Width of a graph 351 Wild automorphism 342 X-inner, X-outer automorphism 372 Zero (left, right) of a polynomial 514 Zero delay code 324 Zero object 545
Реклама
 |
|
О проекте
|
|
О проекте



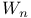

 -simple
-simple ,
, 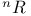
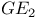
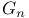 -ring
-ring 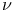 -basis of a right ideal
-basis of a right ideal