|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Gabriel P., Roiter A.V., Kostrikin A.I. (ed.) — Encyclopaedia of Mathematical Sciences. Volume 73: algebra VIII |
|
|
 |
| Предметный указатель |
![$(\Box+\circ,[1\ 1])$](/math_tex/9b576637211d4ba93e41949e87337f7a82.gif) 46 46
![$(\Box,[1])$](/math_tex/edcaf1d7c2aa1461039bea9479b4483b82.gif) 46 46
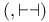 46 46
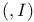 46 46
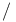 157 157
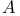 57 57
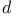 103 103
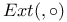 18 18
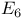 , , 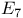 , , 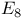 57 57
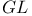 4 4
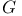 , , 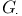 , , 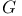 8 65 8 65
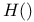 147 147
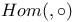 16 16
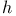 17 17
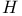 141 141
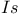 23 23
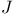 10 10
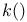 144 144
![$k[\Box]$](/math_tex/4cf8b1092950465151c1496e2ecaf21a82.gif) 74 74
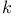 16 17 16 17
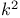 81 81
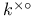 4 4
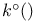 148 148
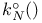 152 152
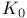 134 134
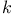 31 31
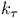 105 105
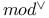 85 85
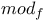 25 25
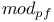 29 29
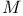 34 34
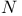 44 44
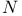 121 121
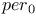 123 123
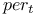 123 124 123 124
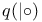 , , 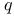 , , 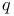 56 56
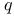 57 57
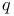 52 62 52 62
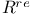 , , 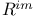 66 67 66 67
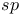 29 29
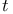 17 17
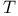 121 121
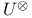 125 125
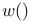 45 45
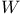 60 66 60 66
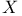 65 65
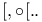 101 101
![$[\Box32,\circ]$](/math_tex/1d2c6b760e954dbb1432b94d291df1e382.gif) 32 32
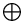 18 18
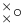 47 47
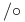 16 16
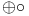 21 21
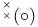 47 47
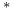 21 43 21 43
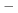 , , 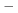 31 31
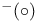 , , 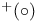 47 47
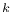 34 34
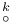 35 35
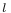 8 8
 , ,  159 159
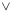 31 31
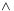 19 19
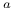 17 17
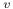 17 17
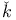 31 31
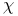 17 17
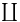 33 33
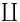 19 19
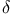 58 67 58 67
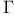 101 122—124 101 122—124
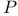 17 17
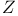 133 133
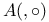 16 16
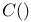 , , 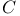 42 42
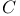 130 130
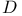 131 131
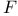 154 154
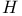 130 130
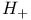 , , 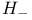 131 131
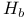 131 131
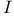 24 24
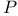 144 144
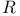 , , 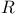 26 26
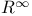 74 74
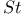 , , 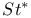 54 54
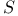 107 107
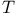 82 82
 16 16
 7 18 7 18
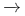 143 143
 107 107
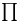 19 19
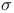 60 105 60 105
 , , 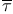 94 102 94 102
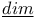 see "Dimension-function" see "Dimension-function"
 89 89
 127 127
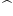 36 48 36 48
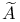 58 58
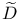 58 58
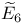 , , 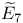 , , 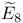 58 58
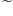 157 157
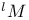 , , 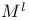 , , 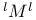 4 4
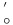 47 47
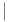 17 17
Abelian category 88
Additive category 21
Additive function 103
Additive hull 22
Admissible ideal 81
Affect 42
Aggregate 29
Algebra of a k-category, of a quiver 19
Almost split sequence 91
Annihilator of a module 45
Antichain 15
Arboresque 108
arrow 17
Artinian algebra 33
Avoid (space avoiding submodules) 34
Basis (of a module over a category) 43
Bigraph 56
Biinvolutive poset 43
Bimodule 15 88
c, C, 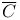 127 131 127 131
Canonical class 147
Category (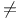 k-category) of paths 17 k-category) of paths 17
Chain (poset) 15
Cleaving 146
Closed under extensions ... 100
Closed under extensions path 102
Coherent (module, spectroid) 85
Cohomology group of a ray-category 147
Complete component 104
Conflation 89
contour 145
Convex subcategory 159
Cotranslate 91
Cover, covering 157
Critical arboresque spectroid 108
Critical form 57
Critical path 149
Critical ray-category 162
Cross-section 8
Cyclic 45
D 31
Deflation 87
Derivative (exact category) 131
Derivative (poset) 47
Derivatively equivalent 134
| Detect isomorphisms... 24
diamond 152
DIM see "Dimension"
Dimension of a module 29
Dimension-function 34 63
Dimension-vector 7
Direct sum of categories 33
Direct sum of modules 24
Direct sum of posets 55
Directed quiver 102
Display-functor 74
Distributive spectroid 142
Dualizing (spectroid, aggregate) 94
Dumb-bell 151
Dynkin graph 57
Eigenline 124
Elementary (representation) 46
Elementary (transformation) 4
Epivalence of categories 18
Equivalence of categories 24
Equivalence of representations of posets 7
Exact category, structure 87
Extended Dynkin 57 120
Extension 24 89
Faithful (module) 44
Final subset of a poset 101
Finite corepresentation 85
Finite k-category 29
Finite presentation 22
Finitely (module) 34
Finitely (poset) 46
Finitely (ray-category) 146
Finitely free 21
Finitely generated 84
Finitely injective 111
Finitely presented 22
Finitely projective 22
Finitely represented (k-category) 142
Finitely spaced 34 35
Full subcategory 24
Full subposet 55
Fully faithful functor 24
Fundamental cone 66
Fundamental group 157
Galois covering 159
Generation indicator 84
gldim  141 141
Grothendieck group 141
Head of an arrow 17
Hereditary 79 141
Ideal of a k-category 16
Idempotent 17
Identical path 17
Imaginary root 67
Immersion 21
ind  101 101
Indecomposable 24
Indicator of relations 84
Induction 83
Inflation 87
Injective (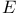 -injective) 89 -injective) 89
Injective envelope, envelopment 87
Injective-free 126
Interlaced 145
interval 31
Involutive representation 44
Isoclass 24
Isotropic generator 58
Isotropy group 65
k-category 16
k-category of paths 17
K-functor 16
Kernel of a k-functor 16
Linear matrix problem 8
Linearization (category) 16
Linearization (ray-category) 144
Local ring 32
Locally bounded 81
Locally finite quiver 81
Locular k-cateogry 25
Loop 17
Mapping cone 140
Matrix problem 8
Maximal dimension 34
Mesh - (sum, cateogry) 105
Minimal projective presentation 84
Minimal representation-infinite 149 155
mod  22 22
Modular equivalence 23
Module (over a category) 18 19
Module of relations 84
Module represented by an object 19
Multilocular k-category 25
Multiplicative basis 43
Normal (monomorphism) 100
Null object 21
Omnipresent representation 55 63
Omnipresent root 58
One-sided matrix problem 8
Oriented tree 118
Origin of a path 17
Parallel paths 17
Path of length d 17
Pattern 107
pdim  132 132
Penny-farthing 152
Piecewise hereditary 137
Pointwise finite 29
POSET 15
Positive form 56
Postprojective 104
Preinjective 104
Present (at a point) 39 46
Primitive idempotent 28
prin  88 88
Prinjective module 88
pro  22 22
Projection 21
Projection-functor 16
Projective (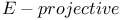 ) 90 ) 90
Projective cover, covering 87
Projective dimension 101
Projective-free 126
Proper submodule 32
Pull-up, push-down 159
Quasi-inverse functor 24
Quasi-surjective functor 16
quiver 17
Quiver of a k-category 73 74
Radical 26
Ray, ray-category 143
Real root 60 66
Reflection 60
rep  22 22
Repetition 81
Representation of a module 34
Representation of a poset 7
Representation of a quiver 20
Representation-quiver 101
Residue-category 16
Restriction of a unit form 56
Retraction 33
Root 52
S 130
S-category, S-functor, S-equivalence 141
S-sequence 140
Schurian 8
Section 33
Segment 8
Selfinjective 82
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



![$(\Box+\circ,[1\ 1])$](/math_tex/9b576637211d4ba93e41949e87337f7a82.gif)
![$(\Box,[1])$](/math_tex/edcaf1d7c2aa1461039bea9479b4483b82.gif)
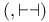
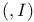
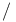
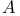
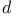
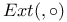
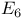 ,
, 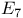 ,
, 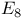
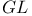
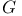 ,
, 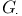 ,
, 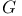
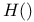
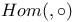
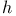
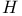
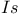
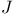
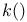
![$k[\Box]$](/math_tex/4cf8b1092950465151c1496e2ecaf21a82.gif)
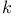
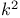
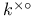
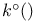
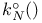
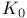
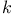
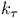
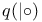 ,
, 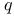 ,
, 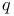
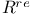 ,
, 
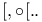
![$[\Box32,\circ]$](/math_tex/1d2c6b760e954dbb1432b94d291df1e382.gif)
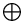
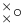
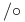
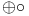
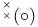
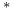
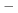 ,
, 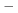
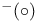 ,
, 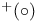
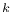
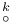
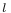
 ,
, 
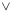
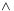
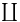
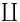
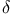
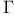
 ,
, 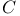
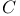
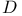
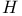
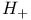 ,
, 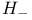
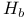
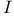
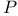
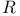 ,
, 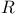
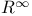
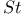 ,
, 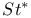
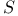
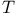


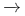

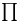
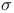
 ,
, 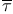
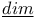


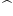
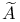
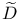
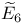 ,
, 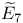 ,
, 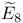
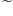
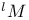 ,
, 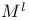 ,
, 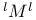
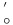
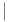
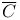
 k-category) of paths
k-category) of paths
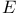 -injective)
-injective) 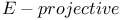 )
)