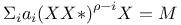|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Rao C.R., Mitra S.K. — Generalized inverse of matrices and its applications |
|
|
 |
| Предметный указатель |
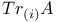 8 81 8 81
Adjoint matrix 4
Admittance matrix 181
Admittance-impedance conversion 185
Anderson, W.N., Jr. 188 189
Basis of a vector space 2
Basis of a vector space, dual basis 2
Basis of a vector space, reciprocal basis 2
Ben — Israel, A. 119 192 194 211
Best approximate solution 61 68
Best linear minimum bias estimator (BLMBE) 139
Best linear unbiased estimator (BLUE) 139
Bhimasankaram, P. 42 132
Bidiagonalization 5
BjBrck, A. 211
Bjerhammer, A. 16
Blattner, J.W. 69
Bleick, W.E. 153
Bott, R. 17 99
Businger, P. 211
Cayley — Hamilton theorem 8
Characteristic equation 8
Characteristic function (polynomial) 7
Characteristic function (polynomial), computation of 81
Charnes, A. 192 194 195
Chernoff, H. 203
Chipman, J.S. 138
Chisquare distribution, central 168
Chisquare distribution, noncentral 168
Cline, R.E. 16 67 71 98
Cochran's Theorem, generalization of 174
Cochran, W.G. 178
Cogredient transformation 121
Commuting hermitian matrices, transformation of 124
Commuting inverse 17 79
Commuting inverse, quasi commuting 93
Companion matrix 9 84
Computation of g-inverse 42 88 207
Conjugate transpose 12
Constrained inverse 17 98
Contragredient transformation 121
Convex programming 195
Craig — Sakamoto theorem 170
Craig, A.T. 170 178
Cyclic decomposition of a vector space 82
Cyclic spaces (types I and II) 83
Decell, H.P., Jr. 69
Decomposition theorem for matrices 33 93
Direct sum, matrices 10
Direct sum, vector spaces 3
Discriminant function 203
Disjoint (virtually) subspaccs 3
Drazin, M.P. 17 95
Duality theorem 50
Duffin, R.J. 17 99 188 189
Eigen values and vectors 8 86
Eigen values and vectors, 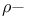 and and  -invers 74 -invers 74
Eigen values and vectors, generalized eigen value equation 43
Eigen values and vectors, generalized eigen vector 74
Eigen values and vectors, generalized null vector 89
Eigen values and vectors, inverse commuting with a power of the matrix 92
Eigen values and vectors, inverse with eigen value property 74 82 103
Eigen values and vectors, inverse with power property 78
Eigen values and vectors, of maximal height 89
Eigen values and vectors, parallel sum 191
Eigen values and vectors, proper eigen values 125
Eigen values and vectors, square partial isometry 116
Elementary divisors of a pencil 1 29
Englefield, M.J. 17 77
Equivalence of matrices 8
Erdelyi, I. 16 18 92 114
Faddeev, D.K. 81
Fisher — Cochran theorem 174
Frame, J.S. 16 28
Francis, J. 211
Frobenius inequality 18
g-Inverse, classification of,  -inverse 15 16 73 -inverse 15 16 73
g-Inverse, classification of, 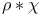 -inverse 16 97 -inverse 16 97
g-Inverse, classification of,  -inverse 15 16 75 -inverse 15 16 75
g-Inverse, classification of, 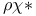 -inverse 16 97 -inverse 16 97
g-Inverse, classification of, 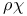 -inverse 15 16 75 76 79 80 -inverse 15 16 75 76 79 80
g-Inverse, classification of, basic solution 14 17 29
g-Inverse, classification of, commuting inverse 17 79
g-Inverse, classification of, commuting pseudoinverse 17 95
g-Inverse, classification of, constrained inverse 17 98
g-Inverse, classification of, general reciprocal 16
g-Inverse, classification of, group inverse 16
g-Inverse, classification of, least squares 14 16 48
g-Inverse, classification of, least squares, M-least squares 16 49
g-Inverse, classification of, left inverse 14 16 19
g-Inverse, classification of, left power inverse 16 98
g-Inverse, classification of, maximum rank 14 17 33
g-Inverse, classification of, minimum N-norm 14 45
g-Inverse, classification of, minimum norm 14 16 44
g-Inverse, classification of, minimum norm least squares 14 16 50
g-Inverse, classification of, Moore Penrose 16
g-Inverse, classification of, normalized generalized 16
g-Inverse, classification of, oblique 105
g-Inverse, classification of, pseudoinverse 16
g-Inverse, classification of, quasi-commuting 93
g-Inverse, classification of, reciprocal inverse 16
g-Inverse, classification of, reflexive inverse 14 16 27 68
g-Inverse, classification of, restricted 104
g-Inverse, classification of, right inverse 14 16 19
g-Inverse, classification of, right power inverse 16 98
g-Inverse, classification of, semi-inverse 16
g-Inverse, classification of, specified rank 31
g-Inverse, computation of 42 88 207
g-Inverse, definition 20 21
g-Inverse, expressions for different types 207
g-Inverse, representation of 26
g-Inverse, with specified properties, eigen value property 17 74 82 103
g-Inverse, with specified properties, from Jordan decomposition 17 87
g-Inverse, with specified properties, in the subalgebra of the matrix 80
g-Inverse, with specified properties, power property 77
g-Inverse, with specified properties, specified manifolds 72
Gantmacher, F.R. 1 128
Gauss — Markov model 136
Gauss — Markov model, addition or removal of observation 150
Gauss — Markov model, minimum bias estimator 138
Gauss — Markov model, multivariate case 154
Gauss — Markov model, optimality of least squares estimator 155
Gauss — Markov model, simultaneous estimation 141
Gauss — Markov model, singular covariance matrix 148
Gauss — Markov model, tests of linear hypothesis 142
Gauss — Markov model, unbiased estimator 137
Gauss — Markov model, validity of SLE for deviations in design & dispersion matrix 16
Gauss — Markov model, validity of SLE for deviations in design matrix 162
Gauss — Markov model, validity of SLE for deviations in dispersion matrix 155
Generalized eigen vector see “Eigen values and vectors”
Goldman, A.J. 16
Golub, G. 211 216
Graybill, F.A. 178
Greville, T.N.E. 68 69
Hadamard product 11
Henderson, C.R. 197
Hermite canonical form 4 18 33 40 209
Hogg, R.V. 178
Householder transformation 5 215
Householder, A.S. 1
Hypercompanion matrix 10
Idempotent matrix 13 23 31 111 118 119
Idempotents of a g-inverse 29
Ijiri, Y. 70
Impedance coefficients 184
Indefinite admittance matrix 181
Index (Drazin) of a matrix 91 96 97
Invariant factors 9
Jordan canonical form 10
Katz, I.J. 18
| Khatri — Rao product 12
Khatri, C.G. 12 41 70 111 178 204
Kirby, M. 195
Kronecker product 11 25 60
Kruskal, W. 157
Least squares inverse 14 16 48
Least squares, addition/removal of observation 150
Least squares, normal equations, solution of 213
Least squares, theory 140
Left inverse 14 16 19
Leverrier — Fadeev method 81
Linear programming, g-inverse for basic solution 29
Linear programming, interval 192
Linear programming, nonlinear convex programming 195
Marsaglia, G 178
Matrices of index 1 97
Matrices of index, equivalent conditions 18 71
Matrix equation 55
Matrix equation, best approximate solution of 61 68
Matrix types, EP 13 18
Matrix types, EPr 13 117 119
Matrix types, hermitian 13
Matrix types, idempotent 13 23 31 111 118 119
Matrix types, involution 118
Matrix types, nilpotent 13 93
Matrix types, nonnegative definite 13 41
Matrix types, normal 6 13 67 103 119
Matrix types, orthogonal 13
Matrix types, orthogonal complement 12
Matrix types, positive definite 13
Matrix types, positive semidefinite 13
Matrix types, semisimple 10 13 42
Matrix types, semiunitary 116
Matrix types, subunitary 114
Matrix types, symmteric 13
Matrix types, tripotent 113
Matrix types, unitary 6 13 114
Maximum Likelihood Estimation 201
Milne, R.D. 105
Minimal indices of a pencil 129
Minimum bias and variance estimation 139
Minimum bias estimator 138
Minimum norm (semi-norm) inverse 14 16 44
Minimum norm least squares inverse 14 16 50
Minimum polynomial 8 9 80
Minimum variance estimator 139
Mitra, S.K. 16 200 203
Mitra, Sanjit, K. 184
Moore — Penrose inverse 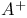 14 16 51 14 16 51
Moore — Penrose inverse 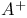 , expansion of 61 , expansion of 61
Moore — Penrose inverse 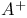 , expressions for 52 53 69 , expressions for 52 53 69
Moore — Penrose inverse 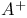 , incidence matrix 70 , incidence matrix 70
Moore — Penrose inverse 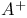 , Lagrange — Sylvester formula 61 , Lagrange — Sylvester formula 61
Moore — Penrose inverse 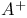 , Neumann type expansion 62 , Neumann type expansion 62
Moore — Penrose inverse 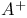 , partitioned matrix 71 , partitioned matrix 71
Moore — Penrose inverse 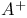 , product of matrices 67 , product of matrices 67
Moore, E.H. 16 50 101
Network theory, application of g-inverse, admittance impedance conversion 185
Network theory, impedance coefficients 184
Network theory, indefinite admittance matrix 181
Network theory, parallel sum of matrices (1) 186
Network theory, parallel sum of matrices (2) 188
Network theory, reduction of a multipole 183
Nilpotent matrix 13 35 93 104
Normal matrix 6 13 67 103
Null space 105
Oblique inverse 1C5
Odell, P.L. 17 76 89
Ogasawara, T. 172
Ogawa, J. 178
Orthogonal projector 108 111
Orthogonal subspace 3
Orthogonalization r.ieinod 210
Parallel sum of matrices 12 186 188
Partial isometry 3 114
Partial isometry, normal 119
Partial isometry, supplements of 116
Partitioned matrix, g-inverse of 41 64
Pearl, M.H. 18
Pease, M. C 1
Pedis, S. 1
Penrose, R. 16 51 68
Polar reduction of a matrix 7
Polar representatkn of a matrix 7
Power property, g-ir verse with 77
Principal idempoteits 35 104
Product of matrices, Hadamard 11
Product of matrices, Khatri — Rao 1 2
Product of matrices, Kronecker 11 25 60
Projection operator 3 106
Pyle, L.D. 210
Q-R algorithm 211
Quadratic forms, condition for independence 177
Quadratic forms, correlated case 171
Quadratic forms, distribution of 168
Quadratic forms, n.s. conditions for reducibility 121
Quadratic forms, pair of forms 120
Quadratic forms, reduction of 1 20
Quadratic forms, several forms 131
Quadratic forms, uncorrelated case 169
Rank factorization 5 21 28 209
Rao, C.R. 1 4 12 16 47 158 162 168 175 178 199 202 203 206 210 211
Reciprocal (dual) basis 2
Reduction of matrices, bidiagonalization 5
Reduction of matrices, diagonal 5 209
Reduction of matrices, hermite canonical form 4 18 33 40 209
Reduction of matrices, polar 7
Reduction of matrices, singular value 6 38 53 62 209 211
Reduction of matrices, spectral decomposition 5 38
Reduction of matrices, triangular 5 215
Reed, M.B. 186
Reflexive inverse 14 16 27 68
Reinsch.C 211 216
Right inverse 14 16 19
Robers, P.D. 194
Rohde, C.A. 16 41 103 197 201
Rosen, J.B. 17 30
Sakamoto, H. 170 178
Schur's lemma 12
Scroggs, J.E. 17 76 89
Searle, S.R. 197
Seminorm 3 46 49 51
Semisimple matrix 10 13 42
Semiunitary matrix 116
Seshu, S. 186
Shanbag, D.N. 172
Sharpe, G.E. 182 184
Sheffield, R.D. 16
Sibuya, M. 140
Similar matrices 9
Similarity invariants 9
Singular normal distribution 203
Singular value decomposition 6 38 53 62 209 211
Singular value decomposition, for two matrices 6
Singular value decomposition, MN decomposition 7
Singular values and vectors 12
Smith's canonical form 8
Solution of equations, ${(XX*)}^{-}X = M 60
Solution of equations, 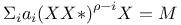 60 60
Solution of equations, A*XA = 0 25
Solution of equations, AX = 0 24
Solution of equations, AX = C, XB = D 25
Solution of equations, AX = Y 24 27
Solution of equations, AXB = C 24
Solution of equations, BXB = B, (BX)* = BX 57
Solution of equations, BXBXB = BXB 58
Solution of equations, XBX = 0 57
Solution of equations, XBX = 0, WBX = 0 57
Solution of equations, XBX = X 55
Solution of equations, XBX = X, (BX)* = BX 56
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



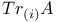
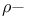 and
and  -invers
-invers 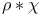 -inverse
-inverse  -inverse
-inverse 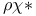 -inverse
-inverse  -inverse
-inverse