Авторизация
Поиск по указателям
Krause G.R., Lenagan T.H. — Growth of Algebras and Gelfand-Kirillov Dimension
Обсудите книгу на научном форуме Нашли опечатку?
Название: Growth of Algebras and Gelfand-Kirillov DimensionАвторы: Krause G.R., Lenagan T.H. Аннотация: During the two decades that preceded the publication of the first edition of this book, the Gelfand-Kirillov dimension had emerged as a very useful and powerful tool for investigating non-commutative algebras. At that time, the basic ideas and results were scattered throughout various journal articles. The first edition of this book provided a much-needed reliable and coherent single source of information. Since that time, the book has become the standard reference source for researchers. For this edition, the authors incorporated the original text with only minor modifications. Errors have been corrected, items have been rephrased, and more mathematical expressions have been displayed for the purpose of clarity. The newly added Chapter 12 provides broad overviews of the new developments that have surfaced in the last few years, with references to the literature for details. The bibliography has been updated and accordingly, almost double the size of the original one. The faithful revision and contemporary design of this work offers time-honored expertise with modern functionality: A keenly appealing combination. So, whether for the classroom, the well-tended mathematical books collection, or the research desk, this book holds unprecedented relevance.
Язык: Рубрика: Математика /Серия: Сделано в холле Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Издание: revised editionГод издания: 1999Количество страниц: 212Добавлена в каталог: 09.03.2011Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Algebra, almost commutative 61 73 Algebra, associated 182 Algebra, associated graded 64 Algebra, associated graded, noetherian 70 Algebra, Auslander — Gorenstein 187 Algebra, Auslander-regular 187 Algebra, catenary 112 188 Algebra, central simple 126 Algebra, Cohen — Macaulay 188 Algebra, commutative 39 Algebra, Filtered 64 Algebra, filtered, multi- 181 Algebra, finite dimensional 7 Algebra, finite dimensional, locally 14 Algebra, finitely generated 5 Algebra, free 7 Algebra, GK-partitive 190 Algebra, graded 61 Algebra, graded, connected 61 Algebra, graded, connected 180 Algebra, graded, finitely 61 Algebra, graded, homogeneous element of 61 Algebra, group 139 Algebra, Heisenberg 75 Algebra, Lie see “Lie algebra” Algebra, locally finite 180 Algebra, monomial 157 Algebra, normally separated 188 Algebra, PI see “Pi-algebra” Algebra, polynomial 9 Algebra, polynomial identity 125 191 Algebra, prime 48 Algebra, primitive 162 Algebra, quotient 39 Algebra, representable 191 Algebra, semi-commutative 179 Algebra, semiprime 49 Algebra, somewhat commutative 179 Algebra, strongly finitely presented 172 Algebra, strongly finitely presented, locally 172 Algebra, symmetric 67 Algebra, universal enveloping 7 109 Algebra, Weyl 26 87 183 Algebra, Weyl, quotient division algebra of 100 Annihilator 33 Bass’s formula 151 Bergman’s Gap Theorem 18 155 Bernstein class 89 Bernstein number 78 Bernstein’s inequality 88 189 Bimodule 54 Catenarity see “Algebra catenary” Center 39 cl. Kdim see “Krull dimension classical” Common denominator property 38 Commutator subgroup 140 Derivation 24 Derivation, 164 Derivation, locally nilpotent 42 169 Derivation, locally triangulizable 41 169 Differential operator 87 Dimension of level q 154 Dimension, bandwidth 155 Dimension, faithful 191 Dimension, filter 189 Dimension, Gelfand — Kirillov 14 51 Dimension, ideal invariant 56 Dimension, Krull, classical 40 Dimension, Krull, Gabriel — Rentschler 33 Dimension, q- 154 Dimension, super 13 154 Dimension, symmetric 56 Dimension, uniform 33 distribution 95 Dixmier map 112 187 Eigenvalue 41 Endomorphism, locally algebraic 164 Endomorphism, locally nilpotent 41 Endomorphism, locally triangulizable 41 Equivalent filtrations see “Filtration of module” Essential see “Module essential Exact see “Gelfand — Kirillov dimension” f-generating set see “Group nilpotent” f-growth see “Group nilpotent” f-length see “Group nilpotent” Faithful dimension see “Dimension faithful” Filter dimension see “Dimension filter” Filtration of algebra 64 Filtration of algebra, discrete 64 Filtration of algebra, finite 64 Filtration of algebra, multi- 181 Filtration of module 64 Filtration of module, discrete 64 Filtration of module, equivalent 68 Filtration of module, finite 64 Filtration of module, multi- 182 Filtration of module, standard 67 Finite uniform dimension 33 Free semigroup 15 Free semigroup, order ideal in 18 Free semigroup, word in 15 Free semigroup, word in, minimal period of 16 Free semigroup, word in, periodic 16 Function, analytic 95 Function, growth of see “Growth of function” Function, meromorphic 95 Function, periodically polynomial 175 Function, rational 174 Function, return 189 Function, test 95 g-stable ideal 110 Gelfand — Kirillov Conjecture 2 Gelfand — Kirillov dimension 1 Gelfand — Kirillov dimension of algebra 14 Gelfand — Kirillov dimension of algebra, lower 166 Gelfand — Kirillov dimension of algebra, upper 166 Gelfand — Kirillov dimension of bimodule 55 Gelfand — Kirillov dimension of module 51 Gelfand — Kirillov dimension of module, exact 53 69 73 131 136 172 191 Generating subspace of algebra 5 Generating subspace of module 51 GKdim see “Gelfand — Kirillov dimension” Goldie conditions see “Ring Goldie” Goldie’s Theorem 33 48 Grade see “Module grade Grading of algebra 61 Grading of module 62 Graph 156 Graph, adjacency matrix of 156 Graph, chain 156 Graph, cycle 156 Graph, growth 156 Graph, overlap 158 Graph, overlap, faithful 159 Graph, path 156 Graph, path, cyclic 156 Graph, path, length of 156 Graph, Poincare series of 156 Graph, Ufnarovskii 157 Gromov’s Theorem 139 196 Group, algebra 139 Group, finitely generated 139 Group, fundamental 140 Group, growth see “Growth of group” Group, linear 151 Group, nilpotent 139 Group, nilpotent, f-generating set 147 Group, nilpotent, f-growth 147 Group, nilpotent, f-length 147 Group, nilpotent, length of filtration 147 Group, nilpotent-by-finite 145 Group, polycyclic 142 Group, polycyclic, Hirsch number of 143 Group, solvable 139 Growth 1 Growth of algebra 6 Growth of function 6 Growth of group 140 Growth of group, exponential 140 Growth of group, intermediate 196 Growth of group, polynomial 140 Growth of group, subexponential 196 Growth of module 51 Growth, curve 155 Growth, exponential 6 Growth, intermediate 153 Growth, logarithmic 154 Growth, O(g(n))- 155 Growth, polynomial 6 Growth, subexponential 6 153 Height see “Prime ideal height Heisenberg group 145 197 Hilbert series 159 Hilbert — Samuel polynomial 68 76 78 Hodge algebra 19 Holonomic see “Module holonomic” Homogeneity see “Module homogeneous” Jacobson radical 126 Jacobson radical, nilpotent 126 Kaplansky’s Theorem 126 Kdim see “Krull dimension” Krull dimension, classical 40 Krull dimension, Gabriel — Rentschler 33 81 LD see “Transcendence degree lower” Ld-stable 186 Leading submodule 65 Lie algebra, 44 Lie algebra, algebraic 116 Lie algebra, enveloping algebra of 44 67 109 Lie algebra, finite dimensional 41 Lie algebra, infinite dimensional 7 Lie algebra, nilpotent 112 119 Lie algebra, semisimple 109 Lie algebra, solvable 44 84 109 localization 37 Localization at Ore sets arising from locally triangulizable inner derivations 169 Localization, central 127 167 Localization, normal 168 Markov’s theorem 195 Module, associated 182 Module, associated graded 64 Module, associated graded, noetherian 70 Module, essential submodule of 33 Module, filtered 64 Module, filtered, multi- 182 Module, grade of 187 Module, graded 62 Module, graded, 180 182 Module, graded, finitely 62 Module, graded, homogeneous element of 62 Module, holonomic 89 183 191 Module, homogeneous 60 113 Module, multiplicity of 178 Module, Noetherian 65 Module, pure with respect to grade 187 Module, smooth 59 Module, uniform 33 Multi-filtration 181 Multi-filtration, finite 182 Multiplicity see “Bernstein number” Nilpotent, group see “Group nilpotent” Nilpotent, ideal 57 172 Nilpotent, Lie algebra see “Lie algebra nilpotent” Nilpotent, radical 57 173 Noether Normalization Theorem 40 Normal element 115 168 Normal element, local 168 Order, admissible 181 Order, good 181 Ore, condition 37 Ore, extension 24 164 Ore, set 37 Ore, set, of normal elements 168 Partitive see “Algebra GK-partitive” Periodically polynomial function 175 PI-algebra 18 125 PI-algebra, finitely generated 127 PI-algebra, noetherian 131 PI-algebra, prime 126 PI-algebra, simple 126 PI-degree 130 Poincare series of filtered algebra 174 Poincare series of graded algebra 174 Poincare series of graph 156 Poincare series of group 197 Poincare series of monomial algebra 159 Poincare series, multi-variable 180 Poincare series, nonrational 197 Poincare series, rational 156 174—176 181 183 Poincare — Birkhoff — Witt, extension 163 Poincare — Birkhoff — Witt, Theorem 67 Polynomial identity 125 Polynomial, central 126 Polynomial, Hilbert see “Hilbert — Samuel polynomial” Polynomial, Hilbert — Serre see “Hilbert — Samuel polynomial” Posner’s theorem 126 Prime ideal of enveloping algebra of solvable Lie algebra 110 Prime ideal, height of 34 109 Primitive ideal 109 Pure see “Module pure Quillen’s Lemma 88 Quotient ring see “Ring of fractions” Rank 137 Rank of abelian group 169 Rank, reduced 137 Rational function 174 Regular element 33 Regular element, E(x)- 169 Return function see “Function return” Ring of differential operators 87 Ring of fractions 38 Ring, catenary 112 Ring, Goldie 33 Ring, irreducible 134 Ring, Krull symmetric 116 Ring, Noetherian 33 Ring, polynomial 26 Ring, power series 26 Ring, primary 134 Ring, prime 35 Ring, right FBN 173 Ring, semiprime 48 Ring, skew polynomial 164 Ring, skew-Laurent polynomial 144 190 Ring, skew-Laurent power series 101 Sensitive multiplicity condition 165 Superdimension see “Dimension super” Tauvel’s height formula 109 Tdeg-stable 184 Tensor product 28 165 Transcendence degree of a field 40 Transcendence degree of PI-algebra 126 Transcendence degree, Gelfand — Kirillov 106 167 183 Transcendence degree, lower 185 Volume difference inequality 185 Width of multi-index 104
Реклама
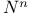-graded 
- 
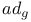-nilpotent subalgebra of 
|
|
О проекте