|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Giambruno A., Zaicev M. — Polynomial Identities and Asymptotic Methods |
|
|
 |
| Предметный указатель |
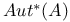 65 65
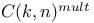 125 125
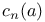 88 88
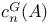 256 256
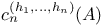 98 98
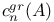 268 268
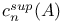 283 283
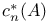 284 284
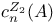 273 273
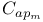 13 13
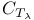 49 49
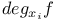 1 1
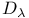 47 47
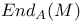 29 29
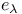 47 47
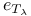 49 49
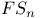 46 46
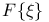 12 12
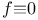 2 2
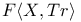 122 122
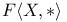 69 69
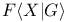 65 65
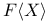 1 1
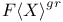 66 66
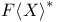 56 56
 69 69
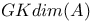 39 39
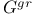 289 289
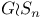 257 257
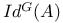 66 66
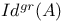 66 66
 284 284
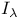 47 47
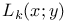 129 129
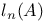 90 90
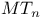 122 122
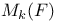 11 11
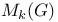 83 83
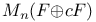 75 75
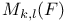 75 75
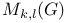 83 83
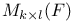 251 251
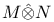 50 50
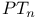 122 122
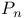 53 53
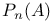 54 54
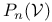 54 54
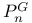 256 256
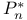 284 284
 268 268
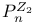 283 283
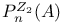 273 273
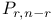 273 273
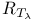 49 49
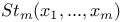 13 13
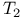 -ideal 80 -ideal 80
 47 47
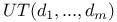 24 24
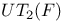 88 88
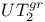 289 289
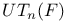 2 2
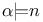 50 50
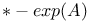 284 284
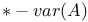 284 284
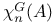 265 265
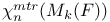 135 135
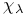 46 46
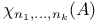 266 266
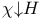 46 46
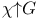 46 46
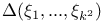 125 125
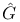 63 63
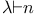 15 15
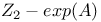 276 276
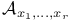 18 18
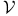 4 4
 82 82
 -ideals 73 -ideals 73
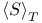 4 4
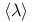 264 264
ADX 309
Algebra of generic elements 11
Algebra of generic matrices 12
Algebra of invariants 124
Algebra, algebraic of bounded degree 14
Algebra, center 31
Algebra, supercommutative 83
Algebra, verbally prime 83
Amitsur 35 36 104 106 108 215 242—245
Amitsur identity 109
Amitsur trick 100
Amitsur — Levitzki theorem 18
Antiautomorphism 65
Artinian ring 29
AT-algebra 317
Aut(A) 63
Berele 38 117 212 274
Birkhoff theorem 4
Block-triangular matrix algebra 24
Branching theorem 50
C(k,n) 125
Capelli identity 13
Capelli polynomial 13
Central localization 34
CHARACTER 45
Character, induced 46
Character, inner product 45
Character, irreducible 45
Cocharacter 54
Cocharacter, 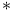 -cocharacter 284 -cocharacter 284
Cocharacter, G-cocharacter 265
Cocharacter, graded cocharacter 238
Cocharacter, mixed trace cocharacter 135
Cocharacter, pure trace cocharacter 123
Codimension 88
Codimension, 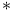 -codimension 264 284 -codimension 264 284
Codimension, 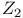 -codimension 273 284 -codimension 273 284
Codimension, G-codimension 256
Codimension, graded codimension 268 283
Codimension, supercodimension 283
Codimension, trace codimension 123
Colength 90
Column-stabilizer 49
Commuting ring 29
Decomposable monomial 259
deg f 1
Dense set 29
det(a) 2
Dilworth 94
Discriminant 125
Drensky 20 28 137 185 187 207
Element, skew-symmetric 69
Element, symmetric 69
Elementary symmetric function 15
Essential G-identity 262
Essential hook 241
exp(A) 144
exp(f) 215
EXPONENT 144
Exponent of a polynomial 215
Exponent, 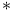 -exponent 284 -exponent 284
Exponent, 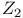 -exponent 276 -exponent 276
Exponent, superexponent 284
First Fundamental Theorem 125
Formanek 27 28 40 128 134 137
Free algebra with G-action 65
Free algebra with involution 69
Free algebra with trace 122
Free associative algebra 1
Free G-graded algebra 66
| Free Lie algebra 310
Free superalgebra 69
Free supercommutative algebra 83
Frobenius reciprocity 46
g-identity 66
Gelfand — Kirillov dimension 37
Generalized square 244
Generic division ring 40
Generic element 11
Generic matrix 12
Graded algebra 5 61
Graded algebra, 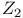 -graded algebra 65 -graded algebra 65
Graded algebra, G-graded algebra 61
Graded identity 66
Graded subalgebra 61
Graded subspace 61
Grassmann algebra 2 90
Grassmann envelope 81
GSPI-algebra 316
Gurevich 125
H(d,l) 58
h(d,l,t) 57
Halpin 28
Herstein 29
Homogeneous component 61
Homogeneous element 61
Hook 58
Hook formula 48
Hook number 48
Hook Theorem 105
Id(A) 3
Idempotent 45
Idempotent central 45
Idempotent essential 49
Idempotent minimal 45
Idempotent minimal graded 194
Indecomposable monomial 259
Induced module 46
Involution 69
Involution, exchange 77
Involution, symplectic 77
Involution, transpose 77
Jacobson 29
Kaplansky 27
Kaplansky's Theorem 31
Kasparian 28
Kemer 20 83 110 112 113 169
Koshlukov 20
Kostant 120
Krull dimension 39
Lattice permutation 51
Latyshev 94
Lewin Theorem 21
Lie algebra 307
Lie algebra, abelian 308
Lie algebra, adjoint representation 309
Lie algebra, center 309
Lie algebra, nilpotent 308
Lie algebra, representation 309
Lie algebra, simple 308
Lie algebra, solvable 308
Lie algebra, universal enveloping algebra 309
Lie commutator 2
Lie ideal 9
Lie identity 310
Littlewood — Richardson rule 51
Lower exponent 144
Maschke's Theorem 44
Mishchenko 184 268 289
Mixed trace polynomial 122
Monomial 1
Multilinearization process 7
Multipartition 264
Newton's formulas 15
Noether Normalization Theorem 39
Outer tensor product 50
Partition 46
Partition, conjugate 47
Permutation, d-bad 94
Permutation, d-good 94
PI-algebra 2
PI-exponent 144
Polynomial growth 171
Polynomial identity 2
Polynomial, alternating 12
Polynomial, central 26
Polynomial, consequence 7
Polynomial, equivalent 7
Polynomial, G-polynomial 66
Polynomial, homogeneous 5
Polynomial, linear 7
Polynomial, multialternating 138
Polynomial, multihomogeneous 5
Polynomial, multihomogeneous component 6
Polynomial, multilinear 7
Posner's theorem 34
Power sums symmetric function 15
Prime ring 34
Primitive ring 29
Procesi 27 40 123 125
Product of varieties 327
Pure trace polynomial 122
Razmyslov 19 20 27 28 123
Razmyslow — Kemer — Braun Theorem 35
Regev 94—96 108 117 128 141 184 212
Relatively free algebra 4
Representation 43
Representation, completely reducible 44
Representation, equivalent 44
Representation, irreducible 44
Representation, left regular 44
Robinson — Schensted correspondence 102
Rosset 18
Row insertion algorithm 101
Row-stabilizer 49
Rowen 33
s(A) 84
schur 120
Schur's lemma 29
Second Fundamental Theorem 125
Semiprime ring 32
Semistandard tableau 51
Sibirskii 125
Skew-tableau 51
Skolem — Noether theorem 78
SPI-algebra 314
Splitting field 30 45
Stable identity 10
Standard Lie polynomial 311
Standard polynomial 13
Standard tableau 47
Strip Theorem 107
Subdirect product 33
Superalgebra 65
Superalgebra, minimal 194
Superalgebra, reduced 240
Superenvelope 84
Supervariety 80
supexp(A) 284
Symmetric algebra 124
Symmetric function 15
Symmetric polynomial 15
T-ideal 3
T-ideal, verbally prime 82
tr deg(K/F) 39
tr(a) 2
Trace identity 122
Trace polynomial 122
Transcendence degree 39
Trivial grading 62
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



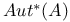
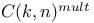
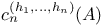
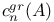
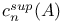
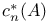
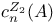
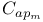
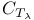
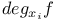
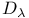
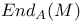
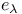
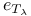
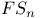
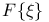
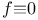
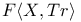
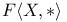
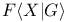
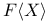
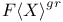
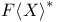

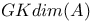
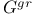
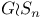
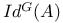
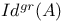

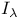
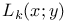
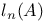
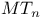
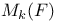
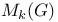
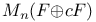
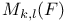
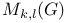
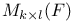
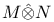
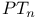
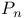
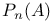
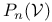
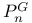
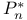

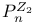
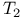 -ideal
-ideal 
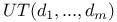
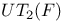
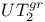
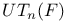
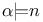
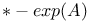
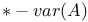
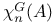
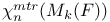
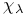
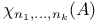
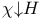
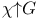
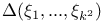
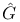
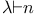
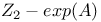
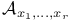
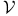

 -ideals
-ideals 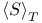
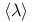
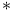 -cocharacter
-cocharacter 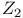 -codimension
-codimension