Авторизация
Поиск по указателям
Larsen R. — Banach algebras: An Introduction
Обсудите книгу на научном форуме Нашли опечатку?
Название: Banach algebras: An IntroductionАвтор: Larsen R. Аннотация: From author: "The exposition in the following pages is an elaboration and expansion of lectures I gave to second year mathematics graduate students at Wesleyan University during the academic years 1970-71 and 1971-72. The aim of the exposition is to provide a compact introduction to the theory of Banach algebras that not only acquaints the reader with fundamental portions of the abstract theory but also illustrates the usefulness of Banach algebras in the study of harmonic analysis and function algebras and gives the reader the basic tools necessary for further work in these areas. The first half of the book is devoted primarily to the general theory of Banach algebras, while in the second half the emphasis is on various more specialized topics related to harmonic analysis and function algebras - among which are: Wiener's Tauberian Theorem, the problem of spectral synthesis, the Bishop, Choquet, and 5ilov boundaries, representing measures, Werner's Maximality Theorem, the Commutative Gel'fand-Naimark Theorem, Plancherel's Theorem, the Pontryagin Duality Theorem, almost periodic functions, and the Bohr compactification.
Язык: Рубрика: Математика /Серия: Сделано в холле Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1973Количество страниц: 358Добавлена в каталог: 03.12.2010Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
114 17 102 228 4 29 29 156 158 316 317 97 17 92 92 228 16 16 88 167 88 227 11 182 182 197 228 173 117 184 114 126 214 215 198 186 107 110 188 199 114 19 18 93 93 12 293 309—310 46 280 18 104 46 123 71 139 273 6 16 14 17 21 116 18 282 3 3 20 162 71 168 115—116 225 221 54 66 69—70 86 70 69 78 74 287 113 74 121 128 105 22 20 22 18 134 20 A(d) 17 A(D), Bishop boundary for 228 A(D), Gelfand representation of, is not regular 167—168 A(D), maximal ideal space of 97 A(D), Silov boundary for 228 A(K) 17 A(X) 150 Adjoining an identity 10 Algebra 3 Algebra of absolutely convergent Fourier series 22 Algebra, Banach 4 Algebra, commutative 3 Algebra, division 35 Algebra, normed 4 Algebra, radical 82 Algebra, separating function 220 Algebra, uniform 255 Almost periodic compactification 329 Almost periodic function 18 323 AP (G) 18 Applications of boundaries 243—249 Approximate identity 109 Approximate identity in 109 188 Arens 1 Arens — Royden theorem 158 Arens, Theorem 48 A[e] 9 B*-algebra 273 B*-algebra, examples of 273—275 282 323 Banach algebra 4 Banach algebra at infinity 201 Banach algebra with involution 273 Banach algebra, belong locally to I, at a point 201 Banach algebra, commutative semisimple 81 Banach algebra, conditions to have an identity 153—154 178 Banach algebra, finitely generated 98 Banach algebra, maximal ideal discrete topological group 106 Banach algebra, normal commutative 176 Banach algebra, regular commutative 166 Banach algebra, self-adjoint commutative 132 102 Banach algebra, Tauberian commutative 183 Bdy(E) 51 Beurling — Gel’fand Theorem 81 Bishop boundary for a commutative Banach algebra 226 Bishop boundary for a separating function algebra 221 Bishop boundary for A(D) 228 Bishop boundary for C(X), X compact metric 227—228 Bishop boundary, example of nonexistence of 230—232 Bishop boundary, existence for a uniform algebra 268 Bishop-deLeeuw Theorem 236—237 Bohr compactification 329 Bohr compactification, uniqueness of 328 Boundary, applications of 243—249 Boundary, applications of Bishop 221 Boundary, applications of Choquet 242 Boundary, applications of existence of 222 Boundary, applications of Silov 225 Boundary, applications of, existence of 242 Boundary, applications of, for a commutative Banach algebra 226 Boundary, applications of, for a separating function algebra 221 C(V) 23 C(X) 16 C(X) is regular 167 C(X), Bishop boundary when X is compact metric 227—228 C(X), Choquet boundary for 242 C(X), closed ideals in 195 C(X), example of 230—232 C(X), Gel’fand representation of 87—88 C(X), maximal ideal space of 86 90 C(X), sets of spectral synthesis for 196 C(X), Silov boundary for 227 C*-algebra 275 CHARACTER 331 Character, continuous 113 Characterization of singular elements in C(X) 43 Characterization of singular elements in commutative Banach algebras 81 Characterization of singular elements in self-adjoint semisimple commutative Banach algebras 141 Choquet boundary, characterization of 257 263 Choquet boundary, characterization of existence of 242 Choquet boundary, characterization of, for A(D) 242 Choquet boundary, characterization of, for C(X) 242 Choquet boundary, characterization of, for separating function algebras 242 Choquet — Bishop-deLeeuw Theorem 271 Closed convex hull 233 Closed ideals in C(X) 195 Closed ideals in C(X) in 197 Closure operation 162 Commutative algebra 3 Commutative Gel’fand — Naimark Theorem 277 Compactification 323 Compactification, almost periodic 329 Compactification, Bohr 329 Compactification, Stone — Cech 90 Complex homomorphism 67 Connected component 1551 Connected component of the identity in 156 158 Continuity of inversion 31 Continuity of inversion of quasi-inversion 29 Continuous character 113 Contour, regular 143 Contour, spectral 144 Convex hull 233 Convex hull, closed 233 Convolution 19—20 Ditkin's condition 204 340 Division algebra 35 Dual group 127 EXP 156 Ext(E) 233 Extreme point 233 Finitely generated Banach algebra 98 Fourier coefficient 21 Fourier coefficient, homomorphism, complex 67 Fourier coefficient, transformation 21 115 277 Fourier — Stieltjes transform 128 Fourier — Stieltjes transform, homomorphism space 69 Function, almost periodic 18 323 Function, hull 160 Function, hull-kernel closure 162 Function, slowly oscillating 190 Functions which operate 151 Functions which operate, topology 163 Gel’fand representation 76 Gel’fand representation of 99 Gel’fand representation of 92 Gel’fand representation of 88 Gel’fand representation of 114 Gel’fand representation of 93 Gel’fand representation of a finitely generated commutative Banach algebra 99 Gel’fand representation of A(D) 97 Gel’fand representation of AC( 102 Gel’fand representation of C(X) 87—88 Gel’fand Representation Theorem 74 Gel’fand topology 71 Gel’fand transform 76 Gel’fand transformation 76 Gel’fand — Mazur theorem 35 H(I) 160 Haar measure 18 Ideal 4 Ideal, left 4 Ideal, maximal 4 Ideal, modular 7 Ideal, primary 216 Ideal, proper 4 Ideal, regular 7 Ideal, right 4 Ideal, two-sided 4 Identity modulo I 7 Int(K) 17 Inverse 5 Inverse, left 5 Inverse, right 5 Inversion theorem 298 301 Invertible 5 Involution 273 Isomorphism, topological 131 Joint spectrum 98 K(E) 160 Kernel 160 Kronecker approximation theorem 332 L(v) 22 Left ideal 4 Left ideal, inverse 5 Left ideal, modulus of integrity 46 Left ideal, quasi-inverse 13 Left ideal, topological zero divisor 40 Left ideal, zero divisor 40 Linear functional, multiplicative 67 Linear functional, positive 259 Local Maximum Modulus Theorem 220 M(G) 20 M(G) is semisimple 315 M(G), maximal ideal space of 128 Malliavinfs Theorem 199 Maximal ideal 4 Maximal ideal space 69 Maximal ideal space of 102 Maximal ideal space of 92 Maximal ideal space of 88 Maximal ideal space of 114 126 Maximal ideal space of 93 Maximal ideal space of 128 Maximal ideal space of a finitely generated commutative Banach algebra 99 Maximal ideal space of A(D) 97 Maximal ideal space of C(X) 86 90 Maximum modulus set 221 Maximum modulus theorem 218—219 Mergelyanfs Theorem 101 Modular ideal 7 342 Modulus of integrity 46 Modulus of integrity, left 46 Modulus of integrity, right 46 Multiplicative linear functional 67 Nilpotent 33 Nilpotent, topological 33 Noncommutative Gel’fand — Naimark Theorem 280 Normal commutative Banach algebra,quasi-invertible 13 176 Normed algebra 4 Plancherel transform 169 305 Plancherel transformation 169 305 Plancherelfs Theorem 169 301 307—308 Polynomial Spectral Mapping Theorem 57 Pontryagin duality theorem 312 Positive linear functional 259 Primary ideal 216 Proper ideal 4 Quasi-inverse 13 Quasi-inverse, left 13 Quasi-inverse, right 13 Quasi-regular 13 Quasi-singular 13 r(f) 55 R(K) 17 Rad(A) 82 Radical 82 Radical algebra 82
Реклама
 |
|
О проекте
|
|
О проекте





 , assumed after page
, assumed after page 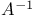
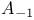
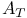

![$C^{n}([a,b])$](/math_tex/02205d9feafc903f20eb1a191dfad06f82.gif)
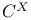

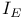
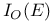
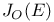
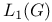 , closed ideals when G is compact
, closed ideals when G is compact 

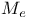


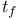

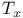
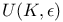
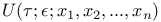
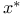
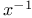








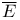
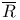
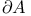

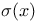

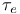
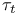
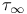

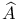
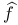
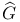
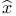

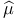
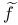

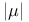


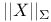
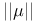

![$C^{n}([a, b])$](/math_tex/ff46e3c3284879bbd1f56647b85316fc82.gif)
 )
) 