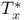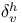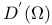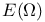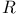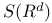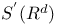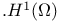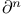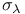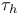|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Rauch J. — Partial differential equations |
|
|
 |
| Предметный указатель |
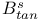 216 216
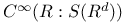 101 101
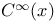 227 227
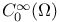 248 248
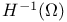 191 191
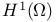 192 192
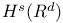 89 89
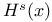 165 187 225 165 187 225
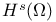 225 225
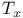 , , 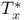 28 28
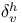 220 220
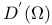 248 248
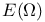 248 248
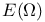 , metric for 254 , metric for 254
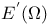 253 253
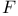 64 64
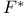 67 67
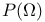 248 248
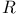 69 69
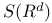 61 61
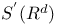 74 74
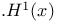 228 228
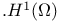 184 184
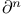 12 12
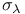 66 66
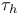 66 250 66 250
Acoustic waves 117 see
Airy equation 139ff 150
Burgers' equation 20ff 31 55ff 140
Cauchy — Kowaleskaya, theorem §1.3—§1.8 230
Cauchy — Riemann equations 4 15 81 §3.8 124 144
Characteristic(s) 30 40 §1.9 125 215
Characteristic(s), curves 3 19 21
Characteristic(s), lines 2 30
Characteristic(s), surfaces 30 31
Characteristic(s), variety 31 95
Coercive 189 193 195 225
Comparison theorem 141 243
Conormal 30 216
Conormal space 30
Conormal variety 30
Convolution §2.5 252 256
Cotangent space 29
Critical point 178 180
D 26
d'Alembert's formula 43ff §4.5
Descent, method of §4.8
Dilation 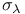 66 77 139 66 77 139
Dirac's delta function 249
Dirichlet problem 118 Ch.
Dirichlet's principle 178ff
Discontinous dependence 121 124 130 157
dispersion 103 105 107 149 150
Dissipation 120 215
distribution 248ff Ch.
Domain of determinacy 2 3 43ff 152 161
Domain of influence 2 3 43ff 152 161
Duhamel's principle §3.11 §4.9
Eigenfunction expansions 70 201 §5.7
Eikonal equation 30
Elliptic equations and operators 1 6 31 42 54 81 96 106 172 191 Ch.
Elliptic regularity theorem 80—81 201 226
Elliptic regularity theorem, boundary 229ff
Elliptic regularity theorem, interior 227ff 239
Elliptic regularity theorem, tangential §5.8
Ellipticity constant 189
Energy method 114 116 120 139 140 191
Euler equation 174 190 193
Fixed point equation 10 205
Fourier transform §2.2ff
Frechet space 63 123
Fredholm alternative, for elliptic boundary value problems §5.6 244
Fundamental solution 85 86 104 §4.2
Generalized Schwartz inequality 90 108 111
Generalized solution 104 §3.5 119 212
Greens function 85 86 §4.2
Group velocity 99 102 149 150
| Hadamard — Petrowsky condition §3.10 134 139 177
Harmonic function 17 81 157 175 176 238—239
Hausdorff — Young inequality 86
Heat equation 12 13 16 40 81 §3.6 §3.7 131 133 134 §4.2 §4.3 172ff 177ff 196 211ff 215
Heisenberg's uncertainty principle 97 98 99 105
Hodge theory 194ff 216 228
Holmgren's uniqueness theorem 16 §1.7 98 111 124
Holmgren's uniqueness theorem, global §1.8 99 126
Holmgren's uniqueness theorem, semiglobal 39
Holomorphic function 5 17 81 144 236
Huygen's principle 160 162 164 165
Huygen's principle, generalized 165
Hyperbolic equations 1 96 127 162 228
Initial value problem Ch. 1 Ch. Ch.
Laplace equation 12 15 81 131 157
Laplace — Beltrami operator 188 216
Lax duality theorem 90 111
Linearization 20 22 23 26 175
Loss of derivatives 131 156 157 161
Maximum principles Cor. 4.3.4 172 §5.10 §5.11
Mean curvature 174 176 246
Mean value property 176 236 238ff
Measure(s) 141 164
Measure(s), Fourier transform of 82
Method of characteristics 19 131
Minimal surface 174 246
Monotonicity 161 165
Natural boundary condition(s) 194 196
Neumann problem 188 191 193 206 224—225 244
Noncharacteristic 18 19 23 25 30 32 40 §1.8 124 127
Nonstationary phase 149 150 166
Null solutions 41 98 111 §3.9
Order, of a distribution 249
Orthogonal invariance 86 153 154
Orthogonal transformation 70
Paley — Wiener theorem 86 122
Parabolic equations 13 96 106 107 163 211ff
Peter — Paul inequality 182
phase velocity 99 102 150
Poisson kernel 176
Propagator 134 Ch.
Propagator, heat 113 §4.2 §4.3
Propagator, Schroedinger 103 §4.2 §4.3
Propagator, wave 118 §4.2 §4.5 §4.7 §4.8 §4.9
Push forward 216 220
Quasi-linear trick 116 246
Radiation problems §4.9
Rarefaction wave 56 140
Real analytic function 5 8 11 17 24 144
Reflection of waves 152
Reflection operator 69 70 84 251
Regular boundary point 228
Rellich compactness theorem 202
Riesz — Thorin convexity theorem 72 142
Robin problem/boundary condition 196 244
Schroedinger's equation §3.2 §3.3 §3.4 §3.5 126 131 134 §4.2 §4.4 212
Self-similar 58 60 139 140
Separation of variables 207 211—214
Shock waves 6 54 59
sing supp 165
Smoothing property 143 212 215
Sobolev embedding theorem 93 184 187 210 228 231
Sobolev spaces §2.6
Sound waves 21 57 117
Subharmonic function 179 235
Support 248 253
Symbol of a differential operator §1.6
Tangent space 28 30
Taylor's theorem 136
Tempered distributions §2.4ff
Tempered distributions, convergence 75
Trace, at boundary 196 198 200
Translation, 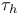 66 77 250 66 77 250
Transpose of a differential operator 34 252
Transpose of a linear operator 34 76 251
Wave equation, damped or with friction 120 180 212 214
Wave equation, wave operator 12 31 43ff §3.7 131 133 136 §4.2 §4.5 §4.6 §4.7 §4.8 §4.9 212
Weak well-posed 131 132
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



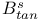
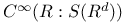
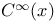
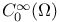
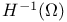
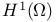
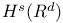
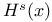
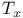 ,
,