|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Triebel H. — Theory of Function Spaces |
|
|
 |
| Предметный указатель |
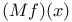 14 14
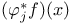 53 53
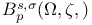 261 261
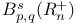 166 166
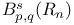 45 45
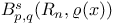 257 257
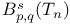 265 265
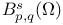 192 192
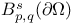 192 192
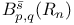 270 270
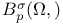 261 261
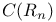 36 36
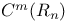 36 36
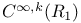 165 165
 -domain 191 -domain 191
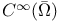 194 194
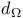 246 246
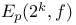 80 80
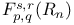 218 218
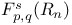 45 45
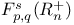 166 166
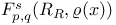 257 257
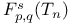 265 265
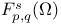 192 192
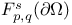 193 193
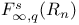 46 50 46 50
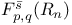 270 270
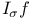 58 58
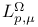 22 22
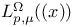 252 252
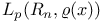 256 256
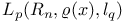 255 255
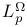 22 22
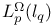 29 29
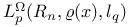 254 254
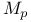 120 120
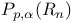 147 147
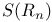 12 12
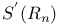 12 12
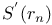 -analytic function 67 -analytic function 67
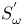 246 246
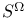 15 15
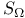 246 246
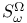 250 250
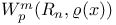 258 258
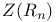 237 237
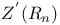 237 237
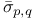 81 81
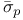 81 81
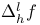 36 36
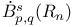 238 238
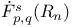 238 238
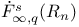 239 239
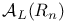 52 240 52 240
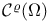 198 198
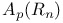 44 80 44 80
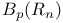 44 44
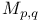 128 128
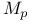 120 120
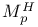 120 120
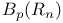 79 79
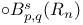 180 180
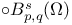 209 209
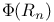 45 237 45 237
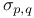 32 81 32 81
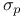 26 81 26 81
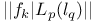 14 14
| 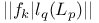 14 14
Besov space 34 37 51
Bessel-potential space 34 37 51
BMO 35
bmo(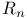 ) 37 51 ) 37 51
Complex interpolation 66
Convolution 28
Convolution algebra 28 127
Coretraction 132 167
Diffeomorphism 173
Embedding theorem 129
Embedding theorem, direct 131
Embedding theorem, inverse 132
Extension 166 190
Extension operator 167
Fourier multiplier 25 57 73 88 91 117 118 119
Fourier transform 13
Fubini property 114
Function space 33
Haar function 195
Hardy space 35 38 243
Hardy — Littlewood maximal function 14
Hoelder space 36 51
Homogeneous Fourier multiplier 118
Inequalities of Plancherel — Polya — Nikol'skij type 11
Interpolation method 62
Interpolation property 63
Interpolation, complex 203
Interpolation, real 203
Lebesgue space 34 37
Lifting property 58
Liouville space 34 37
Lipschitz space 34 37
Littlewood — Paley function 182
Littlewood — Paley theorem 93
Lizorkin representation 85
Local Hardy space 37 51 73
localization 190
Lusin function 182
Maximal function 53
Multiplication algebra 145
Multiplier 140 158
Multiplier, pointwise 140 197
Nikol'skij inequality 18
Paley — Wiener — Schwartz theorem 13 248
Plancherel — Polya — Nikol'skij type, inequalities of 11 properly elliptic 213
Quasi-Banach space 14
Quasi-norm 14
Real interpolation 66
Real interpolation space 63
Real method 62
Rectification 190
Resolution of unity 192
Retraction 132 167
Schauder basis 87
Schwartz space 12
Semi-group, Cauchy — Poisson 183
Semi-group, Gauss — Weierstrass 183
Slobodeckij space 34 36
Sobolev space 36
System, complemented 214
System, normal 213
System, regular elliptic 214
Trace 131 139
Ultra-distributions 245
Weak Fourier multiplier property 40
Zygmund space 34 36 51
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



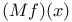
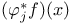
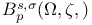
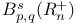
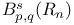
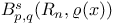
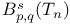
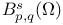
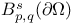
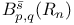
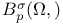
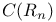
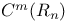
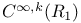
 -domain
-domain 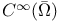
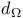
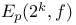
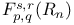
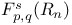
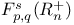
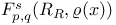
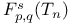
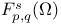
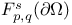
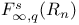
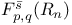
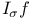
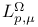
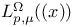
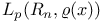
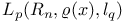
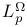
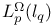
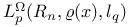
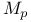
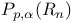
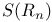
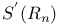
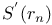 -analytic function
-analytic function 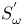
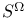
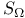
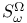
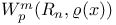
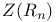
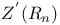
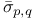
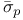
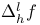
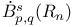
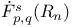
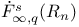
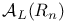
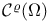
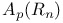
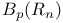
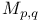
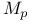
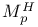
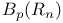
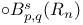
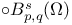
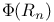
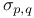
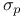
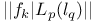
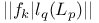
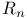 )
)