|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Stetter H. J. — Numerical polynomial algebra |
|
|
 |
| Предметный указатель |
Normal set representation, admissible data 295
Normal set representation, algorithmic computation 418
Normal set representation, approximate 355 357
Normal set representation, approximate, refinement 358 363
Normal set, border subset 282
Normal set, border web 291
Normal set, boundary set 290
Normal set, feasible 57
Normal set, generic 317
Normal set, quasi-univariate 282
Norms of linear maps 81
Numerical basis computation 429
Numerical basis computation, empirical data 433
Numerical basis computation, pivoting 432
Numerical basis computation, reduction to zero 430 431
Numerical data 101
Numerical instability 110
O(1) 69
Orthogonal polynomials 137
Pivoting 432
plex 314
Polynomial 4
Polynomial combination 14
Polynomial division 157
Polynomial division, algorithm 157
Polynomial division, backward error 160
Polynomial division, empirical polynomials 160
Polynomial interpolation 61
Polynomial interpolation, approximation error 166
Polynomial interpolation, backward error 169
Polynomial interpolation, empirical data 168 407
Polynomial interpolation, multivariate 404
Polynomial interpolation, sensitivity 166
Polynomial interpolation, smoothing 169 407
Polynomial interpolation, univariate 163
Polynomial system, BKK-deficient 400
Polynomial system, cluster about  403 403
Polynomial system, empirical 72
Polynomial system, in one variable 206
Polynomial system, multiple zero 328
Polynomial system, near-singular 387
Polynomial, empirical 71
Polynomial, homogeneous 4
Polynomial, sparse 5
Polynomial, support 4
Polynomial, total degree 4
Polynomial, zero set 15
Polynomials, order-leading term 315
Polynomials, orthogonal 137
Polynomials, spaces of 137
Polynomials, systems of 6
Polynomials, univariate 135
Positive-dimensional polynomial systems 447
Positive-dimensional polynomial systems, quotient ring with parameters 463
Positive-dimensional polynomial systems, quotient rings, normal sets 447
Positive-dimensional polynomial systems, zero sets from multiplication matrices 457 460
Problem, ill-conditioned 79
Problem, ill-posed 76
Problem, overdetermined, singular 77
Problem, well-posed 76
Product mapping 13
Pseudo-inverse 382
Pseudodivisor 184
Pseudofactors 255
Pseudomultiple 192
Pseudoresult sets 73
Pseudozero domains 152
Pseudozero domains, m-fold 202
Pseudozero domains, simultaneous 153
Quasi-univariate normal set 282
Quotient ring 31
Quotient ring, basis 29
Quotient ring, Lagrange basis 30
Quotient ring, multiplication matrices 34
Quotient ring, univariate 143
Rank 14
Reduced Groebner basis 320
Regular system 273 344
Regular system, Newton polytope 311
Regular system, number of zeros 309
Representation singularity 325
Residue class 29
Residue class ring 31
Result refinement 95
| Result space 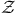 73 73
Resultant 248
Ring 12
Ring, commutative 12
Round-off error 118
S-polynomial 292
Separating linear form 301
Singular linear system 382
Singular matrix eigenproblem 452
Singular matrix eigenproblem, algorithmic solution 454
Singular matrix eigenproblem, regular eigenvalue 453
Singular matrix eigenproblem, solution space 453
Singular point 246
Singular point, manifold structure 251
Singular polynomial system 381
Singular polynomial system, with diverging zeros 398
Singular problem 77
Singular zero 246
Singular zero, determination 249
Singularity manifold 325
Smoothing interpolation 407
Specified value empirical data 68
Stable numerically 109
Staircase 321
Support 4
Support, empirical 71
Sylvester matrix 178 185
Sylvester matrix, rank deficiency 208
System of polynomials 6
System of polynomials, complete intersection 18
System of polynomials, d-dimensional 19
System of polynomials, multivariate 273
System of polynomials, positive-dimensional 447
System of polynomials, resultant 248
Syzygy 27
Syzygy, (non)trivial 27
Syzygy, nontrivial 294
Syzygy, of border basis 290
Syzygy, trivial 294
S[p,q] 292
Taylor expansion 8
Tdeg 314
Term order 60 314
Term order, lexicographic, graded, total degree 314
Tolerance empirical data 68
Univariate ideal, basis 140
Univariate ideal, normal set 140
Univariate polynomials 135
Univariate polynomials, backward error of zeros 149
Univariate polynomials, common divisor 206
Univariate polynomials, common zeros 206
Univariate polynomials, decomposition 140
Univariate polynomials, division 157
Univariate polynomials, expansion 140
Univariate polynomials, interpolation 163
Univariate polynomials, intrinsic 135
Univariate polynomials, Lagrange basis 142
Univariate polynomials, multiple zeros 202
Univariate polynomials, normal form 140
Univariate polynomials, pseudozero domains 152
Univariate polynomials, real zeros 178
Univariate polynomials, stable 180
Univariate polynomials, zero cluster 195
Univariate polynomials, zeros 146
Univariate polynomials, zeros with large modulus 154
Unstable numerically 109
Valid instance 68
Valid result 74
Validity scale 69
Vandermonde matrix 142
Visualization 19
V[..] 17
Well-conditioned problem 79
Zero cluster 194 366
Zero cluster, asymptotic behavior 377
Zero cluster, dual space 367
Zero cluster, valid 367
Zeros, clustered about oo 204
Zeros, m-fold 43
Zeros, singular 246
Zeros, well-separated 152 198
Zeroset 15
Zeroset, continuity 305
Z[..] 15
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте