|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Pears A.R. — Dimension theory of general spaces |
|
|
 |
| Предметный указатель |
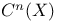 92 92
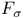 -set 19 -set 19
 -set 19 -set 19
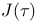 , the metrizable hedgehog 86 , the metrizable hedgehog 86
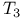 -space 9 -space 9
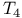 -space 17 -space 17
 -closed set 49 -closed set 49
 -discrete family 11 -discrete family 11
 -locally finite family 11 -locally finite family 11
Accumulation point 4
Algebra 69
Algebra, complete normed 371
Algebra, normed 371
Almost-open mapping 207
Analytic base 390
Analytic dimension ad 390
Analytic subalgebra 387
Analytic subalgebra L[H] 388
Baire space 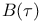 84 84
Baire’s theorem 93
Bank of a family of sets 145
Base for a topology 3
Bicompact space 37
Bicompactification 42
Bicompactification, Stone — Cech 46
Bing’s theorem 80
Boundary 12
Brouwer theorem 10
C(X) 92
Canonical covering 214
Canonical mapping into a nerve 108
Canonical mapping of an inverse system 52
Cantor manifold 362
Cantor set 150
Cantor space, n-dimensional 335
Cauchy sequence 91
Chain 2
Closed covering 4
Closed mapping 6
Closed set 3
Closed subalgebra A[H] 371
Closed unit ball 10
Closure 3
Cofinal subset of a directed set 52
Compact space 35
Complete normed algebra 371
Complete space 91
Completely normal space 27
Completely paracompact space 76
Completely regular space 39
Component 4
Connected space 3
Connecting mapping 52
Constancy set 376
Continuous function 5
Countable sum theorem for covering dimension 125
Countable sum theorem for large inductive dimension 171
Countably paracompact space 66
Covering 4
Covering dimension dim 111
Covering, canonical 214
Covering, closed 4
Covering, numerable 22
Covering, open 4
Covering, shrinkable 20
Cozero-set 18
Cushioned refinement 68
Cut 312
CW-complex 296
Decomposing mapping 398
Dense set 4
Diameter, diam 77
Dimension of a CW-complex 297
Dimension of a distributive lattice 366
Dimension of a mapping 336
Dimension of a simplicial complex 105
Dimension,  217 217
Dimension, 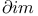 368 368
Dimension, analytic, ad 390
Dimension, approximation 238
Dimension, at a point 197
Dimension, cofinal approximation 238
Dimension, covering, dim 111
Dimension, large inductive, Ind 155
Dimension, local inductive, locInd 188
Dimension, local, locdim 188
Dimension, small inductive, ind 150
Dimensional rank dr 378
Dimensional weight dw 404
Directed family of coverings 215
Directed set 1
Discrete family 11
Discrete topology 3
Distributive lattice 2
Dominated space, by a covering 14
Embedding 7
Envelopment 391
Equivalent bicompactifications 43
Equivalent pseudo-metrics 77
Euclidean n-space  10 10
Examples, 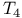 space M such that dim M = Ind M > 0 and ind M = 0 203 space M such that dim M = Ind M > 0 and ind M = 0 203
Examples, 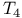 -space for which the subset theorem fails for local dimension 203 -space for which the subset theorem fails for local dimension 203
Examples, 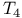 -space X such that -space X such that 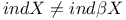 234 234
Examples, 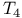 -space Z such that ind Z = 0, dim Z = 1 and Ind Z = 2 208 -space Z such that ind Z = 0, dim Z = 1 and Ind Z = 2 208
Examples, bicompact space for which the subset theorem does not hold for dim or Ind 161
Examples, bicompact space S such that dim S = 1 and ind S = Ind S = 2 165
Examples, bicompact space X such that ind X = 2 and Ind X = 3 329
Examples, completely normal 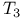 -space which is not totally normal 33 -space which is not totally normal 33
Examples, dimension of a subspace of R 152
Examples, dimension of the rational points in Hilbert space; a totally disconnected space of positive dimension 153
Examples, dimension of the unit interval 113
Examples, metrizable space P such that ind P = 0 and dim P = 1 288
Examples, metrizable space which is not strongly metrizable 86
Examples, strongly metrizable space which is not strongly paracompact 84
Examples, Tihonov space Y such that 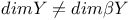 234 234
Examples, Tihonov space Y such that 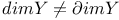 368 368
Examples, totally normal space which is not perfectly normal 73
Examples, zero-dimensional completely normal space with an open subspace of positive dimension 139
Examples, zero-dimensional normal space which is not weakly paracompact 130
Examples, zero-dimensional open mapping which lowers dimension 348
Examples, zero-dimensional spaces with product of positive dimension 354
Extension 19
F-product 357
Face of a simplex 105
Family of functions, separating points 40
Family of functions, separating points from closed sets 40
Filippov’s example 308ff
Fine family of coverings 216
Finite intersection property 35
First-countable space 82
Generalized 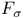 -set 28 -set 28
Geometric realization 106
Greatest lower bound 1
Hausdorff space 8
Hedgehog 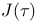 86 86
Hereditarily paracompact space 73
Hilbert cube 88
Hilbert space 88
Homeomorphism 6
Homeomorphism, local 190
Homomorphism of algebras 370
Homomorphism of normed algebras 371
Homotopic mappings 121
Homotopy 121
I, unit interval 5
Ideal of a distributive lattice 49
Ideal of an algebra 370
Identification mapping 8
Identification topology 7
Image of a homomorphism 370
| Ind, large inductive dimension 155
ind, small inductive dimension 150
Independent family of sets 144
Inessential mapping 127
Infimum 1
Interior 3
interval 2
Interval topology 4
Inverse limit 52
Inverse system 52
Irreducible mapping 218
Isometry 371
Kernel of a homomorphism 370
Kuratowski lemma 2
Large inductive dimension Ind 155
Lattice 2
Least upper bound 1
Light mapping 398
Lindeloef space 75
Linear order 2
Linearly ordered set 2
Linearly ordered space 5
Local dimension locdim 188
Local homeomorphism 190
Local inductive dimension locInd 188
Locally finite family 11
Long line 163
Lower bound 1
Mapping 5
Mapping, 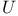 -, where -, where 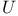 is an open covering 90 is an open covering 90
Mapping, almost-open 207
Mapping, canonical, into a nerve 108
Mapping, canonical, of an inverse system 52
Mapping, closed 6
Mapping, connecting 52
Mapping, continuous 5
Mapping, decomposing 398
Mapping, dimension-lowering 340
Mapping, dimension-raising 344
Mapping, identification 8
Mapping, inessential 127
Mapping, irreducible 218
Mapping, light 398
Mapping, open 6
Mapping, perfect 94
Mapping, special irreducible 311
Mapping, zero-dimensional w.r.t. an open covering 392
Maximal element of a partially ordered set 1
Maximal ideal of a distributive lattice 49
Maximal ideal of an algebra 370
Maximal ideal space 50
Mesh of a covering 253
Metric 9
Metric space 9
Metrizable space 10
Minimal element of a partially ordered set 1
Monotone scale of an N-space 288
Monotonicity of dimension 138ff 193ff
N, set of positive integers 3
n-Space 288
Nagata — Smirnov theorem 78
Neighbourhood 3
Nerve of a covering 108
Normal space 17
Normally situated set 28
Normed algebra 371
Numerable covering 22
Open ball 9
Open covering 4
Open mapping 6
Open refinement 4
Open set 3
Open-and-closed set 3
Order of a family of sets 111
Order-complete linearly ordered set 2
Paracompact M-space 101
Paracompact space 57
Partial order 1
Partially ordered set 1
Perfect mapping 94
Perfectly normal space 33
Perfectly zero-dimensional space 217
Point-finite family 11
Polyhedron 108
Precedence, partial order of bicompactifications 43
Pseudo-metric 9
Pseudo-metric space 9
Pseudo-metric topology 9
Pseudo-metrizable space 9
Quasi-order 1
Quasi-ordered set 1
Quotient space 8
R, set of real numbers 5
Rank rk of a subset of a normed algebra 390
refinement 4
Refinement, closed 4
Refinement, cushioned 68
Refinement, open 4
Refinement, star- 70
Refinement, strong star- 70
Refinement, weak 76
Regular family of coverings 216
Regular space 8
Replica of an N-space 290
retract 7
Retraction 7
Roy’s example 271ff
Separable space 86
Separation axioms 8
Separation of sets 119
Shrinkable covering 20
Similar families 24
simplex 105
Simplicial complex 105
Skeleton of a simplicial complex 106
Small inductive dimension ind 150
Space, 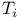 -space, i = 0,1,2 8 -space, i = 0,1,2 8
Space, Baire 84
Space, bicompact 37
Space, Cantor 335
Space, compact 35
Space, complete 91
Space, completely normal 27
Space, completely paracompact 76
Space, completely regular 39
Space, countably paracompact 66
Space, dominated by a covering 14
Space, Euclidean 10
Space, first-countable 82
Space, Hausdorff 8
Space, hereditarily paracompact 73
Space, Hilbert 88
Space, Lindeloef 75
Space, linearly ordered 5
Space, metric 9
Space, metrizable 10
Space, normal 17
Space, paracompact 57
Space, perfectly normal 33
Space, perfectly zero-dimensional 217
Space, pseudo-metrizable 9
Space, quotient 8
Space, regular 8
Space, separable 86
Space, strongly paracompact 74
Space, strongly pseudo-metrizable 83
Space, Tihonov 39
Space, topological 3
Space, totally disconnected 112
Space, totally normal 31
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



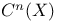
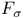 -set
-set  -set
-set 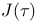 , the metrizable hedgehog
, the metrizable hedgehog 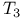 -space
-space 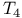 -space
-space  -closed set
-closed set  -discrete family
-discrete family 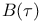

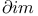

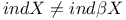
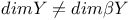
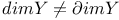
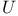 -, where
-, where 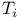 -space, i = 0,1,2
-space, i = 0,1,2