|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Patterson S.J. — An Introduction to the Theory of the Riemann Zeta-Function |
|
|
 |
| Предметный указатель |
Algebraic geometry 76 82—84
Apery, R. 3
Approximate functional equation 8 23 50 67 91ff
Artin L-functions 82
Artin, E. 75
Bernoulli numbers 3
Beta function (B) 130
Cauchy, A.L. 4
Chebychev, P. 6 7
Cohomology theory 83
Computations 56—57 74
Convolution 118 123
Critical line 22 67
Curve Jacobian of 83—85
Curve over a finite field 75ff
Curve place of 76—78
Curve point of 78
Davenport, H. 56
Dirichlet integral 113
Dirichlet, P.G.L. 2 30 113 115
Distributions 18
Divisor functions 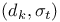 9—10 31—32 9—10 31—32
Eisenstein, G. 12
Euclid 2
Euler constant 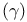 3 34 131—132 3 34 131—132
Euler function 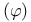 9 9
Euler product 1—2 33 35 38—39 86—87
Euler, L. 1—4
Explicit formulae of prime number theory 6 38—39 43 44 79—80 85
Ferrar, W. 25
Finite field 76
Fourier integral 117
Fourier series 115 116
Fourier transform 116 117
Frobenius map 82 83
Function field 76
Gamma function 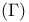 4 130ff 4 130ff
Gamma function, product representation 131
Gauss, C.F. 6 7
Grothendieck, A. 83
Hadamard product 31—35
Hadamard, J. 7 31 50 90 141
Hardy, G.H. 8 75
Hasse, H. 76
Heath-Brown, D.R. 64 110
Integral function 138—139
Integral function, order of 139
Integral means of the zeta-function 59—64 68—69 97
Iwasawa theory 4 58
Legendre — Jacobi symbol 109
Legendre, A.M. 7
Lindeloef hypothesis 67—72
Littlewood, J.E. 8 59—60
Local functional equation 18
Logarithmic integral (Li) 6
| Matsumoto, H. 86
Maximum principle, extended 142
Mellin transform 6 15 122ff
Moebius function 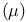 9 49 9 49
Multi-set 33
Numbers, l-adic 83
Partial summation 53
Perron’s formula 44 123
Prime numbers 1 2 5—9 38 44 51—53 72—75
Ramanujan, S. 49
Riemann hypothesis 5 7 67 70 72—76 80—82 86—87
Riemann Hypothesis, Weil’s criterion 80—82
Riemann — Lebesgue lemma 111
Riemann — Siegel formula 91
Riemann, B. 4—9 22 55 91
Schmidt, F.K. 76
Selberg trace formula 79 137
Selberg, A. 22 48 79
Set with multiplications 33
Siegel, C.L. 8 9 91
Stepanov, S.A. 76
Stirling’s formula 22 133 134
Summation formula, Euler — Maclaurin 30
Summation formula, Poisson 14 25—26 108 118—119
Summation Formula, Voronoi 14 25 32
Tate’s thesis 18
Theorems, Backlund 149—151
Theorems, Bohr — Landau 59
Theorems, Davenport — Hasse 89
Theorems, Hadamard’s "Three Circles" 71 143
Theorems, Hardy — Selberg 75
Theorems, Jensen 70 138
Theorems, Littlewood 60 148
Theorems, Phragmen — Lindeloef 23 68 143 144
Theorems, Plancherel 117
Theorems, Prime Number 6 7 51—53
Theorems, Riemann Mapping 144
Theorems, Riemann — Roch 79
Theorems, Wiener — Ikehara 51
Type of a function 15 122
v. Mangoldt function (A) 9
v. Mangoldt, H. 7 55
v.d. Corput, J.G. 100
Variation 111—113
Variation, function of bounded 111
Variation, function of total bounded 111
Vinogradov, I.M. 8 65
Weierstrass, K. 141
Weil, A. 76 78 80 82 84
Weyl, H. 102
Zero set of Riemann zeta-functic 5 33 50
Zeta-function of curve over a finite field 78
Zeta-function, functional equation 4 19
Zeta-function, integral representation 17 23
Zeta-function, p-adic 4 85
Zeta-function, Riemann 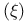 1ff 1ff
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте