|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Suzuki M. — Group Theory I |
|
|
 |
| Предметный указатель |
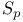 -subgroup 95 191 -subgroup 95 191
 -(sub) group 114 -(sub) group 114
 -homomorphism 115 -homomorphism 115
 -invariant 114 -invariant 114
 -isomorphism 115 -isomorphism 115
 -subgroup 92 -subgroup 92
 -component 101 -component 101
 -element 101 -element 101
 -group 101 -group 101
 -number 101 -number 101
(B,N)-pair 327
Abelian group 6 144
Abelian group, multiplier of an abelian group 265
Abelian group, torsion-free abelian group 280
Action (on a G-set) 60
Action (on a group) 66 114
Action induced action 71
Additive group 7
adjacency 318
Alternating form 335
Alternating group 293—308
Anti-Hopfian group 54
Apartment 319
Ascending chain condition 125
ASSOCIATED 195 263
Associative law 2
Associative law, general associative law 5
Automorphism 46
Baer 14 233 250 285
Baer sum of extensions 224
Bar resolution 205
Bar-convention 32
Base group of a wreath product 269
Basis Theorem of Burnside 93
Baumslag 278
Bender 105
Bilinear form of a Coxeter system 350
Branch point 364
Brauer 113
Bruhat decomposition 334
Building 319
Burnside 93 105 309
Canonical basis of Chevalley 385
Canonical homomorphism 36
Canonical induced action 71
Canonical mapping 31 166
Canonical representation of a Coxeter system 352
Cauchy 97
Cayley 58
Center 14
Center, i-th center 89
Central extension 246
Central product 137 139
centralizer 13
Chamber 319
Chamber complex 318
Characteristic series 116
Characteristic subgroup 50
Chevalley group 386
Chevalley group of exceptional type 387
Chief series 90
Class equation 63
Class of a nilpotent group 89
Class of a nilpotent group, conjugacy class 12
Classical group 370
Coboundary, cochain, cocycle 207
Cohomology dimension 220
Cohomology group 203
Cohomology group (of a subgroup) 207 213
Cohomology group (of cyclic groups) 220
Cohomology group (of free groups) 218
Cohomology group, (one-dimensional) 207
Cohomology group, (three-dimensional) 223
Cohomology group, (two-dimensional) 201 207
Cohomology group, applications 230
Collineation 31 311
Commutative 6
Commutative diagram 198
Commutative, general commutative law 6
Commutator 28 119
Commutator, commutator subgroup 119
Commute elementwise 52
Complement 230
Complete direct product 134
Complete group 56
Complete wreath product 270
Completely decomposable 135
COMPLEX 317
Complex, complex of rank d 318
Complex, thin complex, thick complex 318
Composite viii
Composition factor 43
Composition of mappings viii
Composition series 43 (see also “Characteristic series”)
Composition subgroup 45
Congruence x
Conjugacy class 12
conjugate 12
Conjugate, conjugate subgroup 14
Conjugate, the number of conjugates 22
Conjugation 46
Connectedness 313 318
Connectedness, (of graph) 349
Conway 391
Core 65
Corestriction 208 224
Correspondence theorem 32 40
Coset 19
Coset enumeration 174
Coxeter 173 340
Coxeter group (system) 340
Coxeter group (system), finite Coxeter system 359 369
Crossed homomorphism 207 243
Cycle decomposition of a permutation 292
Cyclic group 16
Cyclic group, automorphism group 49
Cyclic group, cohomology groups 220
Cyclic group, direct sum of cyclic groups 148 151 163—4
Dedekind law 26
Defining relations 165
Defining relations (of a subgroup) 188
Defining relations, examples 165 173 178 259 297—8 340
Derivation 207
Derived scries, derived subgroup 119
Dickson’s theorem 409
Dihedral group 8 173
Dimension of a projective subspace 310
Direct factor 127
Direct power 276
Direct product 70 127 129 134
Direct sum, direct summand 144
Directly (in-) decomposable 129
Distance 319
Divisible group 148 278
Division theorem ix
Domain of transitivity 64
Double coset 23
Doubly transitive see “K-transitive (k=2) ”
Eckmann — Gaschlitz Theorem 209
EDGE 347
Elemcntwise commutative 52
Elementary Abelian group 159
Endomorphism 52
Endomorphism ring 53
Epimorphism 35
Equivalent extension 199
Euler function 21
Even permutation 293
Exact sequence 198
Exchange condition 342
| Extension 192
Extension, central extension 246
Extension, extension and cohomology 201 232 233
Extension, split extension 230
Factor group 31
Factor set 193
Faithful 158
Feit — Thompson 188 237
Fermat 21
Field x
Finite field xii
Finite group 6
Finite group, finite Coxeter groups 347
Finite group, finite subgroups of SL(2,F) 404
Finitely generated 66
Finitely presented 189
Fischer 391
Flag (space) 313
Folding 322
Frame 311
Frattini subgroup 92
Free Abelian group 150
Free central extension 248
Free group 166
Free group, cohomology of a free group 218
Free group, standard form of an element 169
Free group, Subgroup Theorem 182
Free module 202
Free on a set 149 166
Free product (with amalgamation) 186
Free resolution 202
Free subset 160 280
Frobenius 112
Fully invariant 52
G-invariant (subgroup) 71
G-invariant (subset) 60
G-set 59
Gallagher 59 98
gallery 319
Gaschuetz 209 232 239 244 256
General associative law 5
General commutative law 6
General linear group 73
General wreath product 272
Generalized quaternion group 259
Generate 12
Generated freely 150 166
Generating set 12
Generating set, a generating set of a subgroup 180
Generator 12
Generator, generators and relations 164
Geometry of linear groups 310
Glauberman 244
Goldschmidt 105
Gorenstein 392
Graph 347
Graph, graph of finite irreducible Coxeter groups 359
Green 261
Griess 391
Group 2
Group defined by a set of generators and relations 165
Group of automorphisms 46
Group of automorphisms (of a p-group) 93 239
Group of automorphisms (of the alternating group) 299 301
Group of automorphisms (of the alternating group, degree 6) 299 301
Group of automorphisms (of the symmetric group) 300
Group of automorphisms, examples 49 83 161 325 332
Group of inner automorphisms 47
Group of order 168 107
Group of order p*q 103 104
Group ring over  201 201
Group theoretical property 38
Group, abelian group 6 144 280
Group, cyclic group 16
Group, dihedral group 8 173
Group, finite group 6
Group, free group 166
Group, infinite group 6
Group, nilpotent group 89
Group, permutation group 58
Group, solvable group 118
Group, symmetric group 57 291
Hall, M. 106 390
Hall, P. 86 93 106 237 256 279
Harada 391
Height 282
Held 391
Hermitian form 371
Higman, D. G. 244 391
Higman, G. 59 178 189 192 245 278 390 391
Hirsch 122 126
Hochschild — Serre Theorem 213
Homomorphic image see “Factor group”
Homomorphism 35
Homomorphism theorem 38 115
Homomorphism, operator homomorphism 115
Hyperplane 76
i-th center 89
Identity 4
Identity matrix 7
Indecomposable 129
Independent 129 134 311
INDEX 16
Induced action 71 114
Inductive set xi
Infinite group 6
Inflation mapping 213
Injective Abelian group 162
Inner automorphism 46
Internal direct product 129
Internal semidirect product 69
Intersection 11
Invariant 60 371
Invariants of an Abelian group 147
Inverse 4
Irreducible action 72 158
Irreducible central extension 252
Irreducible Coxeter system 350
Isoclinism 256
Isomorphic scries 117
Isomorphism 35
Isomorphism class 35
Isomorphism Theorem (First) 41
Isomorphism Theorem (for  -groups) 115 -groups) 115
Isomorphism Theorem (Second) 42
Isotropic 378 382
Iwasawa 81 339
Janko 390 391
Jonsson 287
Jordan — Hoelder theorem 43 117
k-transitive 312
Kaloujnine — Krasner Theorem 272
Kernel 35
Krull — Remak — Schmidt Theorem 131
Lagrange 21
Left coset 16
Length of a gallery 319
Length of a series 114
Length of an clement of a Weyl group 329
Length of an orbit 60
Leon 391
Lie type 387
Lifting 246
Linear group 73
Linear group, geometry of linear groups 310
Linearly ordered xi 18
Lyndon 216 228
Lyons 391
Mathieu group 390
Matrix representing a form 372
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



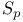 -subgroup
-subgroup  -(sub) group
-(sub) group  -subgroup
-subgroup  -component
-component