|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Sapidis N.S. — Designing Fair Curves and Surfaces: Shape Quality in Geometric Modeling and Computer-Aided Design |
|
|
 |
| Предметный указатель |
Airfoil curve, leading edge 37 38
Airfoil curve, smoothing the curvature of 38 43
Almost rational spline 32
Automatic fairing, of spline curves 45
Automatic fairing, point sets in 45
Automatic fairing, problem 86
Automotive design, exterior 3 17 26 232
Averaging, Doo Sabin algorithm for 279
Averaging, mask 282
Bezier curves 79 87 90 93 94
Bezier patch 110 119
Bezier patch, convex combination of 297 300
Bezier patch, rational 297
Blend, extended 240
Blend, PDE 210
Blend, ratio 278 291
boundary conditions 233 237 211
Boundary conditions, derivative 212
Boundary conditions, function 242
Boundary-value technique 232
Circular splines, basic facts of 21
Circular splines, computation of 22—24
Circular splines, discretization using 18—21
Computer-aided design 29
Constrained optimization 79 89
Constrained optimization as a basis for curve smoothing 32 34—36
Constrained optimization, geometrical and smoothness constraints in 30
Continuity by penalty 142
Continuity, tangent 142
Continuity, tangent plane 242 283
contour 306 310
Control matrices, for positional patches 298
Control patterns, planar 296 298 299 300 308
Control patterns, planar, construction of 306—307
Control polygon 61
Convex combination, of Bezier patches 297 300
Convex hull 61 62 64 67 300
Convex hull, of spheres 163 172
Convex set, extreme points of 62—63 67 70
Convexity 162 201—207
Convexity, local 202
Convexity, proof of 205 207
Convexity-preserving spline 257
Convolution kernel 296 297
Convolution surface 296 297
Corner-cutting 277
Corner-cutting control pattern 306
Cornu spiral 31
Cubic spline 76—77
Cubic spline, 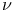 -spline 77—78 -spline 77—78
Cubic spline, minimum property of 77—79
Curvature 129 161 207 209 see
Curvature, constrained optimization problem of 62 68
Curvature, constraints on area under curve 79
Curvature, constraints, computing circular splines with 18—27
Curvature, continuity at a vertex 146
Curvature, continuum methods of 143
Curvature, control problem 255
Curvature, convexity 32
Curvature, convexity, alpha convexity 16—18
Curvature, convexity, conditions of 12 13 17
Curvature, convexity, intrinsic parameters of 14—15
Curvature, empirical properties of 12
Curvature, empirical properties of, maxima and minima of 4 8
Curvature, Gaussian 146 149 150
Curvature, maximum absolute 291
Curvature, mean 146 253
Curvature, monotonicity of 8—11
Curvature, numerical 21 24
Curvature, optimization of 10 18 62 68
Curvature, principal 124
Curvature, principal, least squares fit of 136—138
Curvature, principal, lines of 140
Curvature, tensor 141
Curve fitting, aesthetic constraints of 3—27
Curve fitting, aesthetic constraints of, analysis using parametric representations 5
Curve fitting, intrinsic equation of 4 7—8
Curve fitting, problem 4
Curve fitting, smoothing 26—27
Curve fitting, use of styling radius for 11
Cusp-free surfaces 202—203
Cyclide 162 163f 175 178f 185 186f
Cyclide, Dupin 175—177
Cyclide, edge 184—185
Design, concept 231
Design, engineering 231
Design, free-form 236
Design, interactive 234 239—246
Design, interactive free-form 246—248
Design, real-time 241
Designer's intuition 161 209
Difference geometry of polygons 46—50
Difference geometry of polygons, arc length 46
Difference geometry of polygons, chord length parameterization 46
Difference geometry of polygons, closed 46
Difference geometry of polygons, derivatives of 49
Difference geometry of polygons, discrete curvature 46 47
Difference geometry of polygons, discrete Frenet frame 47
Difference geometry of polygons, discrete Frenet — Serret frame 47
Difference geometry of polygons, discrete torsion 47
Difference geometry of polygons, euclidean invariants 49
Difference geometry of polygons, inflection points 49
Difference geometry of polygons, open 46
Difference geometry of polygons, osculating planes 48
Difference geometry of polygons, rigid body motions 49
Discrete Curvature Method 53
Discrete Curvature-Torsion Method 56
Discrete Frenet frame 47
Discrete Frenet — Serret frame 47
Facet spheres 172—175
Facet spheres, bounds on the radii of 187—201
Faired curves 75—120
Faired curves, curvature plot 79
Faired curves, curvature plot, fairness metrics 80—86
Faired curves, fairness metrics and derived curves 82 83
Faired curves, fairness metrics and design curves 82 83
Faired curves, fairness metrics, algorithms for 86—87 95
Faired curves, fairness metrics, arc length 81 87 94 95
Faired curves, fairness metrics, centers of spherical curvature 84
Faired curves, fairness metrics, flattening 84
Faired curves, fairness metrics, Frenet — Serret formulas an 81 83 85
Faired curves, fairness metrics, geometric invariants 81 87
Faired curves, fairness metrics, implementation of 86—104
Faired curves, fairness metrics, planar evolute 90
Faired curves, fairness metrics, radius of spherical curvature 84
Faired curves, fairness metrics, rounding 84
Faired curves, fairness metrics, smoothing 84
Faired curves, fairness metrics, total variation 89
Faired curves, smoothness 83
Faired curves, variational methods 78
Fairing problem 253
Fairness criteria 254
Fairness criteria for curves 76 78
Fairness criteria for curves, discrete 50
Fairness criteria for curves, global 50
Fairness criteria for curves, local 50
Fairness criteria for curves, metrics 80—86
Fairness criteria for curves, metrics, implementation of 86—104
Fairness metrics for curves 80—86
Fairness metrics for curves, adaptive quadrature in 87
Fairness metrics for curves, algorithms for 86—87 95
Fairness metrics for curves, examples 95—104
Fairness metrics for curves, implementation of 86—104
Fairness metrics for curves, software engineering and 81—93
Fairness metrics for curves, total variation 89
Fairness metrics for curves, total variation, for monotone curvature 89—90 93
Fairness metrics for curves, typical problem in 87
Fairness metrics for surfaces 104—119
Fairness metrics for surfaces, algorithm for 109—110
Fairness metrics for surfaces, derived surface 105
| Fairness metrics for surfaces, flattening 106 107 110—119
Fairness metrics for surfaces, Gaussian curvature 105 110—119
Fairness metrics for surfaces, geometric invariants 104 105
Fairness metrics for surfaces, mean curvature 105 110—119
Fairness metrics for surfaces, principal curvature 105
Fairness metrics for surfaces, rolling 106 108 110—119
Fairness metrics for surfaces, rounding 106 107—108 110—119
Fairness metrics for surfaces, surface area 105
Feasible polygon 63 65
Feasible polygon, inflection segment of 63 65 66 68
Finite element analysis, of smooth surfaces 128
Fresnel integral 31
Gauss map 205—206
Gaussian curvature 146
Gaussian curvature, functional offset surfaces in 150
Geometric primitive 296 297
Hermite curves 129
Highlight bands, application examples, discontinuity magnification 217 219f—220f
Highlight bands, application examples, irregularity detection 217 220 221f—223f
Highlight bands, application examples, real time manipulation 220
Highlight bands, computational algorithm, basic steps of 221 224
Highlight bands, computational algorithm, exhaustive search method 221
Highlight bands, computational algorithm, principles of 221
Highlight bands, computational algorithm, resolution, choices of 224
Highlight bands, defined 215
Highlight bands, graphical representation 215—216
Highlight bands, optimal performing code, code decomposition 226 227f
Highlight bands, optimal performing code, floating point operations, analysis of 225—226
Highlight bands, optimal performing code, global results 227—228 228f
Highlight bands, optimal performing code, vector and parallel processing 226—227
Highlight bands, properties, band shape, manifestation of 216—217 218f—219f
Highlight bands, properties, band width, manifestation of 215—216 217f
Highlight lines, defined 214—215
Highlight lines, model of 214
Interpolation, interpolation curves 132
Interpolation, inversion, of surfaces 177—183 185
Interpolation, of points 282
Interpolation, surfaces 161 193—399
Isophote patterns 307
Krein — Milman, theorem of 63
Linear curves, piecewise 61
Linear curves, rough and fine fairing of 62 66 69 70
Lines of principal curvature 140
Lines of reflection 149
Mesh, irregular 279
Mesh, of points 277
Mesh, refinement 279 283
Mesh, regular 277 279
Minimization, of fairness functionals 131
Minimum energy curve (MEC) 126
Minimum energy curve (MEC), comparison with MVC and natural splines 147
Minimum energy curve (MEC), definition 123
Minimum energy curve (MEC), space curves 149
Minimum norm networks 127
Minimum variation curve (MVC) and nonlinear splines 126—127
Minimum variation curve (MVC), calculation of 133
Minimum variation curve (MVC), comparison with natural spline and MEC 147
Minimum variation curve (MVC), computation of 128
Minimum variation curve (MVC), convexity preserving 123
Minimum variation curve (MVC), existence and uniqueness of 133
Minimum variation curve (MVC), functional of 130
Minimum variation curve (MVC), initialization for minimization 132
Minimum variation curve (MVC), previous work on 126—127
Minimum variation curve (MVC), space curves 149
Minimum variation curve (MVC), specification of 124 125f
Minimum variation networks (MVN), computation of 135
Minimum variation networks (MVN), continuity of 135
Minimum variation networks (MVN), initialization for minimization 136
Minimum variation networks (MVN), optional continuity constraints 138 139f
Minimum variation networks (MVN), previous work on 127
Minimum variation networks (MVN), representation of 135
Minimum variation surface (MVS), computation of 138
Minimum variation surface (MVS), continuity of penalty 142
Minimum variation surface (MVS), functional of 140
Minimum variation surface (MVS), initialization for minimization 144
Minimum variation surface (MVS), optimization of 153
Minimum variation surface (MVS), tangent continuity and 142
Mouse, use in interactive design 237 241
N-sided patches 297—300
N-sided patches, four-sided subpatch 296
N-sided patches, homogeneous 295
N-sided patches, normal continuity for 300—304
Natural spline, comparison with MVC and MEC 147
Nonlinear optimization 128
Nonlinear splines 127
Nonuniform degree, polynomial splines of 253 255—259
Norm, of a spline curve 32
Offending node 254
Optimization problem, constrained 62 68
Optimization, constrained 79 89
Optimization, constrained, as a basis for curve smoothing 32 34
Optimization, constrained, geometrical and smoothness constrain in 30
Optimization, constrained, nonlinear 128
Optimization, constrained, of smooth surfaces 128 248
Parallel processing, application of see "Highlight bands"
Parametrization 235 242 248
Patch, bicubic 278 280 282 285 289
Patch, degenerate 295
Patch, N-sided 297—304
Patch, polynomial 297
Patch, positional 296 297 298
Patch, rational 282
Patch, weight 296 297 302
PDE blends 240
PDE method 232 233—236
Piecewise linear curves 61
Piecewise linear curves, rough and fine fairing of 62 66 68 70
Planar fairing algorithm 51—54
Planar fairing algorithm and distance tolerance 53
Planar fairing algorithm and shape preservation 59
Planar fairing algorithm and stability 59
Planar fairing algorithm, Discrete Curvature Method 53
Planar fairing algorithm, nonlinear optimization 53
Plane curves, differential geometry of 5
Plane curves, differential geometry of, analysis using parametric representations 5
Plane curves, differential geometry of, arc length 5
Plane curves, differential geometry of, curvature of 7
Plane curves, differential geometry of, curvature of, bulk distribution of 30 41
Plane curves, differential geometry of, curvature of, denominator of 33
Plane curves, differential geometry of, curvature of, high and low frequency features of 30
Plane curves, differential geometry of, curvature of, modification of 29
Plane curves, differential geometry of, curvature of, monotone 33 37 39
Plane curves, differential geometry of, curvature of, nonnegative 33
Plane curves, differential geometry of, curvature of, numerator of 33
Plane curves, differential geometry of, curvature of, profile 30 38f 43f
Plane curves, differential geometry of, curvature of, slope numerator of 34
Plane curves, differential geometry of, intrinsic condition 8
Plane curves, differential geometry of, intrinsic equation 7—8
Plane curves, differential geometry of, tangent angle of 6
Principal curvature, definition of 124
Principal curvature, least squares fit of 136—138
Principal curvature, lines of 140
Principal direction, definition of 124
Principal direction, least squares fit of 136—138
Principle of simplest shape 4
Reparametrization 278 283
Shape parameter 278
Shape-preserving interpolation problem 253
Space curve 149
Spatial fairing algorithm 54—58
Spatial fairing algorithm, Discrete Curvature — Torsion Method 56
Spline curve, 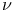 -spline 77—78 -spline 77—78
Spline curve, automatic fairing of 45
Spline curve, B-spline 79 91
Spline curve, Bezier 79 87 90
Spline curve, cubic interpolatory 76 79
Spline curve, fairness metrics and 91
Spline curve, natural 147
Spline curve, nonlinear 127
Spline curve, norm of 32
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



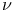 -spline
-spline