Авторизация
Поиск по указателям
Schmidt K. — Dynamical systems of algebraic origin
Обсудите книгу на научном форуме Нашли опечатку?
Название: Dynamical systems of algebraic originАвтор: Schmidt K. Аннотация: Although the study of dynamical systems is mainly concerned with single transformations and one-parameter flows (i.e. with actions of Z, N, M, or M+), er-godic theory inherits from statistical mechanics not only its name, but also an obligation to analyze spatially extended systems with multi-dimensional symmetry groups. However, the wealth of concrete and natural examples, which has contributed so much to the appeal and development of classical dynamics, is noticeably absent in this more general theory. A remarkable exception is provided by a class of geometric actions of (discrete subgroups of) semi-simple Lie groups, which have led to the discovery of one of the most striking new phenomena in multi-dimensional ergodic theory: under suitable circumstances orbit equivalence of such actions implies not only measurable conjugacy, but the conjugating map itself has to be extremely well behaved. Some of these rigidity properties are inherited by certain abelian subgroups of these groups, but the very special nature of the actions involved does not allow any general conjectures about actions of multi-dimensional abelian groups...
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1995Количество страниц: 320Добавлена в каталог: 23.10.2010Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
1 xvi 247 247 12 7 247 247 226 71 108 94 47 247 247 247 247 247 247 153 xvi 242 242 105 106 106 106 108 1 108 60 111 111 62 62 175 175 62 62 62 64 63 xvi 44 1 228 39 64 2 80 1 1 36 143 59 80 36 105 174 xvi 228 43 62 61 125 xvi xvi xvi 61 xvi xvi xvi xvi xvi xvi 35 173 196 35 285 173 105 293 47 114 8 169 162 18 18 201 153 270 270 109 162 222 162 290 269 62 144 270 242 242 242 234 234 162 2 43 59 59 49 35 36 37 231 235 235 243 243 243 43 43 108 30 Adele ring 62 adj(A) 91 Adjoint matrix 91 230 Algebraic number field 61 Algebraic unit 65 Almost block independent, sporadically 201 Almost block independent, universally 201 Almost box independent 201 Almost box independent, relatively 215 ann(a) 44 Annihilator 12 44 Arteen — Rees Lemma 49 Associated module 44 Associated prime ideal 44 Aut(X) 1 Automorphism see "Group automorphism" Bernoulli, factor 197 Bernoulli, measure 200 Bernoulli, shift 87 Borel sigma-algebra 2 C( 199 C(X) 1 Cech homology 42 Cellular automaton vii centralizer 12 char( 43 CHARACTER 2 Character, group 2 Characteristic 43 Characteristic, polynomial 37 Coboundary 293 Coboundary, algebraic 296 Cobounding function 293 Cocycle 293 Cocycle with summable variation 295 Cocycle, affine 295 Cocycle, algebraic 295 Cocycle, cohomologous 293 Cocycle, continuous 293 Cocycle, Hoelder 295 Cocycle, homomorphism 293 Cocycle, trivial 293 Completely positive entropy 162 Completion (w.r.t. a valuation) 61 Conditional entropy 108 Conditional expectation xvi Conditional information function 108 Conjugate, algebraically 2 Conjugate, measurably 2 Conjugate, to a full subshift 10 Conjugate, to a Lie subshift 10 Conjugate, to a subshift 10 Conjugate, topologically 2 Convolution 27 111 165 Coupling 199 Cyclotomic polynomial see "Polynomial" D.C.C. see "Descending chain condition" deg(f) 180 Descending chain condition 19 Dirichlet's L-function ix Dual 35 Dual action 18 Dual automorphism 2 Dual group 2 Dual homomorphism 2 Dual module 36 Entropy of a 108 Entropy of a 242 Entropy of a 106 Entropy of a partition 108 Entropy, completely positive 162 Entropy, completely positive, on a sigma-algebra 162 Entropy, conditional 108 Entropy, dimension 226 227 Ergodic 47 Ergodic group action by automorphisms 2 Ergodic group automorphism 2 Ergodic prime ideal 56 Ergodic probability measure 172 Ergodic subgroup 9 Expansive 114 Expansive group action by automorphisms 2 Expansive group automorphism 2 Expansive neighbourhood 2 Expansive prime ideal 56 Expansive subgroup 9 Extension problem 32 F(n) 29 Face (of a convex set) 153 231 First cohomology group 293 Fourier transform 193 Frac(r) 67 Fractional part 67 Free module 90 Free orbit 122 123 gcd(a) 229 Generator (of a sigma-algebra for a group action) 109 Generators (of a module) 37 Group action by automorphisms 2 Group action by automorphisms, (strongly) mixing 2 Group action by automorphisms, ergodic 2 Group action by automorphisms, expansive 2 Group action by automorphisms, measure preserving 2 Group action by automorphisms, topologically transitive 2 Group action, transitive 165 Group automorphism 1 Group automorphism, dual 2 Group automorphism, ergodic 2 Group automorphism, expansive 2 Group automorphism, inner 1 Group automorphism, mixing 2 Group automorphism, topologically transitive 2 Group automorphism, trivial 1 Group of Markov type 24 Group of units 69 Group, character 2 Group, compact 1 Group, compact, Lie 1 Group, cyclic 23 Group, dual 2 Group, Polish 293 Group, polycyclic-by-finite 24 Group, ring 27 Group, torsion 44 Group, torsion-free 39 44 h( 109 Haar measure 2 Highest common factor of an ideal 229 Hoelder function 295 Hoelder structure 294 Homomorphism, central 11 Homomorphism, dual 2 Ideal, maximal 70 Ideal, principal 37 Indicator function xvi Inn(X) 1 Int(r) 67 Integral part 67 Invariant metric 1 3 Invariant probability measure 2 111 Invariant subgroup 1 J( 199 Jensen's formula 126 joining 199 ker( 1 Kernel 1 Krull dimension 227 Laurent polynomial 35 Laurent polynomial, nice 206 Ledrappier's example viii Lehmer's problem 161 Lie subshift 10 Livshitz' theorem 294 Logarithmic height 137 Mahler measure 125 Markov subgroup 81 Markov type 24 Maximal compact subring 62 Measure of maximal entropy 195 Measure preserving, 108 Measure preserving, group action by automorphisms 2 Measure preserving, isomorphism 2 Mixing, 8 Mixing, group action by automorphisms 2 Mixing, group automorphism 2 Mixing, of all orders 262 Mixing, of order n see "n-mixing" Mixing, prime ideal 56 Mixing, probability measure 285 Mixing, subgroup 9 Module, associated 44 Module, cyclic 38 Module, free 90 Module, Noetherian 28 37 Module, torsion 44 Monomial 80 Morse sequence 291
Реклама
 |
|
О проекте
|
|
О проекте



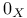 ,
, 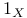 , 0, 1
, 0, 1 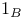
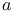
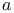
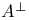
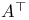
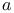
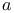
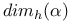
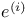
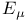
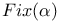
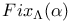
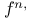
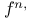
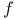
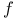
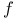
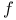
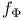
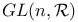
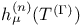
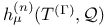
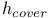
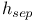
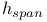
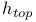
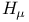
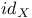
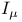
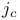
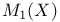
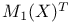
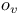
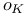
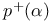
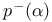
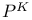
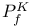
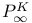
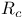
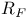
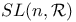
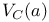
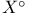
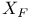
 -periodic point
-periodic point 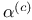
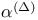
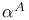
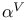
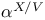
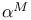
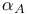
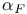
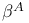
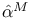
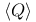
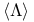

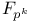
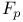
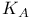
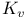
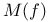
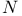
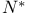

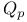

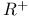
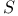
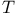

![$\mathbb{Z}[\frac{1}{n}]$](/math_tex/f02584a41834cebfdf328429b1acd1f982.gif)
![$\mathbb{Z}[\mathbb{Z}^{d}]$](/math_tex/5bc89a64bf5b1f094f674cbcce887e8782.gif)
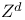 -action, aperiodic
-action, aperiodic 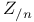
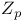
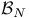
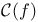
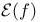
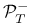
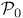
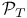
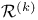
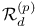
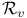
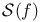
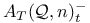
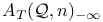
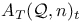
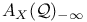
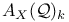
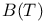
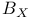

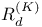

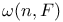
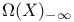
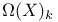
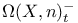
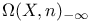
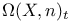
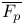
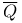
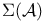
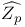
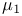 ,
,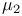 )
) 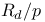 )
)