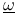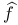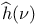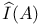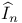|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Hollander Fr. — Large deviations |
|
|
 |
| Предметный указатель |
 III.1 III.1
 III.5 III.5
 I.1 I.3 II.1 IV.1 VI.1 VII.1 I.1 I.3 II.1 IV.1 VI.1 VII.1
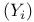 III.5 IV.1 III.5 IV.1
 X.6 X.6
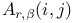 IX.7 IX.7
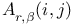 IX.9 IX.9
 IX.6 IX.6
 IX.9 IX.9
 X.6 X.6
 II.1 II.1
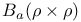 II.2 II.2
 II.5 II.5
 II.5 II.5
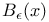 III.1 III.1
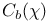 III.2 III.2
 VIII.4 VIII.4
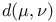 II.1 II.2 II.5 II.7 II.1 II.2 II.5 II.7
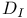 I.3 I.3
 II.5 II.5
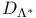 V.2 V.2
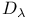 V.1 V.1
 I.4 I.4
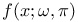 X.1 X.1
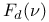 VIII.6 VIII.6
 IX.6 IX.6
 IX.9 IX.9
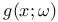 X.1 X.1
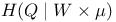 X.3 X.3
 II.2 II.5 II.2 II.5
 II.1 II.1
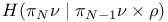 II.5 II.5
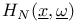 X.1 X.1
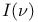 VIII.2 VIII.2
 VII.2 VII.2
 VI.2 VI.2
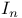 IX.1 IX.1
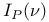 IV.2 IV.2
 IV.2 IV.2
 IV.3 IV.3
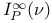 IV.3 IV.3
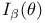 IX.9 IX.9
 II.1 II.7 II.1 II.7
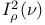 II.2 II.2
 II.5 II.5
 II.5 II.5
 VIII.2 VIII.2
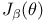 , , 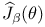 IX.3 IX.3
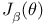 IX.9 IX.9
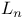 I.1 II.1 I.1 II.1
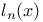 IX.2 IX.2
![$L_{N}(\underline{x}[0,T],\underline{\omega})$](/math_tex/5de4d9a707d67b932dda9720dc073d0282.gif) X.2 X.2
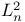 II.2 II.2
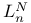 II.5 II.5
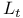 IV.4 IV.4
 VIII.5 VIII.5
 X.4 X.4
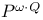 X.4 X.4
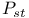 IV.1 IV.1
 IX.5 IX.5
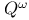 X.5 X.5
 X.5 X.5
 X.5 X.5
 X.5 X.5
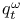 X.5 X.5
 IX.9 IX.9
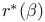 IX.8 IX.8
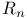 II.5 II.5
 IX.7 IX.7
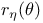 VII.7 VII.7
 I.1 I.3 IX.1 I.1 I.3 IX.1
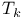 VII.3 VII.3
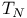 VIII.4 VIII.4
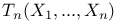 VI.1 VI.1
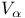 VII.1 VII.1
 VIII.3 VIII.3
 VIII.4 VIII.4
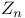 V.1 V.1
 VII.1 VII.1
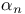 VI.1 VI.1
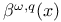 X.4 X.4
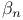 VI.1 VI.1
 III.1 III.1
 VIII.3 VIII.3
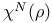 , ,  VIII.5 VIII.5
 IX.3 IX.3
 IX.4 IX.4
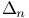 VI.1 VI.1
 VII.7 VII.7
 II.1 II.1
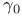 , , 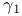 VI.1 VI.1
 X.1 X.1
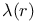 VII.3 VII.3
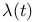 V.1 V.1
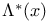 V.1 V.1
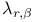 IX.7 IX.7
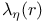 VII.7 VII.7
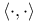 IV.4 V.1 IV.4 V.1
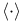 VII.1 VIII.1 VII.1 VIII.1
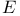 I.1 I.1
 VIII.1 VIII.1
 VII.1 VII.1
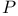 I.1 III.7 V.1 VI.1 VII.1 I.1 III.7 V.1 VI.1 VII.1
 , , 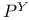 IV.1 IV.1
 X.1 X.1
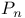 IX.1 IX.1
 VIII.1 VIII.1
 VII.1 VII.1
 IX.1 IX.1
 X.3 X.3
 X.1 X.1
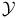 III.5 III.5
 II.1 II.1
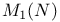 II.7 II.7
 I.1 I.3 II.1 II.2 II.5 II.7 X.1 I.1 I.3 II.1 II.2 II.5 II.7 X.1
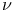 II.1 II.2 II.5 II.7 II.1 II.2 II.5 II.7
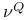 X.5 X.5
 VII.1 VII.1
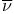 II.2 II.5 II.2 II.5
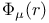 X.6 X.6
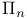 II.5 II.7 II.5 II.7
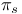 IV.1 IV.1
 X.4 X.4
 II.1 VIII.1 II.1 VIII.1
 VII.1 VII.1
 I.1 I.3 II.5 I.1 I.3 II.5
 IX.10 IX.10
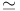 I.1 I.1
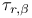 IX.7 IX.7
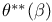 IX.9 IX.9
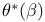 IX.2 IX.2
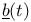 X.1 X.1
![$\underline{b}[0,T]$](/math_tex/57e8a3c07ae2cf81d57fe9f45c73888182.gif) X.1 X.1
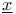 X.1 X.1
 X.1 X.1
![$\underline{x}[0,T]$](/math_tex/64e49cf9b4154050f9346520b0f9ee3482.gif) X.1 X.1
| 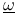 X.1 X.1
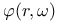 VII.3 VII.3
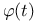 I.3 I.3
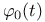 VI.2 VI.2
 V.1 V.1
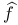 I.3 I.3
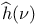 II.6 II.6
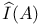 III.7 III.7
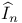 IX.2 IX.2
 IX.9 IX.9
 IX.3 IX.3
 IV.4 IV.4
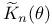 IX.4 IX.4
 II.2 II.2
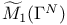 II.5 II.5
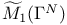 II.5 II.5
 VII.3 VII.3
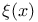 VIII.1 VIII.1
Affine II.2
Annealed measure VII.8
Bridge IX.3
Brownian motion X.1
Closure III.1
CLT I.1
Continuous, map III.5
Contraction principle, general III.5
Contraction principle, Sanov — Cramer II.4
Contraction, by linear transformation III.7
Convex, hull III.7
Convex, locally III.7
Correlation coefficient VIII.4
Decision test, Neyman — Pearson VI.1
Diffusion X.1
Dirichlet form IV.4
Distance, Euclidean V.1
Distance, myopic total variation II.5
Distance, on Polish space III.1
Distance, total variation II.1 II.2 II.5 II.7
e V.2
Empirical average I.3
Empirical double layer measure X.2
Empirical measure II.1 II.7
Empirical measure, N-word II.5
Empirical measure, pair II.2
Empirical process II.5
Entropy, relative II.1 II.2 II.5
Entropy, relative, specific II.6
Euler circuit II.2
Exposed, hyperplane V.1
Exposed, point V.1
f I.3 III.2 III.3 IV.1
F(Q) X.2
Feynman — Kac formula VIII.1
Function, affine II.2 II.5 IV.2
Function, convex III.7
Function, cumulant generating I.3
Function, exponential integral of III.3 III.4
Function, lower semi-continuous I.3 III.1
Function, moment generating I.3
Function, rate I.1 III.1
Function, steep I.4 V.2
G IV.4
Gibbs measure X.1
H(t) VIII.1
Hamiltonian X.1
Hitting time VII.3
I(Q) X.3
I(S) III.1
i(x) III.1
I(z) I.3
I-continuous III.2
int, cl III.1
Interior III.1
Intermittency VIII.2
J(u) VII.3
J(y) III.5
Kuramoto model X.6
L(X) IX.4
Ldp III.1
LDP, weak III.6
Local time VIII.5 IX.2 IX.4
Locally convex III.7
Logarithmically equivalent I.1
Lower semi-continuous I.3 III.1
m(X) IX.5
Markov chain, continuous-time IV.4
Markov chain, discrete-time IV.2
Markov chain, generator IV.4
Markov chain, reversible IV.4
Markov chain, stationary IV.1
Markov chain, transition kernel IV.1
McKean — Vlasov equation X.5
Measure, ergodic II.6
Measure, exponentially tight family III.2
Measure, occupation time IV.3
Parabolic Anderson model VIII.1
Perron — Frobenius IV.3 V.4 IX.7
Polish space II.1 III.1
Polymer IX.1
q X.4
Quenched measure VII.8
R VII.3 IX.7 X.6
Random, bridge IX.3
Random, continued fractions VII.5
Random, drift VII.1 X.4
Random, homogeneous walk VII.7
Random, medium VIII.1
Random, simple VIII.1 IX.1
Random, walk in random environment VII.1
Random, walk, self-repellent IX.1
Relative interior V.2
rint V.2
Set, closed III.1
Set, compact III.1 III.6
Set, continuity III.2
Set, level I.3 III.1
Set, open III.1
Set, relative interior V.2
SLLN I.1
Speed VII.2 IX.2
Stirling's formula I.2
Subadditive sequence III.7
t III.5
Theorem, Birkhoff Ergodic II.2
Theorem, Bryc III.3 V.3
Theorem, Cramer I.3 I.4 I.5 II.4
Theorem, Gaertner — Ellis V.2
Theorem, Kolmogorov Extension II.5
Theorem, Sanov II.1 II.3 II.4
Theorem, Shannon — McMillan — Breiman II.6
Transform, Cramer I.3
Transform, Legendre I.4 V.1
u(x,t) VIII.1
Varadhan's lemma III.3
Varadhan's Lemma, inverse III.3
w X.1
Z(t) VIII.1
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте






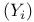

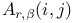









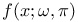
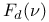


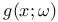
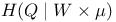










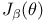 ,
, 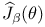
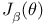
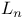
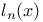
![$L_{N}(\underline{x}[0,T],\underline{\omega})$](/math_tex/5de4d9a707d67b932dda9720dc073d0282.gif)
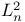
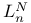
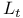


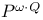
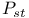

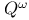



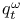

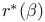
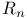

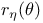

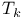
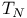
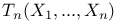
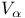


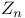

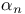
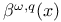
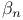


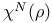 ,
, 


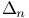


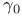 ,
, 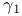

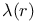
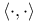
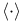
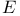


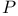
 ,
, 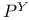

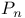





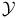

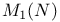







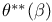
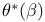
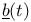
![$\underline{b}[0,T]$](/math_tex/57e8a3c07ae2cf81d57fe9f45c73888182.gif)
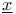

![$\underline{x}[0,T]$](/math_tex/64e49cf9b4154050f9346520b0f9ee3482.gif)