|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Berge C. — The Theory of Graphs |
|
|
 |
| Предметный указатель |
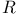 , space of real numbers p. 2 , space of real numbers p. 2
Ancestor p. 11
Antinode p. 123
Arborescence p. 13
ARC p. 6
Articulation, point p. 196
Articulation, set p. 203
Associated number of a vertex p. 119
Basis, of a graph p. 13
Basis, of a vector spaoe p. 28
Bound (of a set), upper, lower p. 13
Branch p. 123
Capacity, in a network p. 71
Capacity, of a graph p. 39
Centre p. 119
Chain,  , simple, composite p. 9 , simple, composite p. 9
Chain, alter- nating p. 171
Chain, Eulerian p. 166
Chain, Hamiltonian p. 187
Circuit,  , elementary p. 7 , elementary p. 7
Circuit, Eulerian p.167
Circuit, Hamiltonian p. 107
CLIQUE p. 36
Closure, transitive p. 4
Coefficient, of external stability p. 40
Coefficient, of internal stability p. 36
Component p. 9
Cover, of a simple graph p. 77
Cover, of any graph p. 177
Cut p. 74
Cycle, Eulerian p. 166
Cycle, Hamiltonian p. 187
Cycle, independent p. 28
Cycle, simple, composite, elementary p. 9
Deficiency p. 96
Demi-degree, outward, inward p. 86
Descendant p. 11
Diameter p. 126
Distance between two vertices p. 196
Distance between two vertices, directed p. 119
EDGE p. 8
Equilibrium p. 60
Equivalence, 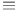 p. 3 p. 3
Equivalence, associated with a graph p. 11
Factor p. 111
Flow p. 71
Flow, complete p. 76
Function, characteristic p. 47
Function, composite p. 4
Function, Grundy function 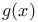 p. 22 p. 22
Function, ordinal function  p. 21 p. 21
Function, preference p. 68
Function, preserving p. 39
Function, single-valued, multivalued p. 3
Game p. 62
Game, partial p. 68
Graph,  p. 6 p. 6
Graph,  p. 6 p. 6
Graph,  -chromatic p. 30 -chromatic p. 30
Graph, 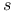 -graph p. 27 -graph p. 27
Graph,  -finite, -finite,  -finite, -finite,  -bounded p. 16 -bounded p. 16
Graph, antisymmetric, complete p. 8
Graph, biconnected p. 198
Graph, connected p. 9
Graph, dual p. 214
Graph, finite p. 16
Graph, inductive p. 13
Graph, locally finite p. 16
| Graph, partial p. 6
Graph, planar p. 30
Graph, progressively bounded, progressively finite p. 16
Graph, pseudo- symmetric p. 167
Graph, regressively bounded, regressively finite p. 17
Graph, simple p. 77
Graph, strongly connected, symmetric p. 8
Graph, total p. 12
Graph, totally inductive p. 14
Graph, transitive p. 12.
Image p. 4
Index, ohromatic p. 30
Intersection p. 2
Inverse p. 4
Kernel p. 46
Lattice property p. 13
Loop p. 7
Majorant p. 11
Matching, W, of a simple graph p. 92
Matching, W, of any graph p. 178.
Matrix, associated with a graph p. 130
Matrix, cyclomatic p. 149
Matrix, incidence matrix of the arcs, incidence matrix of the edges, the unimodular property p. 141
Maximum p. 12
Minimum p. 12
Minorant p. 12
Multiplication, logical p. 42
Network p. 71
Node p. 123
Number, chromatic 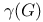 p. 30 p. 30
Number, cohesion 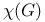 , connection , connection 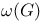 p. 203 p. 203
Number, cyclo- matic 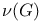 p. 27 p. 27
Number, ordinal, ordinal limit p. 20
Order of a vertex p. 21
Partial order p. 12
Partition (in the sense of the theory of sets) p. 3
Path,  , simple, composite, elementary, length p. 7 , simple, composite, elementary, length p. 7
Path, Hamiltonian p. 107
Peripheral point p. 119
Piece p. 201
Product, Cartesian 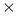 p. 2 p. 2
Product, of graphs p. 23
RADIUS p. 120
Roeette p. 123
Semi-factor p. 187
Set p. 1
Set, externally stable p. 40
Set, internally stable p. 35
Shrinkage p. 123
Sink p. 71
Source p. 71
Strategy p. 60
Strategy, mixed p. 228
Subgame p. 68
Subgraph p. 6
Subgraph, partial p. 6
Sum, digital p. 24
Sum, logical p. 42
Sum, of graphs p. 23
Support, isolated, pendant p. 162
Support, of a simple graph p. 90
Support, of any graph p. 184
Track p. 126
TRANSFER p. 89
TREE p. 162
union p. 2
Vertex p. 6
Weak ordering p. 11
Weak ordering, total p. 12
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



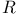 , space of real numbers
, space of real numbers  , simple, composite
, simple, composite 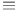
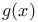



 -chromatic
-chromatic 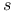 -graph
-graph  -finite,
-finite,  -finite,
-finite, 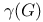
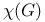 , connection
, connection