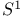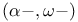|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Bartsch T. — Topological Methods for Variational Problems with Symmetries |
|
|
 |
| Предметный указатель |
 -category 12 31f -category 12 31f
 -category, properties 15—17 19 -category, properties 15—17 19
 -genus 12f 31f -genus 12f 31f
 -genus, properties 17—19 -genus, properties 17—19
Admissible representations 24 34 48
Antisymplectic matrix 128
Attractor 87
Attractor-repeller pair 87
B-index 13f
bg 56
Borel cohomology 55f 82
Borel stable cohomotopy 80
Borsuk — Ulam function 49f
Borsuk — Ulam theorem 33 52 75
Brake orbit 138f
Burnside ring 39 81 83
Category, equivariant 12
Center manifold theorem 109f
Classifying space 56
CN-group 37
Coefficient ring 54
Cohomological index 61f
Compact equivariant category 23
Conjugacy class 9
Conley index 88
Connecting orbit 87 91 120 123
Connection matrix 93
Continuation 88 94 99
Continuity property of A-category 15
Continuity property of A-genus 18
Continuity property of cohomology theory 54f
Continuity property of exit-length 99
Continuity property of length 63
Continuous cohomology theory 54
Cup-length 57
Cup-product 54
Cyclic group 46f 50 76f
Deformation monotonicity 15
Degree function 36
Dirichlet problem 27f
EG 55
eigenvalue problems 21 23f
Entry length 97
Equivariant cohomology theory 54 (see also Borel cohomology)
Equivariant cohomology theory, K-theory 77
Equivariant cohomology theory, stable cohomotopy 80 83
Equivariant cup-length 58
Euler class 74 79
Excision property of the length 63
Exit length 97—99
Exit length, properties 99 101f
Exit set 88
Fixed point set 9
Flow 87
Flow, gradient-like 87
Flow, parametrized 88
Frobeiiius group 37
G-jargon, ANR 11
G-jargon, Banach space 10
G-jargon, CW-complex 10
G-jargon, Hilbert space 10
G-jargon, map 9
G-jargon, Morse decomposition 87
G-jargon, orbit 9
G-jargon, space 9
G-jargon, vector space, normed 10
Generalized symplectic matrix 128
Genus 12f
Genus, properties 17—19
Geometrical index 14
Gradient-like flow 87
Grassmann manifold 56
Groups, 3-step group 37
Groups, CN-group 37
Groups, cyclic group 46f 50 76f
Groups, Frobenius group 37
Groups, O(3) 114—117
Groups, p-group 31 48—50 80
Groups, p-toral group 31 33f
Groups, p-torus 22 73
Groups, semisimple Lie group 32f
Groups, simple group 32f
Groups, SO(3) 47 114
Groups, torus 22 73
Gysin sequence 74
Hamiltonian system 128
Homogeneous G-space 9
| Hopf bifurcation 141
Hyperbolic 93f
Index pair 88
Induced representation 35
Intersection property of the length 63
Invariant sphere theorem 111
Invariant subset 87
Isolated invariant set 87
Isolating neighborhood 87
Isotropy group 9
Join 12
K-theory, equivariant 77
Lattice of isotropy subgroups 116
Length 59
Length for 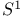 60 60
Length for 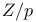 60f 67 60f 67
Length, properties 63—65 68
Limit sets 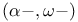 87 87
Lyapunov function 87
Maximal invariant subset 87
Monotonicity property of  -genus 17 -genus 17
Monotonicity property of length 63
Morse decomposition 87
Mountain Pass Theorem 21
Multiplicative cohomology theory 54
Noetherian module 63
Noetherian ring 57
Normal mode solution 139f
Normalization property of  -category 15 -category 15
Normalization property of  -genus 17 -genus 17
Normalization property of length 63 68
Normed G-vector space 10
Orbit 9
Orbit space 9
Orthogonal group O(3), lattice of isotropy subgroups 116
Orthogonal group O(3), representations 115
Orthogonal group O(3), subgroups 114f
p-group 31 48—50 80
p-toral group 31 33f
p-toral Sylow subgroup 32
p-torus 22 73
Palais — Smale condition 20
Parametrized flow 90f
Piercing property of length 65
Positively invariant 88
Principles of symmetry reduction 31
Product flow 88
Properties of  -category 15—17 19 -category 15—17 19
Properties of  -genus 17—19 -genus 17—19
Properties of cohomology theories 54
Properties of length 63—65 68
Regular index pair 88
Related by continuation 89
Repeller 87
Representation of O(3) 115
Representation of SO(3) 47
Representation, admissible 24 34 48
Representation, induced 35
Segal conjecture 81
Semisimple Lie group 32f
Set valued genus 14
Signature 134
Simple group 32f
Space of conjugacy classes 9f 35
Special orthogonal group SO(3), irreducible representations 47
Special orthogonal group SO(3), subgroups 47 114
Spherical harmonics 47 115
Stable cohomotopy theory 80 83
Stable set 97
Stiefel manifold 56
Strong normalization property 68
Subadditivity property of  -category 15 -category 15
Subadditivity property of  -genus 18 -genus 18
Subadditivity property of length 63
Subconjugate 10
Submaximal isotropy group 118
Symmetry breaking 118
Symplectic matrix 128
Telescope 42f
Tietze — Gleason theorem 10
Torus group 22 73
Triangle inequality for length 63
Unstable set 97
Weak monotonicity property 19
Weinstein — Moser theorem 129 138f
Weyl group 9
Whitehead theorem 11
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -category
-category