Авторизация
Поиск по указателям
do Carmo M.P. — Riemannian geometry
Обсудите книгу на научном форуме Нашли опечатку?
Название: Riemannian geometryАвтор: do Carmo M.P. Аннотация: This text has been adopted at: University of Pennsylvania, Philadelphia University of Connecticut, Storrs Duke University, Durham, NC California Institute of Technology, Pasadena University of Washington, Seattle Swarthmore College, Swarthmore, PA University of Chicago, IL University of Michigan, Ann Arbor "In the reviewer's opinion, this is a superb book which makes learning a real pleasure." ¿ Revue Romaine de Mathematiques Pures et Appliquees "This main-stream presentation of differential geometry serves well for a course on Riemannian geometry, and it is complemented by many annotated exercises." ¿ Monatshefte F. Mathematik "This is one of the best (if even not just the best) book for those who want to get a good, smooth and quick, but yet thorough introduction to modern Riemannian geometry." ¿ Publicationes Mathematicae Contents: Differential Manifolds * Riemannian Metrics * Affine Connections; Riemannian Connections * Geodesics; Convex Neighborhoods * Curvature * Jacobi Fields * Isometric Immersions * Complete Manifolds; Hopf-Rinow and Hadamard Theorems * Spaces of Constant Curvature * Variations of Energy * The Rauch Comparison Theorem * The Morse Index Theorem * The Fundamental Group of Manifolds of Negative Curvature * The Sphere Theorem * Index Series: Mathematics: Theory and Applications
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1992Количество страниц: 300Добавлена в каталог: 14.09.2005Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Action of a group 22 164 Action of a group, discontinuous 23 165 Action of a group, free 165 Action of a group, transitive 165 Axiom, countable basis 30 Axiom, Hausdorff 30 Axiom, of free mobility 167 Bianchi identities 91 106 Bundle, normal 134 Bundle, tangent 15 Bundle, tangent, metric in the 79 (Ex.) Bundle, tangent, parametrization of the 15 Christoffel symbols 55 58 Clairaut's relation 78 Clifford torus 140 (Ex.) Coefficient of conformality 169 Conformal metrics 160 181 Conformal metrics, connections of 181 (Ex.) Connection, affine 50 Connection, compatible with the metric 53 Connection, Levi — Civita 55 Connection, normal 134 Connection, of a Riemannian submersion 186 (Ex.) Connection, pseudo-Riemannian 59 (Ex.) Connection, Riemannian 55 Connection, symmetric 54 Contractible subset 81 (Ex.) Covariant derivative 50 Curvature constant 96 Curvature Gauss — Kronecker 129 Curvature mean 129 142 Curvature mean, curvature vector 133 Curvature normal 135 Curvature of a Riemannian submersion 187 (Ex.) Curvature of horospheres and hyperspheres 184 (Ex.) Curvature of the complex projective space 188 (Ex.) Curvature of the hyperbolic space 162 Curvature of the sphere 131 Curvature principal 129 Curvature principal, of a Riemannian manifold 89 Curvature Ricci 97 Curvature scalar 97 Curvature scalar, as an integral 107 (Ex.) Curvature sectional 94 131 162 Curvature sectional, constant sectional 96 Curvature sectional, geometric interpretation of 132 Curve, differentiable 6 Curve, divergent 153 (Ex.) Curve, parametrized 42 Curve, piecewise differentiable 67 Cut locus 267 Diffeomorphism 10 Diffeomorphism, local 10 Differentiable structure 2 Distance 146 Divergence 83 (Ex.) Divergence, as variation of volume 86 (Ex.) Divergence, mean curvature as a 142 (Ex.) Embedding 11 32 Energy 194 Equation, Codazzi 137 Equation, Gauss 130 135 Equation, Jacobi 111 Equation, Killing 82 (Ex.) Equation, Ricci 135 Fields, Jacobi 111 Fields, Jacobi, on spaces of constant curvature 112 Fields, Jacobi, on symmetric spaces 121 (Ex.) Fields, Killing 81 (Ex.) Fields, Killing, singularities of a 82 (Ex.) 104 123 143 Fields, left invariant vector 40 Fields, parallel vector 52 Fields, variational 192 First fundamental form 35 Flat torus 42 46 Flat torus, as a minimal submanifold of 140 (Ex.) Flow of a vector field 28 63 Focal sot 232 Formula, for the first variation 195 Formula, for the second variation 198 Free homotopy class 254 Geodesic 61 Geodesic flow 63 Geodesic frame 83 (Ex.) Geodesic ray 153 (Ex.) Geodesic segment 61 Geodesic sphere 70 Geodesic triangle 258 Geodesic, closed 254 Geodesic, in a Riemannian manifold 153 Geodesic, in a Riemannian manifold, ray starting from 153 Geodesic, in a surface of revolution 77 (Ex.) Geodesic, in the hyperbolic space 162 Geodesic, in the sphere 66 Geodesic, lasso 254 Geodesic, minimizing 67 Geodesic, normalized 61 Geodesic, radial 70 Geodesic, translation along a 257 Geometry, elliptic 168 Geometry, hyperbolic 168 Geometry, non-Euclidean 167 Geometry, spherical 168 Gradient 83 (Ex.) hessian 141 (Ex.) 277 Homogeneous space 154 (Ex.) Horosphere 178 Hyperbolic plane 46 (Ex.) Hyperbolic plane, completeness of 153 (Ex.) Hyperbolic plane, connection of 58 (Ex.) Hyperbolic plane, geodesics of 73 Hypersphere 178 Hypersurface 129 Immersion 11 Immersion, applications of Index Lemma to 221 Immersion, codimension of a 11 Immersion, isometric 39 Immersion, J.D. Moore Theorem 221 Immersion, minimal 133 Immersion, totally geodesic 132 Immersion, totally geodesic, in a Lie group 140 (Ex.) Immersion, umbilic 182 Index form 242 Index of a quadratic form 243 Index of a quadratic form, of a critical point 277 Infinitesimal isometry see “Killing field” Injectivity radius 271 Interior product 84 (Ex.) inversion 169 Isometry 38 Isometry, infinitesimal 81 (Ex.) Isometry, local 39 Jacobi identity 27 Klein bottle 25 Klein bottle, embedding in 33 (Ex.) Klein bottle, nonorientability of 33 (Ex.) Laplacian 83 (Ex.) 143 Lemma, Index 212 Lemma, Index, for focal points 234 Lemma, Klingenberg 236 (Ex.) Lemma, of Berger 282 Lemma, of Gauss 69 Lemma, Otsuki 225 Lie group 39 Lie group, connection of a 103 (Ex.) Lie group, curvature of a 103 (Ex.) Lie group, geodesies of a 80 (Ex.) Lie group, Lie algebra of a 40 Lie group, one-parameter subgroup 80 (Ex.) Line 252 (Ex.) Lobatchevski plane see “Hyperbolic plane” Locus, conjugate 117 Locus, cut 267 Manifold, complete 145 Manifold, differentiable 2 Manifold, Einstein 108 (Ex.) Manifold, extendible 145 Manifold, focal point free 233 Manifold, homogeneous 154 (Ex.) Manifold, orientable 18 Manifold, oriented 18 Manifold, product 32 Manifold, Riemannian 38 Map, conformal 168 Map, differentiable 5 Map, differential of a 10 Map, exponential 65 Map, Gauss spherical 129 Map, orientation preserving 18 Metric, bi-invariant 40 Metric, bi-invariant, on a compact Lie group 46 (Ex.) Metric, covering 152 (Ex.) Metric, flat torus 42 Metric, induced by a covering 165 Metric, induced by an immersion 39 Metric, left invariant 40 Metric, Lorentzian 59 (Ex.) Metric, non-euclidean of Lobachevski 46 (Ex.) Metric, product 42 Metric, pseudo-Riemannian 58 (Ex.) Metric, Riemannian 38 79 Mobius band 25 33 Mobius band, infinite 33 (Ex.) Mobius band, nonorientability of 32 (Ex.) Multiplicity of a conjugate point 116 Neighborhood, convex 76 Neighborhood, coordinate 2 Neighborhood, normal 70 Neighborhood, normal, strongly 74 Neighborhood, totally normal 72 Normal ball 70 Normal coordinates 86 (Ex.) Nullity of a quadratic form 243 Orientable double covering 34 (Ex.) Orientation 18 Parallel transport 52 Parametrization 2 Parametrization, associated basis to a 9 Parametrized surface 67 Partition of unity 30 Point, conjugate 116 Point, conjugate, multiplicity 116 Point, critical 17 277 Point, cut 267 Point, focal 230 Polar coordinates 122 (Ex.) Pole 151 154 Principal directions 129 Projective plane, embedding in 32 (Ex.) Projective plane, nonorientability of 32 (Ex.) Regular surface 16 Relation of Clairaut 78 (Ex.) Second fundamental form 128 Space forms 164 Space, ball model 177 Space, complex projective 187 (Ex.) Space, complex projective, curvature of 188 Space, constant curvature of 156 Space, Euclidean 39 Space, hyperbolic 160 Space, hyperbolic, completeness of the 162 Space, hyperbolic, isometries of the 175 Space, hyperbolic, models of 160 177 180 Space, lens 181 Space, real projective 4 Space, real projective, metric on 45 Space, real projective, parametrizations of 4 20 Space, symmetric (locally) 105 (Ex.) Space, symmetric (locally), geometric characterization of 190 (Ex.) Space, symmetric (locally), Jacobi Melds on a 121 (Ex.) Space, tangent 9 Sphere theorem 265 Stereographic projection 19 Stereographic projection, of hyperbolic space 184 (Ex.) Strongly convex 74 Submanifold 11 see Submanifold, minimal 133 Submanifold, totally geodesic 132 Submanifold, umbilic 182 (Ex.) Submanifold, umbilic, in euclidean space 184 (Ex.) Submanifold, umbilic, in hyperbolic space 184 (Ex.) Submersion 185 (Ex.) Submersion, connection of a 186 Submersion, curvature of a 187 Submersion, horizontal vector of a 186 (Ex.) Submersion, Riemannian 185 (Ex.) Submersion, vertical vector of a 185 (Ex.) Support of a function 30 System of coordinates 2 Tangent vector 7 Tangent vector, to a curve 6 Tensor 100 Tensor, covariant derivative of a 102 Tensor, curvature 101 Tensor, metric 101 103 Tensor, metric, on a Riemannian manifold 100 Tensor, Ricci 98 Theorem, Morse Index 243 Theorem, of Bonnet — Myers 201 208 250 Theorem, of Cartan, on closed geodesies 255 Theorem, of Cartan, on determination of the metric 157 Theorem, of E. Hopf 85 (Ex.) Theorem, of Gauss 130 Theorem, of Hadamard 149 237 Theorem, of Hopf and Rinow 146 Theorem, of Jacobi 248 Theorem, of Liouville, on conformal transformations 170 Theorem, of Liouville, on the geodesic flow 86 (Ex.) Theorem, of Preissman 260 Theorem, of Rauch 215 Theorem, of Rauch, on focal points 234 Theorem, of Schur 106 (Ex.) Theorem, of Sturm 238 (Ex.) 240 Theorem, of Synge 206 Theorem, of Synge — Weinstein 203 Theorem, sphere 265 Trajectory of a vector field 28 Value, critical 17 Value, regular 17 Variation 192 Variation, proper 192 Vector field 25 Vector field, along a curve 43 Vector field, along a surface 68 Vector field, as a derivation 28 Vector field, bracket of 27 Vector field, horizontal lift of a 186 (Ex.) Vector field, trajectory 28 Vertex of a curve 67 Volume, element 45 84 86 Volume, form 45 Volume, in a Riemannian manifold 44
Реклама
 |
|
О проекте
|
|
О проекте



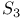
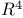 of
of