Авторизация
Поиск по указателям
Bóna M. — A Walk Through Combinatorics: An Introduction to Enumeration and Graph Theory
Обсудите книгу на научном форуме Нашли опечатку?
Название: A Walk Through Combinatorics: An Introduction to Enumeration and Graph TheoryАвтор: Bóna M. Аннотация: This is a textbook for an introductory combinatorics course that can take up one or two semesters. An extensive list of problems, ranging from routine exercises to research questions, is included. In each section, there are also exercises that contain material not explicitly discussed in the preceding text, so as to provide instructors with extra choices if they want to shift the emphasis of their course. Just as with the first edition, the new edition walks the reader through the classic parts of combinatorial enumeration and graph theory, while also discussing some recent progress in the area: on the one hand, providing material that will help students learn the basic techniques, and on the other hand, showing that some questions at the forefront of research are comprehensible and accessible for the talented and hard-working undergraduate. The basic topics discussed are: the twelvefold way, cycles in permutations, the formula of inclusion and exclusion, the notion of graphs and trees, matchings and Eulerian and Hamiltonian cycles. The selected advanced topics are: Ramsey theory, pattern avoidance, the probabilistic method, partially ordered sets, and algorithms and complexity. As the goal of the book is to encourage students to learn more combinatorics, every effort has been made to provide them with a not only useful, but also enjoyable and engaging reading.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Издание: Second EditionГод издания: 2006Количество страниц: 481Добавлена в каталог: 24.04.2010Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
454 376 117 445 450 38 94 94 448 449 448 122 454 452 23 44 452 452 437 189 446 450 436 138 Acyclic function 226 Adjacency matrix 218 Anti-automorphism 395 Antichain 378 ascent 325 atom 398 Augmenting path 253 Automorphism 196 Bayes’ Theorem 354 356 Bell numbers 93 Bijection 41 Binet — Cauchy formula 221 Binomial coefficients 44 Binomial coefficients, for a real exponent 73 Binomial theorem 65 Binomial theorem, for a real exponent 73 Bipartite graphs 243 Bipartite graphs, complete 200 213 245 Boolean algebra 376 Boolean expression 447 BREADTH FIRST SEARCH 425 Brooks theorem 256 Bubblesort 409 Canonical cycle form 111 Catalan numbers 179 311 Cayley’s formula 211 Center of a graph 228 Chain 376 Chain cover 379 Chain, length of 382 Chromatic number 242 Chromatic polynomial 259 260 CLIQUE 288 Coatom 398 Complement in a lattice 395 Complement of a graph 228 Complement of a permutation 126 312 Complement of a set 44 Complete graph 191 Complete graph, 254 Composition of an integer 89 Composition of an integer, weak composition 89 Compositional formula for exponential gen. functions 166 Compositional formula for ordinary gen. functions 159 Conjunctive normal form 447 Connected components 185 Connected graph 185 Connected graph, strongly 191 CONp 440 Cook’s theorem 448 Covering matrix 395 Covering relation 371 cube 277 Cycles in graphs 188 Cycles in permutations 110 Decreasing binary tree 323 Degree of a vertex 184 Depth first search 425 Derangements 135 Descent 138 325 Diameter of a graph 232 Dijkstra algorithm 421 Dilworth’s theorem 379 Dimension of a poset 395 Direct product of posets 382 Directed graph 190 Distance in a graph 228 Distribution problems 89 Distributive lattice 395 dodecahedron 278 Dominance order 398 Dual of a planar graph 276 Durfee-square 101 Edge-cover 262 Erd 294 Eulerian walk 185 Eulerian walk, closed 185 Euler’s theorem on planar graphs 270 Event 346 Excedance 138 Expectation 355 Expectation, conditional 361 Expectation, linearity of 357 Exponential formula 165 Exponential formula, permutation version 170 Factor-critical 261 Factorial 38 Ferrers shape 95 Fibonacci number 173 Fixed point 110 122 Fixed point, fixed point-free 134 Forest 210 Forest, rooted 213 Formal power series 147 Four-color theorem 281 Gap position 119 Generating function, composition of 157 164 Generating function, exponential 160 Generating function, ordinary 146 Generating function, products of 152 162 Graph 184 Graph, bipartite 243 Graph, connected 185 Graph, directed 190 Graph, minimally connected 207 Graph, planar 270 Graph, regular 197 Graph, simple 185 Graphical partition 198 Greedy algorithm 214 Hall’s theorem 251 Halting problem 408 Hamiltonian cycle 188 439 Hamiltonian path 188 Hasse diagram 377 Hypercube 200 icosahedron 278 Ideal 375 Ideal, principal 375 Immermann — Szelepcs 452 In-degree 191 In-order 324 Incidence algebra 381 Incidency matrix 221 Inclusion-Exclusion Principle 138 Incomparable elements 376 Indecomposable permutation 169 INDEPENDENT - SET$ 454 Independent events 351 355 Independent set of edges 248 Indicator variable 359 Induced subgraph 196 Induction, strong 24 Induction, weak 19 Injection 41 Input 408 Interval order 398 Interval order, unit 398 Inverse of a permutation 121 inversion 123 Involution 121 Isomorphism of graphs 194 Join 389 K 262 Kruskal algorithm 217 417 Kuratowski’s Theorem 272 Laplacian 224 Lattice 388 Leaf 210 Left-to-right maximum 126 Left-to-right minimum 313 Linear extension 380 Literal 447 Locally finite poset 381 Log-concave sequence 76 Lonely permutation 327 Loop 185 M 383 M 387 M 383 Magic square 50 260 Matching 250 Matching, maximum, maximal 252 Matching, perfect 248 Matrix-tree theorem 222 Matrix-tree theorem, eigenvalue version 224 Maximum and maximal elements 377 Meet 389 Meet-semilattice 390 Mergesort 412 Modular lattice 395 Motzkin numbers 168 Multinomial coefficients 71 Multinomial theorem 70 72 Multiset 23 39 Mutually exclusive events 347 Nonconstructive proofs 348 Noncrossing partitions 330 Northeastern lattice paths 76 Octahedrite 282 octahedron 278 ODD( 117 One-line notation 111 Order polynomial 397 Ordered degree-sequence 198 Out-degree 191 Output 408 Parking function 226 Partial fraction decomposition 148 Partially ordered set 375 Partitions of a set 91 Partitions of a set, formula for the number of 136 Partitions of a set, noncrossing 325 Partitions of a set, type of 98 Partitions of an integer 94 Partitions of an integer, asymptotic formula 95 Partitions of an integer, conjugate 95 Partitions of an integer, self-conjugate 95 Pascal triangle 67 Path 185 Pattern avoidance 307 Peak 362 permutations 37 Permutations, alternating 169 Permutations, even 122 Permutations, indecomposable 169 Permutations, matrix of 121 Permutations, odd 122 Permutations, of a multiset 40 Permutations, roots of 122 Permutations, stack sortable 319 Permutations, two-stack sortable 321 Permutations, type of 113 Permutations, with restricted cycles 116 Petersen graph 198 Pigeon-hole principle 1 3 Polyhedron 272 Polyhedron, trivalent 282 POSET 370 Postorder 324 Pr 226 Pratt’s theorem 441 PRIMES$ 440 Prim’s algorithm 431 probability 345 Probability, conditional 351 Product formula for ex 163 Product formula for ord. gen. functions 152 Ramsey number 290 Ramsey theorem 289 Random variable 356 Random variable, independent 357 Reachability 452 Refinement order 377 Refining sequence 227 Reflection principle 85 Regular polyhedra 269 Right-to-left maximum 314 Rooted forest 210 Roots of a permutation 121 Run 362 Sample space 346 Saturated non-factorizable 257 Schr 169 Self-dual poset 395 Semi-factorial 73 Set 22 Sieve formula 132 Simpson’s paradox 353 Spanning tree 214 Spanning tree, minimum weight 217 Sperner’s lemma 283 Stack-sorting 319 Standard deviation 365 Stanley — Wilf conjecture 311 Stirling numbers of the first kind 113 Stirling numbers of the second kind 91 Stirling’s formula 38 Strings over a finite alphabet, with no repetitions allowed 43 Strings over a finite alphabet, with repetitions allowed 40 Subgraph 196 Subgraph, induced 196 SUBSETSUM$ 450 Superpattern 332 Surjection 41 Surjection, number of 92 Symmetric difference 208 Symmetric group 112 tetrahedron 277 Three houses, three wells 270 Tournament 191 Tournament, transitive 192 Trace 127 Transition lemma 115 TREE 209 Tree, complete 226 Tree, decreasing binary 323
Реклама
 |
|
О проекте
|
|
О проекте




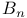
 (
(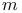 )
) 

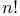
 (
( )
) 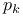 (
(
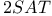

 (
(

![$[N]$](/math_tex/9c311325428306b413fc16c6f6ea901582.gif)
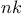


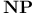

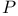
 (
( -partite
-partite  s — Szekeres theorem
s — Szekeres theorem  nyi theorem
nyi theorem  fer code
fer code