|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Boothby W.M. — An Introduction to Differentiable Manifolds and Riemannian Geometry |
|
|
 |
| Предметный указатель |
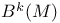 , exact forms 274 , exact forms 274
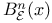 , , 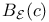 , open ball of , open ball of  2 2
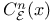 , , 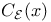 , open cube of , open cube of  2 2
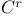 , ,  differentiability class 21—22 66 differentiability class 21—22 66
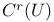 , , 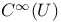 , , 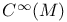 differentiable functions on U or M 22 107 differentiable functions on U or M 22 107
 function 22 66 function 22 66
 mapping 66 mapping 66
 -compatibility 52 -compatibility 52
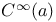 , , 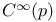 , germs of , germs of  -functions at a, p, etc. 32 107 -functions at a, p, etc. 32 107
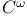 , real analytic functions 24 , real analytic functions 24
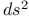 , metric tensor 188 , metric tensor 188
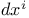 , coordinate coframes 182 , coordinate coframes 182
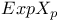 , exponential mapping 337 , exponential mapping 337
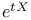 , one-parameter group of matrices 148 , one-parameter group of matrices 148
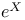 , exponential of a matrix 147 , exponential of a matrix 147
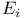 , , 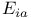 , , 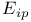 coordinate frames 30 110 118 coordinate frames 30 110 118
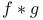 , product of paths 268—269 , product of paths 268—269
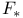 , F*, linear mappings induced by F 109 121 180 184 202 , F*, linear mappings induced by F 109 121 180 184 202
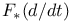 , tangent vector to curve 112 , tangent vector to curve 112
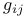 , coefficients of metric tensor 188 320 , coefficients of metric tensor 188 320
 , half-plane as hyperbolic space 167 361 409—412 , half-plane as hyperbolic space 167 361 409—412
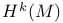 , H*(M), de Rham groups 274 , H*(M), de Rham groups 274
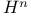 half space of half space of  11 252 11 252
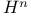 hyperbolic space 404 hyperbolic space 404
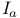 , inner automorphism 245 , inner automorphism 245
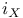 226 226
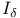 , , 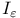 131 131
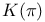 , sectional curvature 385 , sectional curvature 385
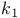 , , 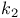 , principal curvatures to surface 370 , principal curvatures to surface 370
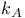 , characteristic function of A 231 , characteristic function of A 231
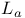 , , 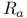 , , 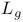 , left and right translations on Lie group 84 121 , left and right translations on Lie group 84 121
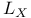 on on 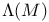 226 226
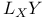 , Lie derivative of vector field 154 , Lie derivative of vector field 154
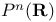 , real projective space 15 61 , real projective space 15 61
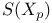 , shape operator 367—368 , shape operator 367—368
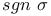 , sign of a permutation 203 , sign of a permutation 203
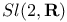 , acting on , acting on  361 361
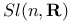 , special linear group 84 , special linear group 84
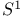 , ,  , ,  circle, 2—sphere, n-sphere 7 57 80 circle, 2—sphere, n-sphere 7 57 80
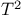 , , 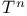 , torus 7 57 80 82 , torus 7 57 80 82
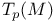 , , 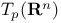 , tangent space at point 8 29 32 107—108 , tangent space at point 8 29 32 107—108
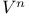 , vector space of n-tuples 2 , vector space of n-tuples 2
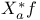 , directional derivative 32 , directional derivative 32
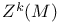 , closed forms 274 , closed forms 274
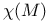 , Euler characteristic 14 415 , Euler characteristic 14 415
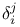 , Kronecker delta 179 , Kronecker delta 179
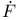 , tangent vector to curve 126 , tangent vector to curve 126
 , discrete group 97 , discrete group 97
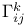 , , 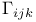 , Christoffel symbols 313 321—322 , Christoffel symbols 313 321—322
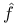 , f expressed in local coordinates 65 , f expressed in local coordinates 65
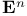 , Euclidean space 4 , Euclidean space 4
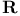 , real numbers 1 , real numbers 1
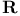 , real numbers as additive group 123 , real numbers as additive group 123
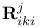 , , 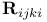 , coefficients of curvature tensor 327 384 , coefficients of curvature tensor 327 384
 , n-tuples of real numbers 1—3 , n-tuples of real numbers 1—3
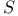 , symmetric group 166 203 215 , symmetric group 166 203 215
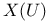 , , 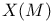 , ,  vector fields on U or M 40 122 151 vector fields on U or M 40 122 151
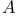 , alternating mapping 204 , alternating mapping 204
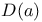 , , 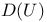 , algebra of derivations 33 40 108 , algebra of derivations 33 40 108
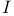 , homotopy operator on , homotopy operator on 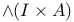 277 277
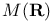 , , 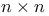 real matrices 56 59 real matrices 56 59
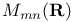 , , 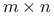 real matrices 27 56 59 real matrices 27 56 59
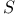 , symmetrizing mapping 204 , symmetrizing mapping 204
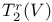 , , 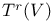 , , 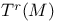 200 202 208 200 202 208
 , connection on a manifold 317 , connection on a manifold 317
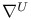 , restriction of a connection 319 , restriction of a connection 319
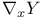 , covariant derivative 314—316 , covariant derivative 314—316
 , volume element 215—219 , volume element 215—219
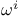 , , 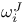 , connection forms 329 390—392 , connection forms 329 390—392
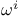 , coframes, dual basis 178 , coframes, dual basis 178
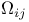 , curvature forms 390 , curvature forms 390
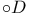 , interior of D 231 , interior of D 231
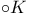 , interior of K 193 , interior of K 193
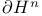 , , 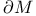 , boundary of , boundary of 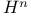 , M 253—254 , M 253—254
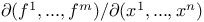 , Jacobian matrix 26 , Jacobian matrix 26
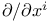 , natural frames of , natural frames of  36 36
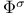 204 204
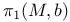 , fundamental group 270 , fundamental group 270
 —compact space 193 —compact space 193
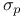 , involutive isometry 351 , involutive isometry 351
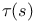 , torsion of space curve 303 , torsion of space curve 303
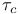 , translation along geodesic 354 , translation along geodesic 354
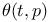 , , 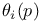 , , 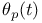 , action of , action of 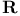 on on 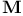 123 123
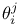 connection forms 328 connection forms 328
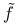 , , 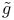 , lift of a mapping 289 , lift of a mapping 289
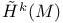 , invariant de Rham groups 285 , invariant de Rham groups 285
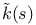 , curvature of plane curve 305 , curvature of plane curve 305
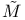 , covering manifold of M 101 289—295 , covering manifold of M 101 289—295
 , distribution 159 , distribution 159
(D/dt)(dp/dt) = 0, equation of geodesic 330—331
A', 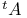 , transpose of matrix 85 150 184 357 , transpose of matrix 85 150 184 357
A*, transpose conjugate of complex matrix 357
Acceleration of moving particle 304
Action of group on manifold 90—96 123 165
Action of group on manifold, (properly) discontinuous 96
Action of group on manifold, effective 91
Action of group on manifold, free 94
Action of group on manifold, transitive 92—93 165—172
Ad g, adjoint homomorphism 245
Adjoint representation of Lie group 246
Admissible neighborhood of covering 101
Algebra of differential forms on M, 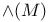 214 214
Almost continuous function 230
Alternating tensor 202
Antipodal map of 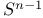 283 283
Approximation theorems 197 289
Approximation theorems, Weierstrass 197
Arc length 187—188
Arc length as parameter 301
Asymptotic direction on surface 374
Atlas 59
Automorphisms of Lie algebras 245
Automorphisms of Lie groups 245
Autonomous system of differential equations 131
Basis of covariant tensors 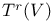 200—201 200—201
Basis of vector space 1—3
Basis, canonical (natural) 2
Basis, dual 177
Basis, oriented 215
Bilinear form 183—187
Bilinear form, induced mapping of 185
Bilinear form, skew symmetric 184
Bilinear form, symmetric, positive definite 184
Binormal to space curve 303
Brouwer fixed point theorem 282
Bundle see "Tangent bundle"
c(A), Jordan content of a set 230
C*, multiplicative group of complex numbers 82
Canonical basis of  2 2
Center of a Lie algebra 289 388
Chain rule 23
Chain rule for mappings 27
Change of variables in integration 233
Characteristic function of a set 231
Chart 59
Closed differential form 274
Coframes 179
Complete integrability 160
Complete vector field 142
Components of a bilinear form 184
Components of a covector 179
Connected sum of manifolds 258
Connection 317—323
Connection forms 328 390
Connection, restriction of 319
Connection, Riemannian 318
Constant curvature, manifold of 386 406—413
Constant vector field 323
Content zero in  230 230
Content zero on a manifold 235
| Contractible space 270
Contracting mapping theorem 43
Coordinate coframes 179
Coordinate frames 110
Coordinate function 52
Coordinate neighborhoods 52—56
Coordinate neighborhoods open balls and cubes 55
Coordinates, local 10
Coordinates, oriented 215
Coset space 94
Coset space, group action on 165
Covariant derivative see "Differentiation of vector fields"
Covariant tensor field 201—205
Covariant tensor field, induced mapping of 202
Covector, field 178
Covector, tangent 178—179
Covering manifolds 101 289—296
Covering manifolds, isomorphism of 293
Covering map 101
Covering transformation 101
Covering, locally finite 11 193
Covering, refinement of 11 193
Covering, regular, by spherical (cubical) neighborhoods 194
Cube, on a manifold 237
Curvature of plane curve 305
Curvature of space curve 302
Curvature of surface 18 374
Curvature, Riemannian 325—327
Curvature, Riemannian forms 389
Curvature, Riemannian sectional curvature 385 393
Curvature, Riemannian symmetries of 383
Curve differentiable 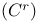 22 22
Cutting and pasting of manifolds 11—14 258
d(p, q) metric on Riemannian manifold 189
d, 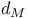 , exterior derivative 220 , exterior derivative 220
de Rham group 274
de Rham's theorem 275
Deck transformation 101
Dependent functions 50
Derivation(s) into 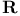 33 33
Derivation(s) on 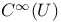 39 39
Derivative of vector field 314
Derivative, exterior 220—227
Derivative, exterior properties of 220
DF, DF(x), Jacobian matrix 27
df, differential of function 180
Diffeomorphism 67
Diffeomorphism on open sets of  41 41
Differentiable functions in weak sense 21
Differentiable functions on Euclidean space 21—25
Differentiable functions on manifolds 65—66
Differentiable manifold see "Manifolds"
Differentiable mapping, weak sense 26 67
Differentiable mappings composition of 28 67
Differentiable mappings on Euclidean space 25—28
Differentiable mappings on manifolds 65—67
Differentiable structure 53
Differentiable submanifold see "Submanifold"
Differential equations, existence theorem, proof 174
Differential equations, systems of 131—137
Differential forms 213
Differential forms, closed 226 274
Differential forms, exact 226 274
Differential forms, exterior 213
Differential of function 180
Differential of mapping 109
Differentiation of vector fields along curves in  298 298
Differentiation of vector fields covariant differentiation 309 314—316
Differentiation of vector fields Lie derivative 154
Differentiation of vector fields on submanifolds of  307—316 307—316
Directional derivative as tangent vector 32
Discrete group, action of 96—100
Distribution, involutive 159—224
Distribution, local basis of 159
Distribution, on a manifold 159
Divergence theorem 262
Domain of integration in  230 230
Domain of integration on a manifold 235
Double of manifold with boundary 255
dp/dt, tangent vector to curve p(t) 126
Dual basis 177
Dual vector space 177
DX/dt, DY/dt, covariant derivative 309
Dynamics of moving particle 304
dZ/dt, derivative of vector field 300
E, F, G coefficients of first fundamental form 242 373
Effective action of a group 91
Einstein manifold 387
Equations of structure 391
Equivalence relation, open 60
Euclidean space 4—6
Euclidean vector space 2
Euler characteristic 14 415
Euler's formula for surfaces 371
Exact differential form 274
Exponential mapping on Lie groups 150
Exponential mapping on Riemannian manifolds 337
Exponential of matrix 147
Exterior algebra 211
Exterior algebra of V, 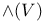 211 211
Exterior algebra, induced mapping of 213
Exterior differential form 213
Exterior differentiation 219—223
F(k, n), k-frames in 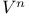 63 63
Fixed point of group action 92
Fixed point of mapping 282
Flags, space of 172
Flat coordinate neighborhood 160
Flow 127
Foliation 164
Forms connection 328—329 390
Forms curvature 390
Forms exterior differential 213—214
Forms, bilinear 183—187
Frames, coordinate 118
Frames, field of 38
Frames, orthonormal 329
Frames, parallel 299 323
Frames, space of 93
Free action of group 94
Frenet — Serret formulas 303
Frobenius' Theorem 161 233—236
Fundamental forms of a surface 370
Fundamental group 269—270
G(k, n), Grassmann manifold of k-planes in  63 168 362 63 168 362
G/H, homogeneous space, coset space 94 165
Gauss — Bonnet theorem 415
Gaussian curvature 18 375
Genus (of surface) 14
Geodesic sphere 344
Geodesics 191 312 330—335
Geodesics as one-parameter subgroups 355
Geodesics, minimal 346
Germs of  functions in functions in  36 36
Germs of  functions on manifold 115 functions on manifold 115
Gl(n, 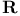 ), general linear group 56 ), general linear group 56
Grassman algebra see "Exterior algebra"
Grassman manifolds 63 168 362—363
Green's theorem 262
groups see "Action of group on manifold" "Discrete "Lie
G—invariance 124
H, mean curvature of surface 374—375
Homogeneous space 165—172
Homomorphism see "Lie group"
Homotopy 266—267
Homotopy of mapping 266
Homotopy of paths and loops 268
Homotopy operator 277
Homotopy, relative 267
Hopf — Rinow theorem 347
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



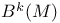 , exact forms
, exact forms 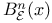 ,
, 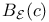 , open ball of
, open ball of 
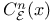 ,
, 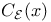 , open cube of
, open cube of 
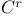 ,
,  differentiability class
differentiability class 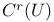 ,
, 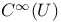 ,
, 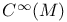 differentiable functions on U or M
differentiable functions on U or M 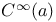 ,
, 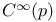 , germs of
, germs of 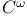 , real analytic functions
, real analytic functions 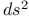 , metric tensor
, metric tensor 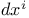 , coordinate coframes
, coordinate coframes 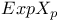 , exponential mapping
, exponential mapping 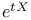 , one-parameter group of matrices
, one-parameter group of matrices 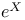 , exponential of a matrix
, exponential of a matrix 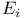 ,
, 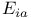 ,
, 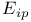 coordinate frames
coordinate frames 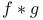 , product of paths
, product of paths 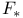 , F*, linear mappings induced by F
, F*, linear mappings induced by F 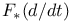 , tangent vector to curve
, tangent vector to curve 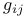 , coefficients of metric tensor
, coefficients of metric tensor  , half-plane as hyperbolic space
, half-plane as hyperbolic space 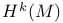 , H*(M), de Rham groups
, H*(M), de Rham groups 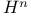 half space of
half space of 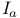 , inner automorphism
, inner automorphism 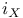
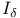 ,
, 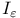
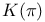 , sectional curvature
, sectional curvature 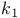 ,
, 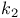 , principal curvatures to surface
, principal curvatures to surface 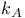 , characteristic function of A
, characteristic function of A 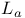 ,
, 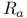 ,
, 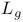 , left and right translations on Lie group
, left and right translations on Lie group 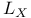 on
on 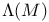
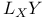 , Lie derivative of vector field
, Lie derivative of vector field 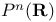 , real projective space
, real projective space 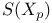 , shape operator
, shape operator 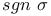 , sign of a permutation
, sign of a permutation 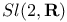 , acting on
, acting on 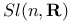 , special linear group
, special linear group 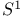 ,
,  ,
,  circle, 2—sphere, n-sphere
circle, 2—sphere, n-sphere 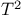 ,
, 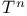 , torus
, torus 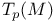 ,
, 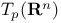 , tangent space at point
, tangent space at point 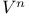 , vector space of n-tuples
, vector space of n-tuples 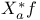 , directional derivative
, directional derivative 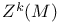 , closed forms
, closed forms 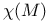 , Euler characteristic
, Euler characteristic 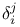 , Kronecker delta
, Kronecker delta 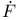 , tangent vector to curve
, tangent vector to curve  , discrete group
, discrete group 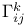 ,
, 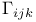 , Christoffel symbols
, Christoffel symbols 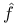 , f expressed in local coordinates
, f expressed in local coordinates 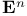 , Euclidean space
, Euclidean space 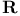 , real numbers
, real numbers 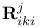 ,
, 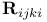 , coefficients of curvature tensor
, coefficients of curvature tensor 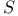 , symmetric group
, symmetric group 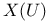 ,
, 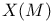 ,
, 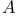 , alternating mapping
, alternating mapping 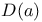 ,
, 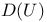 , algebra of derivations
, algebra of derivations 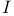 , homotopy operator on
, homotopy operator on 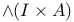
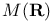 ,
, 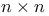 real matrices
real matrices 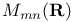 ,
, 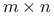 real matrices
real matrices 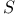 , symmetrizing mapping
, symmetrizing mapping 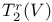 ,
, 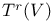 ,
, 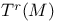
 , connection on a manifold
, connection on a manifold 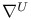 , restriction of a connection
, restriction of a connection 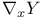 , covariant derivative
, covariant derivative  , volume element
, volume element 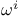 ,
, 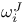 , connection forms
, connection forms 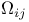 , curvature forms
, curvature forms 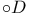 , interior of D
, interior of D 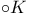 , interior of K
, interior of K 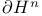 ,
, 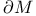 , boundary of
, boundary of 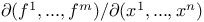 , Jacobian matrix
, Jacobian matrix 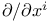 , natural frames of
, natural frames of 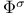
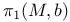 , fundamental group
, fundamental group  —compact space
—compact space 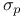 , involutive isometry
, involutive isometry 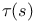 , torsion of space curve
, torsion of space curve 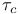 , translation along geodesic
, translation along geodesic 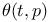 ,
, 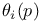 ,
, 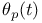 , action of
, action of 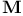
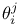 connection forms
connection forms 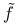 ,
, 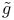 , lift of a mapping
, lift of a mapping 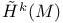 , invariant de Rham groups
, invariant de Rham groups 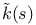 , curvature of plane curve
, curvature of plane curve 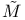 , covering manifold of M
, covering manifold of M  , distribution
, distribution 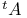 , transpose of matrix
, transpose of matrix 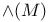
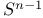
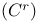
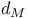 , exterior derivative
, exterior derivative