Авторизация
Поиск по указателям
Böttcher A., Grudsky S.M. — Spectral Properties of Banded Toeplitz Matrices
Обсудите книгу на научном форуме Нашли опечатку?
Название: Spectral Properties of Banded Toeplitz MatricesАвторы: Böttcher A., Grudsky S.M. Аннотация: This self-contained introduction to the behavior of several spectral characteristics of large Toeplitz band matrices is the first systematic presentation of a relatively large body of knowledge. Covering everything from classic results to the most recent developments, Spectral Properties of Banded Toeplitz Matrices is an important resource. The spectral characteristics include determinants, eigenvalues and eigenvectors, pseudospectra and pseudomodes, singular values, norms, and condition numbers. Toeplitz matrices emerge in many applications and the literature on them is immense. They remain an active field of research with many facets, and the material on banded ones until now has primarily been found in research papers. The book may serve both as a text for introducing the material and as a reference. The approach is based on the know-how and experience of the authors in combining functional analytical methods with hard analysis and in applying operator theoretical methods to matrix theory, which reveals the essence of several phenomena and leads to significant improvements in existing results. All basic results presented in the book are precisely stated as theorems and accompanied by full proofs. Audience This book is written for applied mathematicians, engineers, and scientists who encounter Toeplitz matrices in their research. It also will be of interest to mathematicians in the fields of operator theory, numerical analysis, structured matrices, or random matrix theory, and physicists, chemists, biologists, and economists who deal with stationary statistical and stochastic problems. Parts of the book are suitable for use as a graduate-level text on Toeplitz matrices or analysis.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 2005Количество страниц: 411Добавлена в каталог: 17.04.2010Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
211 250 261 219 60 33 347 43 335 347 43 6 179 3 11 347 355 178 28 90 11 3 79 313 223 46 61 377 49 61 377 181 96 9 347 157 157 157 341 313 31 165 219 2 64 6 4 90 315 328 313 313 313 315 315 137 262 262 262 complex numbers natural numbers real numbers 3 integers nonnegative integers 9 59 211 167 9 59 249 8 8 8 85 8 309 8 183 101 223 31 315 313 212 335 variance 211 225 211 59 122 101 96 5 90 60 225 249 12 60 Algebra 240 Algebra, 240 Algebra, Banach 240 Algebra, F 377 Algebra, irrational rotation 378 Algebra, Wiener 2 Algorithm, fast 77 Algorithm, superfast 77 Anderson model 374 Approximation number 211 Asymptotically extended sequence 302 Asymptotically good pseudoeigenvalue 300 Asymptotically good pseudomode 300 Asymptotically localized sequence 302 305 Avram — Parter theorem 219 Banach algebra 240 Banach algebra, unital 240 Banach — Steinhaus theorem 60 Baxter — Gohberg — Feldman theorem 63 Baxter — Schmidt formula 37 Bergman space 75 Beta distribution 233 Bounded variation 219 Branch point 264 367 Brown — Halmos theorem 102 Cauchy singular integral operator 75 Cauchy’s interlacing theorem 224 Chebyshev polynomial 22 CIRC 32 Circulant matrix 32 Cluster 224 Coker A 9 Cokernel 9 Componentwise condition number 332 Condition number 137 Condition number, componentwise 332 Condition number, for matrix inversion 328 Condition number, full structured 313 Condition number, normwise 313 Condition number, structured 313 Confluent Vandermonde 42 Convergence, critical behavior 177 Convergence, strong 59 Convergence, uniform 59 Convergence, weak 59 Critical transient phase 177 Determinant 46 Discrete Hamiltonian 335 Discrete Laplacian 335 Duduchava — Roch formula 92 Eigenvalue density 379 Essential spectrum 9 Exp 7 Expectation 225 Expected value 347 Exponentially decaying sequence 15 Extended sequence 17 F 377 Factorization, Wiener — Hopf 7 Fast algorithm 77 Fej 122 Field of values 167 Finite section method 64 Formula, Aaxter — Schmidt 37 Formula, Duduchava — Roch 92 Formula, Gohberg — Sementsul 77 Formula, Trench’s 41 Formula, Widom’s 38 65 Fourier coeffcients 2 Fourier matrix 32 Fredholm operator 9 Function of bounded variation 219 Galerkin method 74 Gauss — Seidel iteration 187 Gohberg — Sementsul formula 77 Hadamard’s inequality 80 Hamiltonian, discrete 335 Hankel matrix 2 Hardy space 11 Hardy’s inequality 91 Hatano — Nelson model 375 Higher order relative spectrum 175 Hilbert — Schmidt operator 45 Hirschman’s theorem 274 Homomorphism of 241 Hull, polynomial convex 208 Hull, polynomial numerical 179 Hurwitz’ theorem 355 Im A 9 Image 9 Ind A 9 INDEX 9 Inequality, Hadamard’s 80 Inequality, Hardy’s 91 Instability index 155 Interval matrix 256 Inverse closedness 240 Involution 240 Irrational rotation 378 Jacobi’s theorem 48 Ker A 9 Kernel 9 Krein — Rutman theorem 253 Kreiss matrix theorem 181 Laplacian, discrete 335 Laurent matrix 28 Laurent polynomial 8 Lim inf 163 Lim sup 163 Lin linear hull LOG natural logarithm Matrix, circulant 32 Matrix, finite Toeplitz 31 Matrix, Fourier 32 Matrix, infinite Hankel 2 Matrix, infinite Toeplitz 1 Matrix, Laurent 28 Matrix, monodromy group 367 Matrix, positive definite 101 Matrix, positive semi-definite 101 Matrix, Toeplitz-like 123 Matrix, tridiagonal Toeplitz 34 Norm surface 178 Normal solvability 9 Normwise condition number 313 Nowhere locally constant 364 Numerical range 167 Operator, Cauchy singular integral 75 Operator, Fredholm 9 Operator, Hilbert — Schmidt 45 Operator, normally solvable 9 Operator, trace class 45 Operator, Wiener — Hopf 74 Order of a zero 88 Polynomial convex hull 208 Polynomial numerical hull 179 Positive definite 101 Positive semi-definite 101 Preconditioning 259 Proper cluster 224 Pseudoeigenvalue 300 Pseudoeigenvalue, asymptotically good 300 Pseudomode 300 Pseudomode, asymptotically good 300 Pseudospectrum 157 Pseudospectrum, structured 157 Rad 12 Resolution of the identity 21 Resolvent 9 Riesz — Markov theorem 377 Schmidt — Spitzer theorem 274 Second order relative spectrum 175 Sequence, asymptotically extended 302 Sequence, asymptotically localized 302 305 Sequence, exponentially decaying 15 Sequence, extended 17 Sequence, stable 61 Singular value 211 Singular value decomposition 212 Singular value interlacing 216 Sky region 178 Sp 9 Space, Bergman 75 Space, Hardy 11 Spectral distribution 377 Spectral radius 12 Spectrum 9 Spectrum, absolutely continuous 21 Spectrum, essential 9 Spectrum, higher order relative 175 Spectrum, point 21 Spectrum, second order relative 175 Spectrum, singular continuous 21 Splitting phenomenon 212 Stable sequence 61 Stone’s formula 21 Strong convergence 59 Structured condition number 313 Structured condition number, for matrix inversion 328 Structured condition number, full 313 Structured pseudospectrum 157 Superfast algorithm 77 Symbol 3 Szeg 47 Szeg 44 Theorem, Avram — Parter 219 Theorem, Banach — Steinhaus 60 Theorem, Baxter — Gohberg — Feldman 63 Theorem, Brown — Halmos 102 Theorem, Cauchy’s interlacing 224 Theorem, Hirschman’s 274 Theorem, Hurwitz 355 Theorem, Jacobi’s 48 Theorem, Krein — Rutman 253 Theorem, Kreiss matrix 181 Theorem, Riesz — Markov 377 Theorem, Schmidt — Spitzer 274 Theorem, singular value interlacing 216 Theorem, Szeg 47 Theorem, Szeg 44 Theorem, Wiener’s 6 Toeplitz matrix 1 31 Toeplitz-like matrix 123 Tr 248 Trace 248 Trace class operator 45 Tracial state 377 Trench’s formula 41
Реклама
 |
|
О проекте
|
|
О проекте




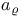
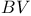 ,
, ![$BV[a, b]$](/math_tex/7a2cfdf3997617b0b55ddeeed22fbc1082.gif)

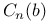
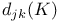
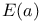

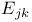

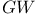 ,
, 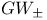
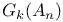
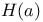

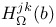
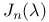
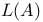


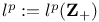
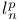
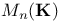

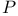 , probability
, probability 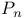
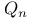
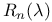
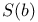
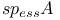
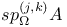
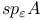
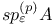
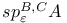
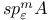
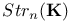
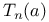
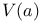
![$V_{[a,b]}f$](/math_tex/f88b5a7926eb738d6007236b90d36e8382.gif)
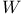
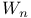
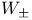
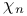
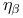
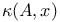
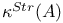
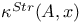
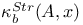

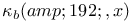
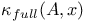
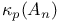
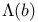
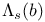

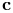

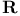
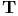 , complex unit circle
, complex unit circle 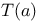
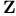
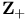
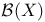
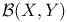
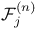
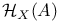 ,
,
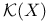
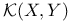
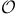

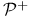
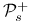 ,
, 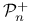
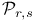
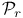
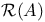
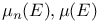
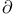 , boundary
, boundary 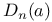

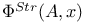
 ,
, 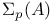
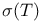
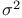
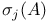
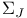
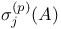
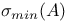
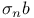

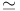
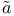

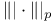
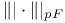


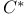
 lner
lner 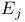
 r mean
r mean 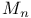
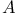
 — Widom limit theorem
— Widom limit theorem