|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Oden J.T. — Finite Elements: An Introduction (Vol. 1) |
|
|
 |
| Предметный указатель |
Shape functions, for quadrilaterals 196—197 207 236
Shape functions, for triangles 203—204 237
Shape functions, Lagrange families 62 72—74 195 204
Shape functions, master element 188—189
Shape functions, serendipity 196—197
Skew coordinates 200
Smoothness 10 see
Smoothness, of data 2 7 229 240 248
Smoothness, of solution 2 232 241
Smoothness, of test function 4 231 236 241
Sparseness 79
Specific heat 129 247
square-integrable 8 17—18 84 232
Stability, and time integration 250—252
State variable 44 48—49 246
State-dependent sources 50
Stiffness 33
Stiffness matrix 23 26 31 62 75 76 79—80 225 250
Stiffness matrix, banded 26
Stiffness matrix, element 24 see
Stiffness matrix, for Galerkin's method 12 59
Stiffness matrix, for two dimensions 164 187
Stiffness matrix, for two-point problems 81—86
Stiffness matrix, global 85
Stiffness matrix, sparseness of 24—26
Stiffness matrix, summability of 23 26
Stiffness matrix, symmetry 15 26
Stokes law 44
Strain energy 32 34
Strain energy, approximate 33
Strain-displacement relations 242
Stress 43 242—247
Stress, calculation of 127—130
String, on an elastic foundation 2 31
Subparametric map 193
Subspace, for Galerkin approximations 23 58
Subspace, of 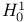 12 12
Superconvergence 36 124
Superparametric map 193—194
Symmetry, of stiffness matrix 15 26
Symmetry, of variational statement 5—10 14
System, differential 240—245 249—252
Taylor series 67
| Temperature 2 129 247
Tensor-product polynomials 159—160 195—196
Test function 6 7 9 14 16 54 58 230—232 248
tetrahedron 225—228
Thermal stress analysis 129
Three-dimensional problems 222—228
Time dependent problems 222 246—252
Transformation, of infinitesimals 178
Transformation, of shape functions 188—189
Transport terms 50
Trial functions 6 9 230—231
Triangle, curved 202
Triangle, discretization 109—111 149—150 199
Triangle, integration rules 205—208
Triangle, interpolation on 150—158 199—195
Triangle, map 200—201 204—205
Triangle, stiffness for linear element 169—174 207
Triangular coordinates see “Area coordinates”
Two-point problem, code for 87
Two-point problem, definition 41
Two-point problem, fourth-order 228—235
Two-point problem, physical origin of 42
Two-point problem, system 240—245
Two-point problem, variational statement of 52—58
Variational formulation, and minimization problem 60
Variational formulation, fourth-order problems 231 235
Variational formulation, systems 241
Variational formulation, three-dimensional problems 223—224
Variational formulation, time-dependent problems 249
Variational formulation, two-dimensional problems 162 165
Variational formulation, two-point problems 3—10 14 26 42 52—58 62 74
Vector field 133 222 240
Virtual work 244 246
Volume coordinates 228
Weak formulation 26
Weight function see “Test function”
Weighted average 144 248
Weighted-residual statement, fourth-order problem 229
Weighted-residual statement, system 240—241
Weighted-residual statement, time dependent problem 248—249
Weights of quadrature formula 93 190 192
Weights, definition of 93 199
Well-posed problems 56 240 see
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте