|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Beltrametti E.G., Cassinelli G. Ч The Logic of Quantum Mechanics (Encyclopedia of Mathematics and Its Applications - Vol 15) |
|
|
 |
| ѕредметный указатель |
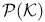 105Ч108 105Ч108
Atom of a lattice 98
Baer*-semigroups 178
Baer*-semigroups and orthomodular lattices 177Ч179
Baer*-semigroups, closed projections of 178
BellТs inequality 275
Boolean algebra 97
Boolean algebra, partied 267
Boolean algebra, sub algebra of poset 126
Borel sets 4
Center of lattice 128
Certainly-yes domain 142Ч143
Chain in a lattice 195
Chain in a lattice, f-closed subspaces 233
Closure relation 120 193 201
Closure relation, orthoclosure 202 212
Closure spaces 193
Closure spaces, closed subspaces of 193
Coherent subspaces 48Ч49
Commutativity in poset 125Ч128
Commuting self-adjoint operators 19
Complementarity 26 162Ч164
Composition conditions 258
Composition of physical systems 61Ч74 256Ч264
Conditional connective 222
Conditional connective, classical 222
Conditional connective, MittelstaedtТs. 224
Conditional connective, quantum 222Ч225
Conditioned probability with respect to Boolean algebra 285Ч287
Conditioned probability with respect to event 279Ч283
Conjunction 219Ч220
Continuous geometry 110
Convex set of states 6 209
Convex set of states, normed functioned on. 209
Convex set of states, polytope 211
Convex set of states, simplex 213
Convex set of states, strong polytope 213
Coordinatization, Hilbert-space 235Ч237
Coordinatization, vector-space 230Ч234
Coproduct of lattices 259
Correlation between subsystems 67Ч 72 81
Correlation between subsystems, coefficient of 68 273
Covering property 98 123 133 230
Cyclic vector 294
de MorganТs laws 96 221
Density operators 4
Direct product of lattices 131
Direct sum of lattices 131
Disjoint elements 97
Disjunction 220
Distributive triple 97
Dynamical group 53
Dynamical invariance 244
Dynamics 52Ч58 249Ч255
Dynamics of subsystems 72Ч73
Dynamics, Heisenberg picture 56Ч57 254
Dynamics, Markovian 54 250
Dynamics, reversible 54 251
Dynamics, Schroedinger equation 55Ч56
Dynamics, Schroedinger picture 53
Dynamics, stationary 54 250
Einstein, Podolsky, Rosen paradox 69Ч 72
Entropy of a state 287
Euclidean invariance 41Ч43
Evolution operator 53
Exclusion principle 65
Faces of convex set 210
Faces of convex set, detectable 211
Faces of convex set, orthoclosed 212
Faces of convex set, stable 213
FLATS 195Ч197
Free particle 37Ч41
Free particle,  101 101
GleasonТs theorem 115
GreechieТs examples 102
Hamiltonian of free particle 39 247
Hamiltonian operator 55Ч56 252Ч254
Heisenberg inequalities 24Ч26
Hermitian form 233
Hidden-variable theories 171 265
Hidden-variable theories, BellТs inequality 275
Hidden-variable theories, BellТs model of 268Ч270
Hidden-variable theories, contextual 172Ч174 175Ч176 271-276
Hidden-variable theories, Kochen and Specker model of 270Ч271
Hidden-variable theories, local 271Ч276
Hidden-variable theories, noncontextual 172Ч175 265Ч 271
Identical systems 63Ч65
Imprimitivity system 244
Induced representations 244
Information of state 287
Involution of field 233
Involutive ring 102
Involutive ring, projections of 103
Involutive semigroup 178
Involutive semigroup, projections of 178
Irreducibility 128 134
Isomorphism of orthomodular lattices 130
Join 96
Joint distributions 23 158
Lattices 97
Lattices, A. C. 95
Lattices, amalgamation 102
Lattices, atomic 98
Lattices, atomistic 98
Lattices, complete 97
Lattices, distributive 97
Lattices, implicative 224
Lattices, irreducible 128
Lattices, modular 98
Lattices, orthomodular 97
Lattices, separable 97
Logic of physical system 149 152
Measurement 79 181
Measurement ideal and of first kind 79 180Ч187
Measurement process 77Ч86
Measuring instrument 77Ч86
Meet 96
Mixtures 7 139
Mixtures, decomposition into pure states 7Ч12
Mixtures, ignorance interpretation of 11Ч12
Mixtures, nonunique decomposability 9Ч12 34Ч37
Modular geometric lattices 232
Modularity 98 107
Modus ponendo ponens 223
Momentum of free particle 38
Morphism of orthomodular lattices 130
Negation 220Ч221
Nonseparability 71
| Observables 153
Observables, associated with 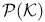 155 155
Observables, bounded 153
Observables, compatible 155
Observables, complementarity 162Ч164
Observables, complete set of compatible 157
Observables, function of 156Ч157
Observables, joint distribution of compatible 158
Observables, mean value 154
Observables, spectrum 153 158
Observables, sum of 159Ч161
Observables, variable 154
Operators commuting self-adjoint 19
Operators commuting self-adjoint, complete set of commuting self-adjoint 21
Operators commuting self-adjoint, density 4
Operators commuting self-adjoint, positive 291
Operators commuting self-adjoint, spectral representation 293
Operators commuting self-adjoint, spectrum 14
Operators commuting self-adjoint, trace-class 291Ч292
Order relation 96
Orthocomplement 96
Orthocomplementation 96 144
Orthocomplementation, relative 130
Orthomodularity 97 229Ч230
Paradoxes E. P. R. 69Ч72
Paradoxes E. P. R., Schroedinger cat 84Ч86
Pauli matrices 31
Physical quantities compatible 19
Physical quantities compatible, as proposition-valued measures 150
Physical quantities compatible, complementary 26
Physical quantities compatible, complete set of compatible 21
Physical quantities compatible, function of compatible 19
Physical quantities compatible, joint probability distributions 23
Physical quantities compatible, mean value 16
Physical quantities compatible, probability distribution 4Ч5
Physical quantities compatible, probability distribution in a pure state 8
Physical quantities compatible, variance 17
Polytope 211
Polytope, strong 213
POSET 96
Poset, orthocomplete 97
Poset, orthomodular 97
Position of free particle 38
Probability measures 111
Probability measures and covering property 123Ч124
Probability measures, convex combination of 112
Probability measures, dispersion-free 155
Probability measures, on  115 117 118 121 122 115 117 118 121 122
Probability measures, on  114 116 118 121 122 114 116 118 121 122
Probability measures, ordering set of 116
Probability measures, pure 112 122Ч123
Probability measures, separating set of 116
Probability measures, strongly ordering set of 116
Probability measures, sufficient set of 116
Probability measures, superposition of 120
Probability measures, support of 117
Probability space 172 277
Probability space, generalized 278
Projection postulate von NeumannТs 79
Projection postulate von NeumannТs, LuedersТs 79 182 282Ч283
Projection-valued measures 294
Projection-valued measures, spectral 4
Projective geometry 232
Projective lattice 232
Proposition-valued measures 150
Propositions 140Ч142 146Ч149
Propositions, active picture of 187Ч188
Propositions, compatible 155Ч156
Propositions, complementary 162Ч164
Propositions, lattice of 152Ч153
Propositions, ordering 142Ч144
Propositions, orthocomplements 144Ч146
Propositions, orthogonal 148
Propositions, passive picture of 187Ч188
Quantum logic 217Ч225
Quantum superpositions 164Ч167
Quantum superpositions, exchange property of 167
Random variables 155 277Ч278
Rank 194Ч196
Recognition maps 257
Residuated mappings 179
Sasaki projections 99 179
Sasaki projections, properties of 180Ч181
Schroedinger equation 55Ч56
Segment of lattice 130
Spectral theorem 293 295
Spectrum continuous 15 158
Spectrum continuous of observables 153
Spectrum continuous of self-adjoint operators 14
Spectrum continuous, point 14 158
Spectrum continuous, simple 294
Spin 30Ч31
Spin, spin-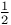 system 31Ч34 system 31Ч34
Spin-statistics connection 65
States of compound systems 65Ч67
States of subsystems 65Ч67 (see also УProbability measuresФ)
States, dispersion-free 155 (see also УProbability measuresФ)
States, exceptional 268Ч271 (see also УProbability measuresФ)
States, mixture 7 (see also УProbability measuresФ)
States, nonpure 7 139
States, pure 7 140
States, superposition of 8 120 164Ч167 191Ч193
States, vector 8 (see also УProbability measuresФ)
StoneТs theorem 55 245 253
Superposition principle 165
Superselection operators 47
Superselection rules 45Ч51 167 238Ч239
Superselection rules and compound systems 73
Superselection rules, continuous 48
Superselection rules, discrete 48
Support 117 299
Tensor product 61 263Ч264
Tensor product, antisymmetrical 64
Tensor product, symmetrical 64
Trace-class operators 291Ч292
Transition probability 12 200
Transition-probability spaces 200
Transition-probability spaces, basis of 202
Transition-probability spaces, orthoclosed subsets of 202
Transition-probability spaces, subspaces of 201
Two-slit experiment 283Ч285
Von Neumann algebras 21 109Ч110
von Neumann algebras, entropy 287
von Neumann algebras, lattices 110
von Neumann algebras, projection postulate 79
Weights 6 112
WignerТs theorem 253
Yes-no experiments 137Ч138 208Ч210
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



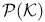


 system
system