|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Bhaya A., Kaszkurewicz E. — Control Perspectives on Numerical Algorithms and Matrix Problems |
|
|
 |
| Предметный указатель |
Lin, Z 231
Linear iterative methods taxonomy of 84
Linear matrix inequality 229
Linear programming problem in canonical form I 160
Linear programming problem in canonical form I, convergence conditions for 161
Linear programming problem in canonical form II, convergence conditions for 161
Linear programming problem in standard form convergence conditions for 164
Linear programming problem, GDS for 154 162
Linear programming problem, GDS for control perspective on 162
Linear quadratic (LQ) 199
Linear quadratic (LQ) problem 8
Linear quadratic (LQ) problem, structurally constrained 208
Linear system of equations,  solution of 141 solution of 141
Linear system of equations, 1-norm (LAD) solution of 141
Linear system of equations, GDS solution of 141
Linear system of equations, GDS solver 131
Linear system of equations, least absolute deviation (LAD) solution of 141
Linear system of equations, least norm solution of 141
Linear system of equations, least squares solution of 141
Linear system of equations, using a GDS for solution of 140
Linear system of equations, weighted least squares solution of 141
Linear system, iterative methods for 71
Linear system, KKT 173
Linear system, underdetermined 144
Lipschitz constant 21
Lipschitz continuous 21
Little, J. B 224 225
LOC (Liapunov optimizing control) 24 45
Locally Lipschitz 21
Logar, A 231
Loss function 140
Loss function, convex 140
Loss function, single-stage 119—121
LQ (linear quadratic) 199
LQ optimal control problem 8
LS-SVM (least squares support vector machine) 173
Luenberger, D. G. xxiv 148 151
Lur’e system 66 68
Machine shop problem, solution via polynomial matrices 230
Majani, E. 174
Mangiavacchi, N. 197
Manocha, D. 219
Marcus, M. 219 223
Marinov, C. A. 174
Markov parameters 11 12
Martin, C. E 227
Martinez, J. M. xxiv 91
Mathis, D 174
Matrix D-stability as feedback stability problem 210
Matrix D-stability for 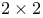 matrices 216 matrices 216
Matrix D-stability for 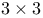 matrices 217 matrices 217
Matrix D-stability sufficient condition in strictly positive real terms 214
Matrix D-stability, characterization for 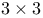 matrices 217 matrices 217
Matrix D-stability, connection to strictly positive real functions 213
Matrix fraction 230
Matrix with rational function entries 230
Matrix, additively diagonally stable 136
Matrix, adjugate 11
Matrix, classical adjoint, definition 11
Matrix, controllability 12 74
Matrix, diagonally stable 17 23
Matrix, dual 12
Matrix, feedback gain 73
Matrix, feedforward 2
Matrix, Hankel 12 15
Matrix, Hurwitz 23
Matrix, Hurwitz diagonally stable 23 26
Matrix, Hurwitz stable 23
Matrix, input 2
Matrix, iteration 75
Matrix, Krylov 12
Matrix, Liapunov equation 229
Matrix, observability 12
Matrix, Schur 17
Matrix, Schur diagonally stable 17
Matrix, Schur stable 17 74
Matrix, system 2
Mattheij, R. M. M 197 224
Mayers, D. F. xxiv
Mayne, D. Q. 118 123 125
McCarthy, C. 200 203
McMillan degree 12 230
McNamee, J. 99
Mehra, P. 132
Metatechnique xxii
Method, backpropagation with momentum (BPM) 83
Method, conjugate gradient (CG) 85
Method, discrete Newton variable structure (DNV) 60 62
Method, feedback gain matrix for 74
Method, Frankel 85
Method, Gauss — Seidel 74 85
Method, Jacobi 74 85
Method, Jacobian matrix transpose (DJT) 61
Method, Jacobian matrix transpose variable structure (DJTV) 61
Method, Krylov subspace 71
Method, Krylov subspace motivation for 71
Method, Newton 117
Method, Newton type optimal control-based 94
Method, Newton-Raphson computational effort of 119
Method, orthodir 85
Method, Orthomin(2) 85
Method, Orthomin(l) 85
Method, preconditioned Richardson 85
Method, Richardson 77
Method, Richardson second-order 85
Method, scalar iterative 66
Method, scalar Newton 67
Method, scalar Newton disturbances acting on 66
Method, scalar Newton effect of disturbances on 66
Method, scalar secant 67
Method, scalar Steffensen 67
Method, spurt 107
Method, steepest descent 79 85 117
Method, successive overrelaxation (SOR) 74 85
Method, variable structure Jacobian matrix transpose (DVJT) 61
Meyer, C. D. 75
Mf (minimum fuel) 95
Minimal realization 12
Minimal realization from Kalman-Gilbert canonical form 15
Minimal residual method, CLF/LOC derivation of 75
Mishchenko, E. 10 39 95
MOCP (multistage optimal control problems) 118
Moliere, J. 24
Momentum factor for BPM 83
Momentum factor for BPM optimal, in terms of CG parameters 84
Momentum parameter for BPM, optimally tuned 83
Monaco, S. 90
Moore, J. B. xxiii 105
Morari, M. 200 211
Morgan, A. P. 219 223 225
Mostowski, A. 219
Multiplier, Lagrange 8
Multistage optimal control problems (MOCP) 118
Murray, D. M. 118 124
Murray, R. 1
Nagao, T. 174
Naidu, D. S. 10
Nash, S. G. xxiv 151
Nedtf, J. 50 90 91
Network weights 83
Neuberger, J. W. 33 39 50
Neural network 132
Neural network as associative memory GDS 134
Neural network as feedback control system 134
Neural network as global optimizer GDS 135
Neural network, discrete-time recurrent 137
Neural network, feedback (recurrent) 132
Neural network, feedforward 132
Neural network, Hopfield — Tank 133
Neural-gradient dynamical system 128
| Neurodynamical optimization 128
Newton method 60
Newton method, disturbances in, Liapunov function approach to 68
Newton method, effect of disturbances on 69
Newton method, effect of roundoff error on 70
Newton method, generalized variable structure 51
Newton method, nonlinear partial 114
Newton method, optimally controlled 96
Newton method, “paradox” of one-step convergence 64
Newton transformation 125
Newton variable (NV) 47—49 53 57 97
Newton vector 125
Newton vector field 52
Newton vector field, extraneous singularities of 52—54
Newton — Raphson method 60
NLP (nonlinear programming problem) 118
Nocedal, J. xxiv 84 151
Nonlinear programming problem (NLP) 118
Nonlinear programming problem (NLP) as multistage optimal control problems (MOCP) 119
Nonlinear programming problem (NLP) to MOCP, general transcription strategy 119
Nonlinearity, first-quadrant-third-quadrant 25 26
Nonlinearity, infinite sector 25 26
Nonlinearity, Normand — Cyrot, D. 90
Nonlinearity, sector 25 26
Ober, R. J. 229
Objective function, penalized 102
Observability matrix 207 221
Observability matrix, nullspace of 13
ODE (ordinary differential equation) 20
ODE (ordinary differential equation) as first-order ODE 87
ODE (ordinary differential equation) existence and uniqueness of solutions 21
ODE (ordinary differential equation) LOC/CLF approach to 87
ODE (ordinary differential equation), CG 85
ODE (ordinary differential equation), HBF 86
ODE (ordinary differential equation), HBF as regularization of Newton ODE 86
ODE (ordinary differential equation), HBF connection to algorithm DC 189
ODE (ordinary differential equation), HBF from CLF approach 89
ODE (ordinary differential equation), Newton 86
ODE (ordinary differential equation), Persidskii type 25
ODE (ordinary differential equation), shooting method for 191
ODE (ordinary differential equation), state space model of 192
ODE (ordinary differential equation), steepest descent 86
ODE integration as parameterized map 180
ODE integration method, asymptotic error estimate 181
ODE integration method, choice of cost function for 187
ODE integration method, constant error generation per time step 190
ODE integration method, global error measures 187
ODE integration method, local error control law 181
ODE integration method, local error model 180
ODE integration method, local error per step (EPS) 181
ODE integration method, local error per unit step (EPUS) 181
ODE integration method, optimal stepsize control constant coefficient ODE 190
ODE integration method, order of 181
ODE integration method, principal error function for 181
ODE integration method, reference method 180
ODE integration method, stepsize control as optimal control problem 187
ODE integration method, stepsize error relation 181
ODE integration method, theoretical results 189
ODE integration, adaptive time-stepping for 179
ODE integration, one step method for 180
Oliveira, R.C.L.F. 210
Ono, T. 197 198
Open loop 3
Optimal conditioning problem 204
Optimal control 9
Optimal control as motivation for variable structure control 94
Optimal control in feedback form 9
Optimal control in knot selection of cubic splines 228
Optimal control in least squares fitting of state space model 228
Optimal control in the theory of Bezier curves 227
Optimal control problem 95 118
Optimal control problem, fixed final state, boundary conditions for 10
Optimal control problem, fixed final time 8
Optimal control problem, free final state 8
Optimal control problem, free final time, boundary conditions for 10
Optimal control problem, linear quadratic (LQ) 8
Optimal control problem, LQ perspective on 208
Optimal control problem, multistage 119
Optimal control problem, singular solution of 111
Optimal control problem, stage of 119
Optimal control theory, elements of 8
Optimal control, steps to find 9
Optimal control, structurally constrained 208
Optimal diagonal preconditioners as decentralized controllers, difficulty of finding 210
Optimal diagonal preconditioning 202
Optimization method, continuous-time 116
Optimization problem, with linear constraints 150
Optimization, benchmark problems for 119
Optimization, CLF approach to 56
Optimization, neurodynamical 128
Optimization, relation to Liapunov function 127
Optimization, second-order dynamical system for classical mechanics analogy for 56
Ordinary differential equation (ODE) as first-order ODE 87
Ordinary differential equation (ODE) as regularization of Newton ODE 86
Ordinary differential equation (ODE) CG 85
Ordinary differential equation (ODE) connection to algorithm DC 1 89
Ordinary differential equation (ODE) existence and uniqueness of solutions 21
Ordinary differential equation (ODE) from CLF approach 89
Ordinary differential equation (ODE) HBF 86
Ordinary differential equation (ODE) LOC/CLF approach to 87
Ordinary differential equation (ODE), Newton 86
Ordinary differential equation (ODE), Persidskii type 25
Ordinary differential equation (ODE), shooting method for 191
Ordinary differential equation (ODE), state space model of 192
Ordinary differential equation (ODE), steepest descent 86
Oren, S. S. 120
Oren’s power function 120
Ortega, J. M 39 66 90 135
Orthomin(l) method, derivation by stabilizing state feedback 77
Output equation 42
Output feedback form 73
Ozan, T. M. 166
O’Shea, D 224 225
Paden, B. 31 39
Pair, {F, G} 3
Panskih, N. P. 107 124
Pantazis, R. D. 228
Parameters of 52
Parisi, V. 56 65 91
Parlett, B. N. 14
Pazos, F. A. xxiv 61
PD (proportional-derivative) 77
Penalty function 147 148
Penalty function parameter, as control gain 149
Peres, P. L. D. 210
Perfect 200
Perfect diagonal conditionability, characterization of 201
Perfect diagonal preconditioning 203 205
Perfect diagonal preconditioning, connection to decentralized feedback 205
Performance index 97
Performance index, minimum fuel (mf) 95
Performance index, minimum time 96
Performance index, quadratic 8
Persidskii, S. K. 25
Persidskii-type system 51
Phansalkar, V. V. 83 91
Phase, convergence 152
Phase, reaching 152
PI (proportional-integral) 7 184
Pickel, P. F 231
PID (proportional-integral-derivative) 6 184
Pinder, G. 224
Pittner, S. 91
Placement, eigenvalue 3
Plant xx 41 43 58 198
PMP (Pontryagin minimum principle) 8
Pogromsky, A. Yu 37 38 51
Polak, E. L. 41 90 118
Pole assignment 74
Pole assignment, regulation 3
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 solution of
solution of 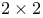 matrices
matrices  matrices
matrices