|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Hale J.K., Kocak H. Ч Dynamics and Bifurcations |
|
|
 |
| ѕредметный указатель |
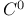 , , 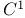 distance 390 distance 390
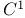 , ,  topology 390 410r topology 390 410r
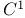 , ,  topology versus topology versus 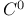 topology 391 topology 391
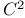 topology 422 topology 422
 function 6 function 6
 function, canonical form 223 (see also УJordan normal formФ) function, canonical form 223 (see also УJordan normal formФ)
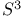 see УThree-sphereФ see УThree-sphereФ
Abelian integral 408
Adjoint equation 254Ч255
Alpha-limit point 183
Alpha-limit point of maps 445
Alpha-limit set 14 183 366 368
Alpha-limit set of maps 445
Analytic vector field 331 339
Animation 530
Annulus 369 487
Area-preserving flow 423
Area-preserving map 260 484Ч493 484 487 493r 502
Area-preserving map, Henon 491
Area-preserving map, linear 484 485
Area-preserving map, piecewise linear 492
Arnold tongues 160 165
Asymptotic phase 342
Asymptotic phase and hyperbolicity 344
Asymptotically stable equilibrium point 17 18 266 267
Asymptotically stable fixed point 73 444 455
Attractor 394 395 439
Attractor dimension 537
Attractor, strange 520 (see also УChaosФ)
Autonomous 4
Averaging 146r
Basin of attraction 277 281 286
BendixsonТs criterion 373 374
Bifurcation and symmetry see УSymmetryФ
Bifurcation at infinity 411r
Bifurcation diagram 28
Bifurcation diagram of harmonic oscillators 210 527
Bifurcation diagram of hysteresis 31 38
Bifurcation diagram of integrable Hamiltonians 527
Bifurcation diagram of logistic map 100
Bifurcation diagram of Poincare Ч Andronov Ч Hopf 212 359
Bifurcation diagram of saddle node 28 36 38
Bifurcation diagram of subcritical pitchfork 35
Bifurcation diagram of supercritical pitchfork 34 38
Bifurcation diagram of transcritical 30
Bifurcation diagram of Van der Pol 351
Bifurcation diagram of vertical 210
Bifurcation diagram, computation of 56Ч61 57 59 60 65r 357Ч360
Bifurcation equation 315
Bifurcation function 315 317 330
Bifurcation function and symmetry 317Ч318
Bifurcation function versus center manifold 330
Bifurcation of conservative systems 425Ч431
Bifurcation of equilibrium see УPitchforkФ УPoincare УSaddle
Bifurcation of fixed point see УPeriod doublingФ УPoincare УSaddle
Bifurcation of gradient systems 436Ч440
Bifurcation of linear systems 247Ч253
Bifurcation of one-periodic equation 133Ч146
Bifurcation of periodic orbit 382Ч386
Bifurcation point 27
Bifurcation set 525
Bifurcation value 27
Birkhoff normal form 486
Boundary-value problem 112
Breaking a saddle connection 210 213 303 304 401 402
Cantor function 159
Catastrophe theory 64r 439
Center 179 180 181 343 416
Center and numerical solutions 463 464 467
Center in Hamiltonian systems 356
Center manifold 321Ч332 321 326 327 332r
Center manifold approximating 325 328
Center manifold for maps 493r
Center manifold versus bifurcation function 330
Center manifold, attraction of 322
Center manifold, depending on parameter 325
Center manifold, nonanalytic 331
Center manifold, nonuniqueness of 330 322
Center theorem of Liapunov 339r 340
Central difference algorithm 464 466
CetaevТs instability theorem 284 305r
Chain rule 540
Chaos 97 99 103r 506 517 520 522r 535r
Chaos in Cremona map 489
Chaos in delayed logistic map 479
Chaos in Duffing 503 507
Chaos in Henon 460
Chaos in Henon Ч Heiles 533
Chaos in logistic map 97 100
Chaos in Lorenz 520
Chaos, onset of 506
Characteristic multipliers 259 260 261 263
Characteristic multipliers, invariance of 261
Characteristic polynomial 230
Characteristic polynomial and trace and determinant 236
Chemical instability 360
Circle map 149 150Ч166 165r 487
Circle map of forced oscillations 501
Circle map, periodic orbits of 155
Circle map, standard 157Ч165 158
Circle, phase portrait on 21 22 54 55
Closed orbit see УPeriodic orbitФ
Codimension-one bifurcation 45 249Ч250 250 251 252
Codimension-one bifurcation with two parameters 46
Codimension-one bifurcation, all planar generic 396Ч403 401 402 411r
Codimension-one singularity 249
Codimension-one submanifold 249 397 541
Codimension-two bifurcation 251 252 405Ч412 407 409 431
Codimension-two singularity 251
Commuting matrices 223
Competing species 171 181
Complete integrability 525 526 531
Complete integrability, analytic versus smooth 535r
Complete integrability, nongenericity of 534r
Composed focus, elementary 398
Computer graphics 529 534r
Conjugate gradient method 440r
Conservation of energy 198
Conservative system structural stability 423
Conservative system, bifurcations in 425Ч432
Conservative system, generic 422
Conservative system, period of 203
Conservative system, second-order 194 198 214 413Ч432 414
Conserved quantity 524 (see also УFirst integralФ)
Constant energy surface 524
Constant momentum surface 525
Continuation of solution 542
Continued fraction 164
Controllable 277
Cremona map 486 488 489 490 491 493
Cremona map, chaos in 489 490
Cremona map, inverse of 491
Critical point 11 415 433 440r
Critical point, degenerate 425 426 438
Critical point, nondegenerate 415 433 438
Critical value 415 525
Cross section see УLocal transversalФ
Cusp 35 36 37 49 84 86 428
Cylinder 118 119 121
Cylinder, invariant 498 499 525
Degenerate critical point 425 426 438
Degenerate equilibrium, cubic 46 53
Degenerate equilibrium, quadratic 44 53
Degenerate equilibrium, quartic 53
Degenerate fixed point, cubic 84
Degenerate fixed point, quadratic 84
Delayed logistic map 455 456 460 493r
Delayed logistic map, chaos in 479
Delayed logistic map, Poincare Ч Andronov Ч Hopf bifurcation in 476 478
DenjoyТs theorem 155 165
| Dense 152 248 251
Dense orbit on torus 154
DevilТs staircase 159 165r
Diffeomorphism 61 186
Differentiable equivalence 61 238
Dimension, four IX 523Ч536
Dimension, one VIII 3Ч104
Dimension, one and one half VIII 105Ч166
Dimension, three IX 511Ч522
Dimension, two VIII 169Ч494
Dimension, two and one half IX 495Ч509 497
Direction field 8 9
Dissipative system 394 394Ч396 411r 508 521
Distance 175
Double zero eigenvalue 239 242 246 406 408 411r
Double zero eigenvalue, unfolding 406 407 411r
Double zero eigenvalue, unfolding linear 250 252
Double zero eigenvalue, unfolding with odd symmetry 408 409 411r
Double zero eigenvalue, unfolding with origin fixed 408
DuffingТs equation 416 418 501Ч509
DuffingТs equation, forced 501 503 509r
DuffingТs equation, forced and damped 506 507
DuffingТs equation, homoclinic tangency in 506
DuffingТs equation, period-doubling in 514
Dulac criterion 373
Dulac function 373 374 387r
Dynamical system VII 7 23r 65r
Ecological models 215r (see also УCompeting speciesФ УDelayed УLogisticФ and
Eigenvalue 229 231
Eigenvalue with negative real part 263 266 267
Eigenvalue, complex 234
Eigenvalue, equal 232
Eigenvalue, purely imaginary 333Ч364
Eigenvalue, real distinct 232
Eigenvalue, zero 307Ч332
Eigenvector 229 231 232Ч237
electrical circuits 172 172Ч174 215r
Elementary composed focus 398 399 401
Elementary homoclinic loop 398 401
Elementary saddle node 397 398 401
Elliptic fixed point 485 502 503
Elliptic fixed point at resonance 488 494r
Elliptic fixed point, stability of 486 493r
Elliptic integral 204
Elliptic integral, numerical computation of 458
Elliptic Umbilic 439
Energy 414
Energy-momentum mapping 525 526
Energy-momentum mapping, bifurcation diagram of 527
Energy-momentum mapping, level set of 525 527
Energy-momentum surface 525 528
entropy 537
Equilibrium point 11 178
Equilibrium point, asymptotically stable 17 266
Equilibrium point, hyperbolic 19 301 391
Equilibrium point, nonhyperbolic 308 334
Equilibrium point, quasi-hyperbolic 398
Equilibrium point, stable 17 266
Equilibrium point, unstable 17 266
Ergodic orbit on torus 528
Ergodic theory 537
EulerТs algorithm 68 104r 463
EulerТs algorithm and hyperbolic limit cycle 467
EulerТs algorithm and linear systems 184 463 464
EulerТs algorithm and logistic map 68
EulerТs algorithm on circle 157
Existence and uniqueness of solutions 6 22r 218 542 543r
FaradayТs law 172
Feedback control 277
Fibonacci numbers 164
Figure eight 416
Figure eight in Duffing 502
First integral 194 196 202 524
First integral for maps 453
First integral, analytic versus smooth 534
First integral, detecting 198
First integral, local 194 203
First integral, nonexistence of 197 535r
First return map see УPoincare mapФ
First-order structurally unstable vector field 397 398 399 400
FISH 416 417
FisherТs Equation 299
FitzHugh neuron model 360
Fixed point 72 444
Fixed point, asymptotically stable 73 444 455
Fixed point, hyperbolic 76 82 83 454
Fixed point, nonbyperbolic 76 77 78 79 84
Fixed point, stable 73 444
Fixed point, unstable 73 444 455
Flip bifurcation see УPeriod-doublingФ
Floating point arithmetic and dynamics 104r 493r
Floquet representation 263
Flow 7
Flow box 186 187
Flow box theorem 185 186 203 375
Flow on torus 147Ч154 153 166r
Fluctuating environment 126
Fold bifurcation 34 (see also УCuspФ)
Foliation 526
Forced Duffing 501 (see also УDuffingФ)
Forced linear oscillator 503
Forced Van der Pol 498 (see also УVan der PolФ)
Forcing function, periodic 498
Fourier series 123
Fractals 494r
FredholmТs alternative 117 255
Frequency locking 165r
Functionally independent 525
Fundamental matrix solution 219 235
Fundamental matrix solution of one-periodic linear system 257
Galaxy model 531
Galileo 174
General position 406
GENERIC 248 252 264r
Generic codimension-one bifurcations 396 401 402 411r
Generic gradient vector field 438
Generic potential function 422 423
Generic properties of Hamiltonians 534r
Generic structural stability 393 411r
Global analysis 23r
Global attractor 394 395
Golden mean 164
Gradient 188 280
Gradient vector field 12Ч14 15 23 188 432Ч442 433 435 436 440r
Gradient vector field, bifurcations of 436
Gradient vector field, generic 438
Gradient vector field, linear 438
Gradient vector field, omega-limit set of 434
Gradient vector field, unfolding of 439
Grobman Ч Hartman theorem 301 305r 493r
GronwallТs inequality 269 270
Hamiltonian system 198 423 494r 523Ч536 524 534r
Hamiltonian system, completely integrable 525 526 534
Hamiltonian system, nonintegrable 531 533
HamiltonТs equations 524
Hard spring 204
harmonic oscillator see УLinear harmonic oscillatorФ
Hartman Ч Grobman theorem see УGrobman Ч HartmanФ
Harvesting, constant 40
Harvesting, periodic 128
Harvesting, proportional 40
Henon map 458 459 460 493r
Henon map and logistic map 461 465
Henon map and Poincare Ч Andronov Ч Hopf bifurcation 483
Henon map, area-preserving 491
Henon map, attractor of 459 460 461
Henon map, inverse of 461
Henon map, period 7 orbit of 471
Henon map, period doubling in 471 472
Henon map, saddle-node bifurcation in 470
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



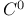 ,
, 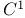 distance
distance  topology
topology 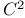 topology
topology  function
function