|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Balachandran V.K. — Topological Algebras. Volume 185 |
|
|
 |
| Предметный указатель |
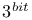 3.7.3 3.7.3
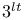 3.7.3 3.7.3
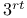 3.7.3 3.7.3
 = a commutes with b : ab=ba 1.1.7 = a commutes with b : ab=ba 1.1.7
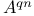 1.7.13 1.7.13
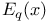 5.2.6 5.2.6
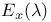 5.2.10 5.2.10
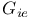 5.2.7 5.2.7
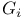 1.1.4 1.1.4
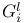 3.7.1 3.7.1
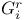 3.7.1 3.7.1
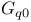 5.2.7 5.2.7
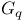 1.1.17 1.1.17
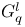 3.7.1 3.7.1
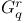 3.7.1 3.7.1
 3.6.16 3.6.16
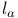 2.2.2 2.2.2
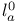 3.6.1 3.6.1
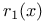 6.6.1 6.6.1
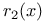 6.6.1 6.6.1
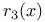 6.6.1 6.6.1
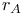 2.2.2 2.2.2
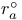 3.6.1 3.6.1
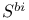 3.7.1 3.7.1
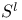 3.7.1 3.7.1
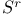 3.7.1 3.7.1
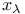 6.2.1 6.2.1
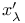 6.3.1 6.3.1
 1.3.1 1.3.1
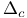 2.2.18 2.2.18
 1.6.1 1.6.1
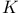 1.6.1 1.6.1
 1.6.1 1.6.1
 -independent 1.5.20 43 -independent 1.5.20 43
 -bounded 4.3.9 192 -bounded 4.3.9 192
 -complete 3.1.20 106 -complete 3.1.20 106
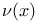 3.3.7 3.3.7
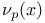 3.3.5 3.3.5
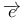 5.2.1 5.2.1
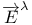 5.2.1 5.2.1
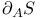 8.23 8.23
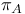 8.3.1 8.3.1
 -admissible function 5.4.7 241 -admissible function 5.4.7 241
 -admissible holomorphic 5.4.11 245 -admissible holomorphic 5.4.11 245
 -Banach A-module 9.3.3 417 -Banach A-module 9.3.3 417
 -Banach algebra 3.4.4 132 -Banach algebra 3.4.4 132
 -Banach space 3.2.6 111 -Banach space 3.2.6 111
 -convex linear combination 4.1.1 174 -convex linear combination 4.1.1 174
 -guage 4.1.8 178 -guage 4.1.8 178
 -modulus homogenity condition 3.2.1 110 -modulus homogenity condition 3.2.1 110
 -normed LS 3.2.6 111 -normed LS 3.2.6 111
 -seminormed LS 3.2.6 111 -seminormed LS 3.2.6 111
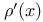 1.7.5 1.7.5
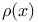 1.7.1 1.7.1
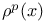 6.3.1 6.3.1
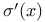 1.7.5 1.7.5
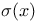 1.7.1 1.7.1
![$\sqrt[ch]{A}$](/math_tex/c9edfecfa7ab54e9cb4c6b3d9fdc3d0a82.gif) 2.218 2.218
![$\sqrt[h]{A}$](/math_tex/230577f7222567fe2495eebbe767b99682.gif) 1.3.7 1.3.7
![$\sqrt[s]{A}$](/math_tex/fd67092a96f1e7203ef6f98be71dfa1b82.gif) 1.5.11 1.5.11
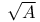 1.2.24—1.2.25 1.2.24—1.2.25
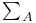 8.3.1 8.3.1
(F) algebra 3.3.13 123
(F) norm 3.1.14 105
(F) space 3.1.14 105
(l., r.) Primitive ideal 1.5.4 38
A-module 1.5.1 36
Absolutely convergent series 3.1.23 109
Absolutely p-convex 4.1.1 174
Absorbing set 2.1.15 78
Almost submultiplicative (a.sm.). function 3.3.3 118
Ample algebra 4.7.1 213
Annihilator (left, right) 1.2.1 12
Arens algebra 4.6.8 (iv) 211
Arens — Calderon trick 8.5.18 394
Bi-ideal 1.2.1 12
Bi-primitive ideal 1.5.4 38
Bi-singular 3.7.1 158
Binomial theorem 1.1.7 3
Boolean algebra 8.6.7 407
Bound of a linear transformation 3.5.1 140
Bounded or n. (=norm) bounded linear transformation 3.5.1 140
C algebra 3.6.4 148
Canonical character 1.4.10 36
Canonically  -normed function algebra 8.1.1 353 -normed function algebra 8.1.1 353
Cauchy net or C-net 2.3.1 91
Cauchy's estimates 5.4.18 252
Cauchy's integral theorem 5.4.16 249
CHARACTER 1.3.1 22
CI algebra 3.6.20 3.6.21 153
Circle operation 1.1.13 6
Closed graph theorem 3.1.16 105
Closed map 3.1.16 105
Commutant 1.1.7 3
Complete p -topology 3.1.4 101
Complete quarter-norm 3.1.13 105
Complete topological linear space (complete TLS) 2.3.1 91
Completely regular algeba 8.4.1 377
Completely regular family of functions 8.4.8 381
Complex structure 1.6.1 43
contour 5.4.15 248
Contour surrounding a subset 5.4.15 248
Contraction 4.3.14 194
Contraction mapping principle 4.3.15 194
Convergence of series and generalized series 2.1.32 83
CQ algebra 3.6.20 3.6.21 153
Cyclic module 1.5.13 41
Derivation 7.6.5 345
Directed set 2.1.1 73
Discrete 2.1.11 78
Distinguished character 1.4.10 36
Distributive lattice 8.6.7 407
E(X) 5.2.1
Entire functions operating in a topological algebra (TA) 5.5.1 253
Epimorphism 1.1.10 4
Equivalence of subadditive (sad.) functionals 3.1.4 101
Essentially bounded net 2.3.5 93
Essentially nilpotent element 1.2.25 22
Examples of,  -Banach algebras 3.4.6 133 -Banach algebras 3.4.6 133
Examples of,  -seminormed algebras 3.4.6 133 -seminormed algebras 3.4.6 133
Examples of, (F) algebras 3.3.14 123
Examples of, Completely regular algebras 8.4.2 378
Examples of, Fixed ideals 8.1.17 8.1.18 8.1.23 354 360
Examples of, Function algebras 8.1.2 353
Examples of, Hypermaximal ideals 1.3.13 25
Examples of, Metrizable locally pseudoconvex algebras 4.6.8 209
Examples of, Monogenic topological algebras 7.3.22 321
Examples of, Primary ideals 7.1.20 301
Examples of, Shilov algebra 8.6.13 409
Examples of, Shilov boundary 8.2.16 367
Exponential function 5.2.1 227
Extended quasi-resolvent 1.8.1 61
Extended quasi-spectrum 1.8.1 61
Extended spectral radius 1.8.10 64
Extended spectrum 1.8.1 61
Faithful quarter-norm 3.1.14 105
Faithful representation 1.5.1 36
Faithful sad. functional 3.1.1 100
Fixed ideal 8.1.17 357
Formally real algebra 1.6.17 50
Function algebra 8.1.1 353
Functionally continuous 2.2.19 90
Gelfand algebra 7.2.1 303
Gelfand lemma 3.3.6 119
Gelfand space 7.3.1 311
Gelfand transform 7.3.4 312
Gelfand — Beurling (GB) algebra 7.4.1 324
Generalized sum 2.1.32 83
Hilbert relation 6.2.2 264
Homogenity index of a pseudo-seminorm 3.2.1 110
| Homomorphism 1.1.10 4
Hull-kernel topology (hk-topology) 8.3.5 371
Hyper semi-simple (h.s.s.) 1.3.7 24
Hyper-radical 1.3.7 24
Hypermaximal ideal 1.3.6 24
Hypernormal TA 7.1.4 297
Hyponormal TA 7.1.4 297
I algebra 3.6.7 149
Ideal (l., r.) 1.2.1 12
Index of a point 5.4.15 248
Inverse (l. r.) 1.1.3 1
Inverse-closed subalgebra 1.7.27 61
Irreducible module 1.5.2 1.5.13 37 41
Isomorphism 1.1.10 4
Jacobson density theorem 1.5.21 43
Joint spectrum 8.5.7 389
Ker  . 3.1.20 106 . 3.1.20 106
Ker p. 3.1.5 102
Lattice 8.6.7 407
Leibniz rule 7.6.8 346
Lemma (Bonsall — Duncan) 9.4.1 419
Linear functional 1.3.1 23
Liouville algebra 1.8.13 65
Locally  -admissible holomorphic 5.4.12 245 -admissible holomorphic 5.4.12 245
Locally bounded algebra 4.2.4 (f.n.) 187
Locally bounded space 2.1.24 81
Locally pseudo-convex algebra 4.4.1 195
Locally pseudo-convex space 4.3.1 189
Locally sm. pseudo-pre-Frechet (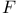 ) algebra 4.6.3 208 ) algebra 4.6.3 208
Michael algebra 4.5.4 204
Minimal pre-boundary 8.2.3 362
Monogenic 7.3.21 320
Monomorphism 1.1.10 4
Net 2.1.1 73
Norm bounded (n bounded) 3.2.12 3.5.1 114 140
Normal family of functions 8.4.8 381
Normal TA 7.1.4 297
Normalized  -seminorm 3.4.13 136 -seminorm 3.4.13 136
Nucleus 2.1.9 77
Open mapping theorem 3.1.15 105
Operator topology 2.2.4 85
p-bounded 3.2.12 114
Polynomially convex (p. convex) 8.5.1 388
Polynomially convex hull 8.5.1 388
POSET 2.1.1 73
Power series operating in a TA 5.5.1 253
Pre-(F) algebra 3.3.13 123
Pre-boundary 8.2.1 361
Primary ideal 7.1.18 301
Prime ideal 1.5.9 (f.n.) 39
Principal class 2.3.9 95
Principal component 5.2.7 230
Projective limit 4.5.1 201
Pseudo Frechet (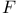 ) algebra 4.26.2 208 ) algebra 4.26.2 208
Pseudo-convex algebra 4.4.1 195
Pseudo-convex space 4.3.1 189
Pseudo-pre-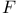 algebra 4.6.2 208 algebra 4.6.2 208
Pseudo-resolvent function 6.3.1 275
Pseudo-resolvent set 6.3.1 275
Quarter-norm 3.1.8 103
Quarter-normed algebra 3.3.1 116
Quasi semi-simple (q.s.s) 1.7.17 57
Quasi-inverse, Quasi-invertible 1.1.16 6 7
Quasi-nilpotent (q.nilpotent) 1.7.13 56
Quasi-resolvent set 1.7.5 54
Quasi-spectrum 1.7.5 54
Quasi-square root (q.sq.r.) 5.3.1 235
Quasi-unital 8.3.15 375
R(X) 1.8.10
Radical (Jacobson) 1.2.25 22
Radical algebra 1.2.27 22
Radius of convergence 5.1.6 223
Real character 1.6.14 49
Regular bi-ideal 1.2.6 14
Regular ideal (l. r.) 1.2.6 14
Regular representation 1.5.1 36
Relative bi-unity 1.2.6 14
Relative unity (l., r.) 1.2.6 14
Resolvent set 1.7.1 52
Rickart separating function 9.2.1 412
Saturated closure 4.3.7 191
Saturated family of pseudo-seminorms 4.3.7 191
Self-conjugate (subset, ideal) 1.6.4 1.6.12 44 46
Semi-metric space 3.1.2 (f.n.) 100
Semi-simple (s.s.) 1.2.27 22
Semi-topological group 2.2.6 (f.n.) 86
Separating element 9.2.4 414
Separating function (Rickart) 9.2.1 412
Separating, strongly separating, family of functions 8.1.12 356
Shilov algebra 8.6.12 409
Shilov boundary 8.2.3 362
Simple module 1.5.2 (f.n.) 37
Simultaneous spectrum 8.5.7 389
Singular (l., r.) 3.7.1 158
sm. pseudo-convex algebra 4.4.1 195
Spectral radius 1.8.10 64
Spectrally connected 8.6.14 409
Spectrally Gelfand 7.2.5 304
Spectrum of an algebra 7.3.1 311
Spectrum of an element 1.7.1 52
Strictly real algebra 1.9.1 67
Strong structure space 8.3.9 372
Strongly analytic function 5.1.3 222
Structure space 8.3.9 372
Submultiplicative (sm.) function 3.3.3 118
Subnet 2.1.1 73
Support of a function 8.4.24 (f.n.) 386
Symmetric subset of a group 2.1.3 74
Symmetric subset of C 1.8.3 (f.n.) 62
Theorems of, Arens (Proposition) 3.3.2 116
Theorems of, Arens — Banach 3.6.16 152
Theorems of, Arens — Shilov (Cor.) 6.5.20 290
Theorems of, Banach — Steinhauss 3.2.16 115
Theorems of, Beurling — Gelfand (spectral radius formula) 6.2.11 271
Theorems of, Beurling — Gelfand — Zelazko 7.4.6 326
Theorems of, Birkhoff — Kakutani 2.1.7 76
Theorems of, Bonsall — Duncan 3.5.9 144
Theorems of, Gelfand (norm equivalence theorem) 9.1.4 412
Theorems of, Gelfand — Kolmogorov — Stone — Banach 8.1.22 359
Theorems of, Gelfand — Mazur 6.5.5 285
Theorems of, Gleason — Kahane — Zelazko 5.2.15 233
Theorems of, Jacobson (density theorem) 1.5.21 43
Theorems of, Johnson 9.4.2 9.4.3 420 423
Theorems of, Kaplansky 1.9.15 71
Theorems of, La Page — Hirschfield — Zelazko 7.4.15 331
Theorems of, Michael 4.5.3 7.4.8 202 327
Theorems of, Mitjagin — Rolewicz — Zelazko (Cor) 5.5.11 261
Theorems of, Nagumo 5.2.14 232
Theorems of, Oka (extension theorem) 8.5.19 396
Theorems of, Rickart 4.1.16 183
Theorems of, Shilov (idempotent theorem) 8.6.4 404
Theorems of, Shilov — Arens — Calderon 8.5.22 399
Theorems of, Singer — Wermer 7.6.20 351
Theorems of, Turpin 6.6.5 294
Theorems of, Tychnoff 2.1.12 78
Theorems of, Wiener — Levi — Zelazko 7.5.16 (b) 342
Theorems of, Wiener — Zelazko 7.5.16 (a) 342
Theorems of, Yood (Proposition) 7.4.20 333
Theorems of, Zelazko 5.5.10 259
Topological A-module 9.3.1 416
Topological group (TG) 2.1.3 74
Topological integral domain (TID) 6.3.13 281
Topological linear space (TLS) 2.1.9 77
Topological nilpotent (t.nilpotent) 4.8.8 220
Topological semigroup (TSG) 2.2.5 (f.n.) 86
Topological spectral radius 4.8.1 216
Topological zero divisor (generalized (g.t.z.d.)) 3.7.38 172
Topological zero divisor (l., r., bi-) 3.7.3 158
Topological zero divisor (symmetric (s.t.z.d.)) 3.7.11 162
Universal mapping properly 4.5.1 201
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



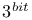
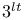
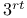
 = a commutes with b : ab=ba
= a commutes with b : ab=ba 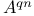
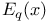
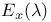
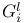
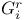
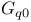
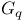
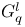
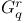

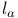
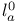
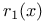
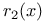
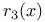
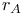
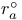
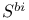
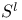
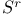
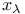
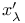

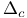

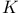

 -independent
-independent  -bounded
-bounded 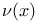
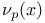
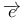
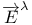
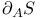
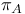
 -admissible function
-admissible function 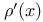
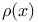
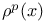
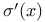
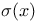
![$\sqrt[ch]{A}$](/math_tex/c9edfecfa7ab54e9cb4c6b3d9fdc3d0a82.gif)
![$\sqrt[h]{A}$](/math_tex/230577f7222567fe2495eebbe767b99682.gif)
![$\sqrt[s]{A}$](/math_tex/fd67092a96f1e7203ef6f98be71dfa1b82.gif)
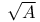
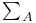
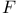 ) algebra
) algebra