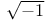|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Berkeley H. Ч Mysticism in Modern Mathematics |
|
|
 |
| ѕредметный указатель |
Abstraction as a mental process 159
Abstraction, assumption not relevant to 177
Abstraction, function of, in relation to articulate sounds 11
Abstraction, perception or imagery a condition of 159
Algebra as Arithmetica Universalis 121 123 126
Algebra, laws of 87
Algebra, relation to arithmetic 80 81
Algebraic Factors, not expressive of algebraic quantities, no 118
Algebraic Multiplication in relation to power and root 104 118
Algebraic Multiplication, current explanation of 99 100
Algebraic Multiplication, mystical view of 103
Algebraic Multiplication, not an extension of the arithmetical notion 117
Algebraic Multiplication, sophisms involved in this explanation 99Ч102
Algebraic Multiplication, unintelligibility of, save as a dual process 102Ч104
Algebraic Quantity and the Law of Association 86 88Ч89 116
Algebraic Quantity as synthesis of two distinct relations 120
Algebraic Quantity, nature of the notion of 98
Algebraic Quantity, symbolization of the series of 97
Analogy as the foundation of explanation 220
Angle, the, analysis of the notion of 166Ч167
Association, mnemonic, in relation to symbolism of numeration 60
Assumption in relation to existence of geometrical entities 173Ч174
Assumptions and definitions, confusion between 162 note
Assumptions, the, alleged to be made by Euclid 172 182
Axiom of Parallels as a generalization from experience 194
Axiom of Parallels, alleged uncertainty of 192
Axiom of Parallels, broken up into two subordinate propositions 192
Axiom of Parallels, CayleyТs view of 193 240
Axiom of Parallels, close analogy of these with axioms of magnitude 195Ч196
Axiom of Parallels, EuclidТs statement of 191Ч192
Axiom of Parallels, logically equivalent to two axioms of direction 195
Axiom of Parallels, neither a definition nor an axiom 191Ч192
Axiom of Parallels, self-evident but not axiomatic 255
Axiom of Parallels, suggestion of the empirical in EuclidТs form of 195
Axioms are synthetic and apodeictic judgements 175
Axioms in geometry, definition of 186 254
Axioms in relation to magnitude and direction 254
Axioms of magnitude, Poincare on 174
Axioms, EuclidТs sub-sumable under two general propositions 186Ч189
Axioms, F. Klein, on nature of 179
Axioms, the veductio ad absurdum argument in connexion with 189 190
Binet, A. on perception and reasoning 42
Boole, G. on conditions of valid reasoning by the aid of symbols 77Ч78
Boole, G., criticism of 78Ч79
Calculus, interpretable in another field of thought 82
Calculus, uninterpreted(Whitehead) 75
Cayley, A. of DistanceФ 239Ч242
Cayley, A. on mathematical ima-ginaries 64 65 67Ч70 251
Cayley, A. on the axiom of parallels 193 240
Cayley, A., metaphysical outlook upon the fundamental notions of mathematics 72Ч73
Cayley, A., relation to non-Euclidean geometry 241 242
Chasles on geometrical imaginaries 128Ч130
Chrystal, G. on algebraic equality 95
Chrystal, G. on algebraic multiplication 99 100 101
Chrystal, G. on algebraic quantity and law of association 88Ч89
Chrystal, G. on heterogeneity of positive and negative quantity 92Ч93
Chrystal, G. on imaginary quantity 113 114
Chrystal, G. on the relation of power and root 107 110
Chrystal, G. on the series of algebraic quantity 97
Clifford, W.K. on elementary flatness of surface 220 221
Clifford, W.K., analogous conception in relation to space 222
Clifford, W.K., analysis of the axiom of free mobility 199Ч203
Clifford, W.K., criticism of this analysis 199Ч203
Clifford, W.K., popular exposition of metageo-metry 219Ч222
Clifford, W.K., views criticized 220Ч222
Conant, Professor, on the nature of the number-concept 56Ч59
Concept and meaning 69
Concept, definition of(Dictionary of Philos. and Psych.) 46
Congruence in Geometry 158
Congruence, assumption of, relevant to mensuration, meaningless in relation to geometry 199 203
Congruence, criticism of explanation of, as a geometrical assumption by (1) Clifford 199Ч203
Congruence, criticism of explanation of, as a geometrical assumption by (2) Russell 203Ч205
Congruence, EuclidТs alleged tacit assumption of 198Ч199
Congruence, so-called axiom of, and EuclidТs Axiom 1 205 255
Congruence, verbal equivalents of the notion of 205
Contingent Relations in Geometry, principle of 128Ч130
Contingent Relations, same as PonceletТs principle of continuity 130
Contradiction, real and nominal 206Ч207
Conventionality of language 12
Conventions in Algebra, import of 81
Conventions, validity of 81
Couturat, L. on the foundations of geometry 154Ч157
Couturat, L. on the role of intuition in geometry 169
Couturat, L., views criticized 154Ч157
Darwin and Max MullerТs views on language 24
Definition and meaning 14 15
Definition of geometry 152
Definition of space useless 154
Definition, limit of process of 4 14
Definition, nature and function of, compared 18
Definition, real nature of 16 17
Definition, Riemann on, in geometry 223
Definition, technical sense of, in geometry 154
Demonstration, nature and object of, in geometry 169Ч171
Demonstration, R. Sim-son on 169
Demonstration, the Epicureans and 169 170
Direction, notion of, in connexion with non-Euclidean spaces 248Ч249
Direction, notion of, involved in the conception of linear shape 168 254
Direction, relation to notion of straightness 160 162 163
Distance, ambiguity of term in relation to descriptive principles in geometry 241 257
Elementary Flatness of space 222
Elementary Flatness of surface 220Ч221
Epicureans, the, and the object of demonstration in geometry 169 170
Equality of spaces, notion of, derived from congruence of figurer 199
Existence, meaning of, in relation to geometrical entities 173Ч174
Factors in Algebra not expressive of algebraic quantities, no 118
Fran5ais, J.F. on the representation of imaginary quantities 121
Free mobility see Congruence
Galton, F. on thought without words 28 39 40
Geometry, a priority of (Russell) 164 and note
Geometry, CliffordТs definition of 199 253
Geometry, imaginary elements of 65 68Ч73 Chap.
Geometry, non-Euclidean, origin of 153
Geometry, not a physical science 253
Geometry, premisses of 255
Geometry, pure, relation of symbolism to 6
Geometry, systems of, and the relevance of truth to 178
Hamilton, Sir W.R. on derivation of concept of number 56
Hamilton, Sir William, on language as an aid to thought 27Ч29
Helmholtz on RiemannТs conception of manifoldness 230
Helmholtz, analogical value of УFlat-landФ and УSpherelandФ 218 219
Helmholtz, fallacies involved in this exposition 216Ч218
Helmholtz, popular exposition of metageometry 213Ч219
Henrici, O. on EuclidТs assumptions 172
Henrici, O. on EuclidТs axioms of magnitude 187
Henrici, O. on imaginary loci 131Ч133
Homonymy in relation to algebraic expression 90
Image, representative and symbolic, functions of, in the development of thought 42Ч44 250
Imaginaries, mathematical, doctrine of Chap. VI
Imaginaries, nature of enigma involved in, according to (1) Cayley 68 69 70 85
Imaginaries, nature of enigma involved in, according to (2) Whitehead 79 85
Imaginary, loci 69 71
Imaginary, loci, geometrical doctrine of Chap. IX
Imaginary, objects (of geometry) in relation to experience 73
Imaginary, point, notion of, how arrived at analytically 69
Imaginary, point, notion of, how arrived at geometrically 70
Imaginary, points, a УfactorФ in the definition of real geometrical relations 135
Imaginary, points, derivation of, in analytical geometry 142Ч145
Imaginary, points, introduction of, in geometrical involution 132Ч134
Imaginary, quantity 69
Imaginary, quantity, textbook derivation of the notion, and sophisms involved in this derivation 113Ч115
Imaginary, quantity, two senses of the УinterpretationФ of, in geometry 146Ч147
Imaginary, unit, a УfactorФ in the expression of algebraic quantity 126
Indefinables in mathematics 154 156
indices see УPower and RootФ
Intercommunication, presupposition involved in 4 8 10
Intuition, role of, in geometry 169 170
Involution in geometry 132Ч134
Kantians and non-Euclidean geometry V
Klein, F. on nature of geometrical axioms 179
| Klein, F. on RiemannТs conception of space 184
Klein, F., connexion of CayleyТs Theory of Distance with Metageometry 241 242
Language and thought Chap. II
Language as a potential source of illusory beliefs 13
Language as an instrument of reason Chap. III
Language, essentially conventional nature of 9
Language, functions of, as embodiment of acquired knowledge and as aid in reasoning 29 46Ч47
Language, learning of, mechanical by comparison with origination and development of 11
Language, not a necessary condition of forming abstract ideas 12 46
Language, subjective and objective aspects of 15 18 19 49
Language, the original and instinctive in expression replaced by the artificial and conventional 10
Laws are symbolic of processes of thought 87
Laws of Algebra, no difference between, and conventions of same 81
Length, EuclidТs conception of, as involved in his definition of the line 167
Length, RussellТs derivation of the notion 167
Length, RussellТs derivation of the notion, inadmissible 167Ч168
Light, rectilinear propagation of, in relation to geometrical theory 246Ч247
Linear shape, analysis of the notion of 168
Lobatschewsky and the conception of the straight line 181
Lobatschewsky on astronomical observations as a test of geometrical theory 244
Lobatschewsky, his geometry in relation to the modifiability of the conception of space 211Ч212
Lobatschewsky, his hypothesis regarding parallels 207
Lotze on the futility of astronomical observations as a test of geometrical theory 244
Lotze, ineffectiveness of his attack on non-Euclidean geometry 218
Lotze, RussellТs criticism of 245
Love, A.E.H., on number and quantity 61Ч62
Manifoldness, ambiguities in definition of 229Ч231
Manifoldness, continuous, positions and colours 229
Manifoldness, notion of (Helmholtz) 230
Manifoldness, notion of (Riemann) 229
Manifoldness, relation of notion of, to that of space 257
Mathematics, apparent sophistry and paradox in 6Ч7
Mathematics, symbolism in relation to 6
Mathematics, the domain of definite and stable concepts 6
Max Muller and Whitney, conflicting views of language harmonized 48Ч49
Max Muller, doctrine of the identity of thought and language 20Ч26
Max Muller, his doctrine in conflict with DarwinТs views 24Ч25
Max Muller, names as an essential element of thought 21Ч22
Max Muller, sense in which he uses the terms УidentityФ and УinseparablenessФ 21
Max Muller, words the signs of concepts not of things 23
Meaning and definition 14
Meaning and symbol, mutually constituted by association 8
Meaning and thought, difference between 8
Meaning of an idea 72
Meaning, stability of, in relation to symbol 13
Measure of Curvature as an inherent property of surface 235Ч236
Measure of Curvature, a metaphorical expression in relation to a manifold, and to space 233Ч234
Measure of Curvature, fallacious analogy between surface and space 237Ч238
Mensuration, relation of, to metrical geometry 243Ч248 258
Metaphor, expression of analogy 18
Metaphysics, effect of conflict of systems of 3
Metaphysics, value of, as an intellectual exercise 3
Mill, J.S. on the existence of, and the conception of, geometrical entities 163 note
Mill, J.S. on the nature of definition 16
Mill, J.S. on the truths of geometry 72
Mill, J.S., TaineТs criticism of 16
Muscular Adjustment, function of, in perception of shape 160Ч161
Mystical Illusion in geometry as in algebra, prompted by anterior use of semi-paradoxical expressions 136
Mystical Tendency in geometry as compared with algebra 131 142
Mysticism and symbolic ratiocination 5 65 71 93 95 102 118
Mysticism and the Pythagoreans iii
Mysticism in the derivation of mathematical notions 64
Mysticism, influence on, of psychological investigation iv;
Mysticism, special sense of the term 5 note
Names and concepts 23
Names and things 16 23
Names of numbers of geometrical shapes 158Ч159
Names of numbers, interdependence of definitions of 54 note
Names, functions of, in the development of conception 44 250
Names, how their import and purpose are learnt 11
Names, J.S. Mill and Taine on function of 16
Names, meanings of, relative to purpose 34
Names, metaphorical employment of 35
Nature, discussion on Уthought without wordsФ quoted from 39Ч41
Number and quantity in algebraic symbolism 63
Number and quantity in the abstract 61Ч62
Number as conceived by the civilized man and by the savage 57 58
Number as such neither positive nor negative 116
Number, conception of 53Ч54 251
Number, Cou-turat and Russell on the definition of 54 note
Number, interdependence of concepts of 54
Number, relation of, to conception of order 55Ч56
Number, serial association of signs common to all systems of expressing 60
Number, the defining of symbols of 54 and note
Number, transition from representation to symbolism of 58Ч60
Numbers as co-ordinates in geometry 242
Numerals and the use of the fingers to express numbers 59
Paradox as a means of expressing real relations 130 132 134 135Ч136
Paradox, inception of in the metaphorical expression of real relations 141
Paradox, sanction of 147
Paradox, test of valid use of 253
Particular, the, and the general, unthinkable save in relation to one another 155Ч156
Perception of shape 160Ч161
Perception, a rudimentary process of reasoning (Binet) 42
Perpendicularity, EuclidТs alleged assumption of the existence of 180
Perpendicularity, irrelevance of demonstration to this symbolization 125
Perpendicularity, relation of, symbolized by 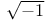 122 122
Plane, extension of the meaning of term 211
Plane, name of an identity of surface-shape 158
Plane, the, as standard of comparison 159
Plane, the, empirical origin of conception of 163
Poincare, H. on nature of synthetic judgements a priori 176
Poincare, H. on the existence of mathematical entities 174
Poincare, H. on the nature of geometrical axioms 175Ч177
Poincare, H. on the validity of Euclidean geometry 245
Poincare, H., the fundamental axioms of geometry 176
Postulates, EuclidТs are complementary definitions of the straight line and circle 182Ч183
Postulates, nature of, in EuclidТs Elements 182Ч185
Power and Root and relations of algebraic quantity 108Ч109
Power and Root and the employment of indices 107Ч108
Power and Root, arithmetical definition of 106
Power and Root, implied algebraic definition of 106Ч107
Power and Root, inconsistency in the use of indices of 108Ч109 111 118
Power and Root, validation of this inconsistency 108 111 112 119
Pragmatism as a solvent of mysticism iv
Properties of space, ambiguity of the term 151Ч152
Pythagoreans, the mental characteristics iii
Quantities, conventional test of inequality 93 116
Quantities, positive and negative, alleged heterogeneity of 93 116
Quantities, sophisms involved in this test 94Ч97
Quantity, not, as such, either positive or negative 116 120 122
Quantity, vicious reaction of algebraic symbolism on the notion of 252
Reasoning of animals 30 32Ч33 35
Reasoning of animals, compared with man 35
Reasoning, process of, in relation to typical imagery and to symbolic imagery 5
Reasoning, subjects of, distributable between two extremes 5
Reasoning, with and without the aid of words 39Ч41
Reid on definition 14
Riemann, conception of space as finite but unbounded 184
Riemann, his alternative to EuclidТs Axiom 10 226
Riemann, outline of dissertation on foundations of geometry 223Ч224
Riemann, outline of dissertation on foundations of geometry and criticism of the filiation of ideas in 224Ч226
Riemann, relation of his mathematical analysis to this notion 232
Riemann, relation of his mathematical analysis to this notion and of space to this notion 232
Riemann, the notion of manifoldness and its obscurities 227Ч232
Right Angle, the see Perpendicularity
Russell, B.A.W. criticism of Lotze 245
Russell, B.A.W. on algebraic imaginaries 74 83 note
Russell, B.A.W. on congruence and rigid bodies 204
Russell, B.A.W. on Helm-holtzТs УFlatlandФ and УSphere-landФ 218
Russell, B.A.W. on intuition in geometry 170
Russell, B.A.W. on the axiom of congruence 203Ч205
Russell, B.A.W. on the axiom of parallels 192
Russell, B.A.W. on the derivation of the notion of length 167
Russell, B.A.W. on the irrelevance of motion to the foundations of geometry 204
Russell, B.A.W. on the reduction of metrical to projective principles 242 note
Russell, B.A.W. on the relation between different space-constants 237Ч238
Signs, rule of, in algebra 90Ч91 98Ч99
Simson, R. on demonstration in geometry 169
Smith, H.J. Stephen on the nature of LobatschewskyТs assumption 207
|
|
 |
| –еклама |
 |
|
|
 |
 |
|
 |
|
ќ проекте
|
|
ќ проекте