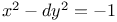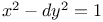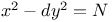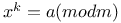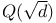|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Adler A., Cloury J.E. — Theory of Numbers: A Text and Source Book of Problems |
|
|
 |
| Предметный указатель |
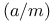 Jacobi symbol 151 Jacobi symbol 151
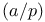 Legendre symbol 129 Legendre symbol 129
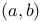 greatest common divisor 8 greatest common divisor 8
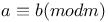 a congruent to b modulo m 40 a congruent to b modulo m 40
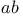 a does not divide b 7 a does not divide b 7
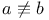 (mod m) a not congruent to b modulo m 40 (mod m) a not congruent to b modulo m 40
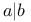 a divides b 7 a divides b 7
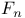 nth Fermat number 198 nth Fermat number 198
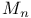 nth Mersenne number 197 nth Mersenne number 197
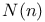 number of representations of n as a sum of two squares 228 number of representations of n as a sum of two squares 228
![$[a, b]$](/math_tex/bd4455e79810acc06e3d31c60fb8bfb282.gif) least common multiple 9 least common multiple 9
![$[x]$](/math_tex/7e1c4a3a07c941625c2f20c594cb9f7c82.gif) greatest integer not exceeding x 13 greatest integer not exceeding x 13
 Euler Euler  -function 75 -function 75
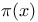 number of primes not exceeding x 200 number of primes not exceeding x 200
 sum of positive divisors of n 12 sum of positive divisors of n 12
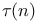 number of positive divisors of n 12 number of positive divisors of n 12
Al-Karaji 221
al-Khwarizmi 7
Algebra (Euler) 356
Approximations to  284 301 284 301
Approximations, best rational 284
Approximations, rational 282
Arithmetica (Diophantus) 267
Aryabhata 37
Associate 358 367
Bachet, Claude 6
Bertrand's postulate 201
Bhaskara 355
Binary gcd algorithm 36
Binary quadratic form 388
Brahmagupta's identity 320
Brouncker, William 314
Calendars 47 285
Carmichael function 187
Carmichael number 86
Ch'in Chiu-Shao 68
Chebyshev, Pavnuty 218
Chinese remainder theorem 46
Disquisitiones Arithmeticae (Gauss) 69
Divisibility tests 42
Division algorithm 7 359
Division algorithm for polynomials 103
divisors 7
Divisors, number of positive 12
Divisors, proper 10
Divisors, sum of positive 12
Eisenstein, Ferdinand 156
Elements (Euclid) 37
Euclid 37
Euclidean algorithm 14
Euclidean Algorithm, еxtended Euclidean Algorithm 15
| Euclidean quadratic field 368
Euler  -function 75 -function 75
Euler's criterion 73 129
Euler's theorem 76
Euler, Leonhard 99
Extended Euclidean algorithm 15
Factoring large numbers 347
Factoring Method, Legendre's 327
Factorization, prime 11
Fermat number 198
Fermat prime 198
Fermat's last theorem 224
Fermat, Pierre de 98
ind a index of a 164
Modulus 40
Multiple 7
Multiplicative function 13
Nonresidue, quadratic 128
Norm Gaussian 358
Norm in 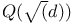 367 367
Number of positive divisors 12
Number of representations 228 235
ord a order of a 159
Order of an integer 159
Partial quotient 271
Pell's equation 314
Pell's Equation, 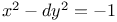 322 322
Pell's Equation, 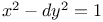 315 315
Pell's Equation, 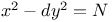 324 324
Pell's Equation, least positive solution 317
Perfect number 196
Period of a continued fraction 278
Periodic continued fraction 278
Polynomial congruence, root 101
Polynomial congruence, solution 101 102 106
Power residue 165
Prime 10
Prime, 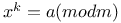 165 165
Prime, Gaussian 358
Sum of positive divisors 12
Sum of squares, four squares 233
Sum of squares, four squares, number of representations 235
Sum of squares, three squares 235
Sum of squares, two relatively prime squares 229
Sum of squares, two squares 228
Sum of squares, two squares, number of representations 229
Unique factorization theorem 11 361 369
Unit Gaussian 358
Unit of 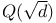 367 367
Waring's problem 236
Wilson's theorem 73
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



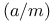 Jacobi symbol
Jacobi symbol 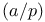 Legendre symbol
Legendre symbol 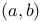 greatest common divisor
greatest common divisor 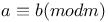 a congruent to b modulo m
a congruent to b modulo m 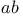 a does not divide b
a does not divide b 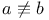 (mod m) a not congruent to b modulo m
(mod m) a not congruent to b modulo m 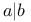 a divides b
a divides b 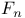 nth Fermat number
nth Fermat number 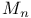 nth Mersenne number
nth Mersenne number 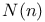 number of representations of n as a sum of two squares
number of representations of n as a sum of two squares ![$[a, b]$](/math_tex/bd4455e79810acc06e3d31c60fb8bfb282.gif) least common multiple
least common multiple ![$[x]$](/math_tex/7e1c4a3a07c941625c2f20c594cb9f7c82.gif) greatest integer not exceeding x
greatest integer not exceeding x  Euler
Euler  -function
-function 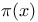 number of primes not exceeding x
number of primes not exceeding x  sum of positive divisors of n
sum of positive divisors of n 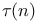 number of positive divisors of n
number of positive divisors of n