|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Heinonen J. — Lectures on Analysis on Metric Spaces |
|
|
 |
| Предметный указатель |
"Thick" families of curves 29 68
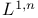 -extension property 65 -extension property 65
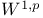 -extension domain 40 -extension domain 40
 -lemnia 96 -lemnia 96
(1, 1)-Poincare inequality 73 76
(1, n)-Poincare inequality, connection with n-Loewner condition 70
(1, p)-Poincare inequality 69
3-manifolds 120
4-manifold 98 121
Absolutely continuous on almost every line 38 40
Admissible functions 51
Admissible metrics 51
Ahlfors regular space 62 112
Antoine's necklace 116
Arc length parametrization 50
Ascoli's theorem 85
Assouad dimension 81 104 113 125
Assouad embedding theorem 98 112 121
Axiom of Choice 3
Banach space 8 99 120
Basic covering theorem 2 11
Besicovitch — Federer covering theorem 7 12
Bessel potentials 23
Bi-Lipschitz 8 71 78
Bi-Lipschitz embedding 99
Bi-Lipschitz embedding in Euclidean space 98 102 124
Bi-Lipschitz equivalence 110 113
bi-Lipschitz map 78 116
Borel regular 3
Bounded turning 120
Bourdon — Pajot space 67 75 99 123
Broad domain 66
Brownian motion 88
BV function 25 see
Calderon differentiability theorem 47
Cantor set 67 108 118 121
Cantor ternary set 60 62 88 92 114 121 122
Capacity 56 66
Carnot group 67 76 123
Carnot metric 67 76
Cauchy sequences 81
Chain condition 30
Chain condition in geodesic spaces 72
Characteristic function 11
Cheeger — Sobolev space 56
Coarea formula 24
Codifferential 16
Coloring 101 102
Compact-open topology 86
Complex dynamics 95 107
conformal 51 95
Conformal dimension 121
Conformal gauge 119
Conformal gauge of Cantor set, characterization of 121
Conformal gauge, flat 124
Conformal gauge, fractal 122
Conformal gauge, of one-dimensional spaces, characterization of 120
Conformal modulus 52
Conformal modulus of ring domains 52
Conformal modulus, conformal invariance of 51
Conformal modulus, historical remarks on 54
Continuum 59 64
Continuum, nondegenerate 59
Convolution 17 37
Covering 1
Covering dimension 81 see
Covering function 81
Curve 49
Directionally limited set 7
Dirichlet problem 108
Dirichlet spaces 56
Disjointed 2
distribution 14
Distribution function 12
Divergence 15
Doubling 3 98 118 119
Doubling measure 3 82 107
Doubling measure and quasisymmetrically thick sets 117
Doubling measure on quasimetric space 110
Doubling measure, deformation by 109 112
Doubling metric space 81—83
Doubling metric space, quasisymmetric invariance of 82
Egg yolk principle 93
Elliptic partial differential equations 108
Flat conformal gauge 124
Fractal conformal gauge 122
Frostman's lemma 62
Gauge, conformal 119
Gauge, metric 121
Gauge, topological 119
Geodesic 70 120
Geodesic space 31
Gromov boundary 120
Gromov hyperbolic space 120
H = W theorem 18 26 40
Hajlasz — Sobolev space 35 49 56
Hajlasz — Sobolev space, local versions of 41
Hajlasz — Sobolev space, Poincare inequality for 39
Hardy — Littlewood maximal function theorem 10 21 37
Harmonic measure 88 108
Hausdorff content 61 74
Hausdorff dimension 60 62 81 92 103 107 116
Hausdorff dimension of Loewner spaces 63
Hausdorff dimension, relation to topological dimension 62
Hausdorff dimension, ways to estimate 61
Hausdorff measure 60
Heisenberg group 8 67 76 99 123
Hilbert space 8 99
Hodge star operator 15
Hoelder continuous 89
Hoelder continuous function 18 44
Holomorphic motion 95 97
Homogeneous measure 103 107
Homogeneously dense 97
Hyperbolic geometry 88
Hyperbolic metric 96
Inner regular 3
Integrable 3
integral 3
Internal distance 66 95
Interpolation argument 12
Isometric embedding, in Banach spaces 99
Isoperimetric dimension 25
Isoperimetric inequality 24 49
Isoperimetric profile 25
John domain 66 95
Jones's Sobolev extension theorem 66 94
Julia set 88 96
Kirzsbraun's theorem 44
Klee trick 89
Kleinian group 89 95 107
Koebe distortion theorem 93
Kuratowski embedding 99
Laakso space 67 75 99 123
Lebesgue point 47
Lebesgue's Differentiation Theorem 4 10 12
Length 50
length function 50
Length space 71
Lie group 67
Limit set 88 96
Line integral 50
Linear local connectivity 64—67 94 95
Linear local connectivity of Loewner spaces 64
Lipschitz function 40 43
Lipschitz function, differentiability almost everywhere of 47
Lipschitz function, extensions of 44 48
Local Sobolev space 14
Locally integrable 5
| Locally quasiconvex 57
Locally rectifiable 50
Loewner function 59 68 94
Loewner function, asymptotics of 64
Loewner space 59 63 65 67 73 75 122
Loewner space, example of 60 65
Loewner space, Hausdorff dimension of 63
Loewner space, linear local commectivity of 64
Loewner space, quasiconvexity of 64
Lower semicontinuous 45
Lusin theorem for Sobolev functions 40
Mandelbrot set 96
Mapping problem 95 97
Mass distribution principle 104 106
Maximal function 10 74
Mazur's theorem 36
McShane extension theorem 43
Mean value 5 10
Measure 3
Metric covering dimension 81 see
Metric doubling measure 113 118
Metric doubling measure and uniform disconnectivity 115
Metric gauge 121
Minimal upper gradient 58
Modulus 50
Modulus of continuity 45
Net 101 104
Newtonian spaces 56
Newtonian spaces, reflexivity of 56
Normal family 85
Normed space 7
Orthonormal basis 100
Outer regular 3
p-capacity 56
p-capacity, equality with p-modulus 57
p-modulus 50
p-modulus of ring domains 53
Pansu differentiability theorem 99
Pencil of curves 30
Poincare inequality 17 28 39 56
Poincare inequality for Lipschitz functions 75
Poincare inequality for measurable functions 75
Poincare inequality, self-improvement and 30
Porous 116
Potential estimate 20
Power quasisymmetric 89
Proper 58 70 86 120
Pullback measure 107 113
QED domain 66
Quasiconformal map 52
Quasiconformal map, local quasisymmetry of 92
Quasiconvex 57 66 70
Quasiconvex of Loewner spaces 64
Quasidisks 95
Quasiextremal distance domain 66
Quasimetric 109 118
Quasimetric, determined by doubling measures 112
Quasimoebius map 94 96
Quasiregular maps 58
Quasisymmetric 78 112 113
Quasisymmetric map 107
Quasisymmetric map and Cauchy sequences 81
Quasisymmetric map and holomorphic motions 95
Quasisymmetric map in Euclidean domains 92
Quasisymmetric map on quasimetric space 110
Quasisymmetric map, absolute continuity of 117
Quasisymmetric map, basic properties of 79
Quasisymmetric map, compactness properties of 85
Quasisymmetric map, equicontinuity of 85
Quasisymmetric map, extension of 89
Quasisymmetric map, singular 107
Quasisymmetrically embeddable, in Euclidean space 98
Quasisymmetrically thick 108 117
Quasiultrametric 110
Rademacher theorem 47 48
Rademacher — Stepanoff theorem 47
Radon measure 7 12 17
Rational numbers 103
Real hyperbolic space 65
Rectifiable 50
Rectifiable curves 60
Reflexive Banach space 56
Regular map 102
Regular space 62
Removable set for Sobolev functions 40
Removable set for Sobolev spaces 58
Restricted maximal function 11 69
Ricci curvature, nonnegative 75
Riemann sphere 107
Riemann surface 107
Riemannian manifold 8 15 51 75 92
Riesz potential 20 34 69 74
Schwartz lemma 96
Self-improvement 30
Sierpinski carpet 125
Singular integral operators 102
Slit disk 40
Slodkowski's theorem 96
Snowflake 110 121
Snowflaked metric space 78 98
Sobolev conjugate 18
Sobolev embedding theorem 18 47 65
Sobolev function, differentiability almost everywhere of 47
Sobolev function, Hajlasz inequality for 34
Sobolev inequalities 18
Sobolev inequalities, connection with isoperimetric inequalities 24
Sobolev space 15
Sobolev space of differential forms 15
Sobolev space, Hajlasz formulation 36
Sobolev — Poincare inequality 49
Starlike domain 40
Stokes theorem 16
Sub-Riemannian geometry 26
Subharmonic functions 88
Subinvariance principle 97
Teichmueller spaces 87
Tensor product 100
Topological dimension 62
Topological gauge 119
Topological gauge, dimension of 125
Transfinite induction 101
Trudinger's inequality 18
Twice-punctured plane 96
Ultrametric 110 114
Uniform convexity 36
Uniform domain 66 94 95 125
Uniform metric dimension 81
Uniformly continuous function 45
Uniformly disconnected 118
Uniformly disconnected spaces 114
Uniformly disconnected spaces, quasisymmetric invariance of 114
Uniformly perfect 88 103 112 121
Uniformly perfect, quasisymmetric invariance of 89
Uniformly perfect, quasisymmetry and 89
Upper gradient 55
Urysohn's theorem 119
Vitali covering theorem 3
Vitali space 6
Vitali — Caratheodory theorem 51
Vol'berg — Konyagin theorem 104
Volume growth 25 61 64 65
Weak (1, p)-Poincare inequality 68
Weak differential 16
Weak gradient 15 47 65
Weak partial derivative 14
Weak quasisymmetry 83
Weakly quasisymmetric 79
Well-ordering principle 101
Zorn's lemma 2 101
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



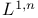 -extension property
-extension property 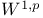 -extension domain
-extension domain  -lemnia
-lemnia