
Обсудите книгу на
Нашли опечатку?
Выделите ее мышкой и нажмите Ctrl+Enter
|
Название: Topological quantum field theories and geometry of loop spaces
Авторы: Feher L. (ed.), Stipsicz A. (ed.), Szenthe J. (ed.)
Язык: 
Рубрика: Физика/Квантовая теория поля/Квантовая гравитация/
Статус предметного указателя: Готов указатель с номерами страниц
ed2k:
Год издания: 1992
Количество страниц: 112
Добавлена в каталог: 21.08.2005
Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
|
 |
|
О проекте
|
|
О проекте



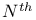 -Jones polynomial
-Jones polynomial 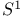 -manifold
-manifold 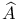 polynomial
polynomial 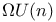
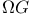
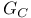 -bundles
-bundles