|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Steele M.J. — Stochastic Calculus and Financial Applications |
|
|
 |
| Предметный указатель |
 space 18 space 18
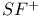 249 249
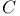 inlar, E. vi inlar, E. vi
 252 252
 problem 159 problem 159
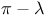 theorem 208 theorem 208
 -field 43 -field 43
Adapted 50
Admissibility 252
Admissible strategies 252
Admissible strategies, uniqueness 254
Alternative fields 106
American option 244 290
Analysis and synthesis 111
Approximation, finite time set 209
Approximation, in 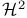 90 90
Approximation, operator 90
Approximation, theorem 90
Arbitrage 153
Arbitrage, risk-free bond 249
Artificial measure method 44
Asian options 258
Augmented filtration 50
Axler, S. 288
Bachelier, L. 29
Bass, R. 287 290
Baxter 290
Benedito, J.J. 286
Bessel's inequality 281
Binomial arbitrage 155
Binomial arbitrage, reexamination 233
Black - Scholes formula 158
Black - Scholes formula, via martingales 241
Black - Scholes model 156
Black - Scholes PDE, and Feynman - Kac representation 274
Black - Scholes PDE, and Feynman-Kac 271
Black - Scholes PDE, CAPM argument 162
Black - Scholes PDE, general drift 274
Black - Scholes PDE, hedged portfolio argument 160
Black - Scholes PDE, how to solve 182
Black - Scholes PDE, simplification 186
Black - Scholes PDE, uniqueness of solution 187
Borel - Cantelli Lemma 27 279
Borel field 60
Box algebra 124
Box calculus 124
Box calculus, and chain rule 123
Brown, Robert 120
Brownian bridge 41
Brownian bridge, as It integral 141 integral 141
Brownian bridge, construction 41
Brownian bridge, SDE 140
Brownian motion, covariance function 34
Brownian motion, definition 29
Brownian motion, density of maximum 68
Brownian motion, geometric 137 138
Brownian motion, H lder continuity 63 lder continuity 63
Brownian motion, hitting time 56
Brownian motion, killed 264
Brownian motion, L vy's characterization 204 vy's characterization 204
Brownian motion, not differentiable 63
Brownian motion, planar 120
Brownian motion, recurrence in 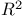 122 122
Brownian motion, ruin probability 55
Brownian motion, scaling and inversion laws 40
Brownian motion, time inversion 59
Brownian motion, wavelet representation 36
Brownian motion, with drift 118
Brownian motion, writes your name 229
Brownian paths, functions of 216
Burchfield, J.D. 289
Calculations, organization of 186
Campbell, J.Y. 288
CAPM 162
Capturing the past 191
Carslaw, H.S. 289
casinos 7 285
Cauchy sequence 280
Central limit theorem 279
Central limit theorem, via embedding 78
Characteristic function 30
Chebyshev's inequality 279
Chung, K.L. vi 287
Churchill, W. 66
Coefficient matching 137 157
Coffin state 264
Coin tossing, unfair 5
Complete metric space 280
Complete orthonormal sequence 33 283
Completeness 252
Completeness, of 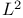 280 280
Completeness, of model 252
Conditional expectation 278
Conditional expectation, as contraction 48
Conditional expectation, continuity of 201
Conditional expectation, definition 45
Conditional expectation, existence 46
Conditional expectation, uniform integrability 48
Conservation law 170
Constitutive law 170
Contingent claim 252
Covariance and independence 41
Covariance function 32
Covariance function, calculation 38
Cox, J. 290
Credit constraint 248
Credit constraint supermartingale 248
Dambis, D.E. 290
DeMoivre - Laplace approximation 72
Density argument 200 210
Derivative security 155
Dewynne, J. 289
Difference operator 4
Diffusion equation 169
Diffusion equation, derivation 171
Diffusion equation, nonuniqueness example 178
Diffusion equation, solution methods 172
Diffusion equation, uniqueness question 178
Diffusion Equation, Uniqueness Theorem 181
Diffusion equation, with constant coefficients 183
Discounting 235
Dominated Convergence Theorem 278
Dominated convergence theorem, conditional 279
Donsker's invariance principle 71
Doob's decomposition 28
Doob's inequalities 19
Doob's stopping time theorem, local martingales 105
Drift removal 222
Drift swapping 224
Dubins, L. 287 290
Dudley's representation theorem 194
Dudley's representation theorem, nonuniqueness 196
Dudley, R.M. 287 290
Duffie, D. vi 290
Durrett, R. 287 290
Edgar, G.A. 290
Einstein, A. 29
Embedding theorem 76
Epstein, R.A. 285
Equivalent martingale measure 236
Equivalent martingale measure, existence and uniqueness 241
Equivalent martingale measure, uniqueness 240
Equivalent measures 220 236
Euler, L. 289
Existence and uniqueness theorem for SDEs 142
Exponential local martingales 224
Exponential martingales 225
Fatou's lemma 278
Feller, W. 285
Feynman - Kac formula 263
| Feynman - Kac representation and Black - Scholes PDE 271
Feynman - Kac representation for diffusions 270
Feynman - Kac representation theorem 265
Filtration 50
Filtration, standard Brownian 50
Financial frictions 153
First step analysis 1
Forward contracts 154
Fourier transform method 172
Frazier, M.W. 286
Freedman, D. vi
Friedman, B. 287
Fristedt, B. 291
Gaussian miracle 30
Gaussian process 32
Gaussian tail bounds 42
General Case, U.S. Army 291
Generating functions 7
Girsanov theorem, for standard processes 223
Girsanov theorem, simplest 219
Girsanov theory 213
Girsanov, I.V. 213
Gray, L. 291
Gronwall's lemma 150
H lder continuity 62 lder continuity 62
H lder inequality 21 lder inequality 21
H lder inequality, applied to Novikov 231 lder inequality, applied to Novikov 231
H lder inequality, or Roger inequality 287 lder inequality, or Roger inequality 287
H lder inequality, proof via Jensen 44 lder inequality, proof via Jensen 44
Harmonic functions 120
Harrison, J.M. vi 290 291
Heat kernel 174
Heat operator 174
Hilbert space 210 280
Hitting time, biased random walk 6
Hitting time, Brownian motion 56
Hitting time, density 69
Hitting time, simple random walk 4
Hitting time, sloping line 219
Howison, S. 289
Ikeda, N. 287
Importance sampling 213 290
Incompleteness example 260
Independence and covariance 41
Induction 229 289
Informative increments proposition 193
Integral sign 85
Interest rate (two-way) 154
Invariance principle 71
It formula, location and time 116 formula, location and time 116
It formula, simplest case 111 formula, simplest case 111
It formula, vector version 121 formula, vector version 121
It integral, integral, 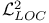 95 95
It integral, as Gaussian process 101 integral, as Gaussian process 101
It integral, as martingale 83 integral, as martingale 83
It integral, as process 82 integral, as process 82
It integral, definition 79 integral, definition 79
It integral, pathwise interpretation 87 integral, pathwise interpretation 87
It isometry 80 85 isometry 80 85
It isometry, conditional 82 131 isometry, conditional 82 131
It isometry, counterexample in isometry, counterexample in 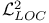 211 211
It isometry, on isometry, on ![$\mathcal{H}^{2}[0,T]$](/math_tex/d74e13d286b550195d04bec60a040e3582.gif) 82 82
It , K. 286 288 , K. 286 288
Jaeger, J.C. 289
Jensen's inequality 18 287
John, F. 289
K rner, T.W. 285 289 rner, T.W. 285 289
Karatzas, I. vi 286-288 290
Kloeden, P.E. 288
Kreps, D. 290
L vy - Bachelier formula 219 230 vy - Bachelier formula 219 230
L vy's Arcsin Law 267 vy's Arcsin Law 267
L vy's modulus of continuity theorem 65 vy's modulus of continuity theorem 65
L vy, P. 287 vy, P. 287
Landau, E. 286
Lebesgue integral 277
Leibniz 85
Leveraging an abstraction 44
Li, W.V. vi 288
Lin, C.C. 285 289
Lipster, R.S. 290
Lo, A.W. vi 288
localization 96 114 225
Localization, discrete time example 23
Look-back options 258
Looking back 2 57 118 119 138 142 186 201 229
MacKinlay, A.C. 288
Market price of risk 239
Markov's inequality 279
Martingale representation theorem 197
Martingale representation theorem, in  211 211
Martingale transform 13
Martingale,  -bounded 24 -bounded 24
Martingale,  27 27
Martingale, continuous 50
Martingale, convergence theorem 22
Martingale, creation of 221
Martingale, local 103
Martingale, PDE condition 116 121
Martingale, with respect to a sequence 11
Matching coefficients in product process 139
Maximal inequality, Doob's 19
Maximal inequality, Doob's in continuous-time 52
Maximal sequence 19
Maximum principle 179
Maximum principle, harmonic functions 189
Maximum principle, parabolic 179
Maximum principle, via integral representation 189
McKean, H.P. 286 287
Mean shifting identity 214
mesh 128
Meyer, Y. 286 287
Mice, diffusion of 169
Modes of convergence 58
Monotone class theorem 209
Monotone Convergence Theorem 278
Monte Carlo 66
Monte Carlo, improved 214
Multivariate Gaussian 30 41
Musiela 290
Neveu, J. 286
Newton's Binomial Theorem 8
No early exercise condition 245
Normal distribution, in 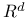 30 30
Novikov condition 225 290
Novikov condition, lazy man's 231
Novikov condition, sharpness 230
Numerical calculation and intuition 7
Occupation time of an interval 274
Omnia 85
Ornstein - Uhlenbeck process 138
Ornstein - Uhlenbeck process, SDE 138
Ornstein - Uhlenbeck process, solving the SDE 140
Orthonormal sequence 281
P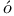 lya's question 77 lya's question 77
P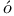 lya, G. 2 77 246 286 289 291 lya, G. 2 77 246 286 289 291
Parallelogram law 283
Parseval's identity 34 282
Persistence of identity 89 98
Phelan, M. vi
Pitman, J. vi
Platen, E. 288
Pliska, S.R. 290
Polarization trick 134
Portfolio properties 243
Portfolio weights 237 243
Portfolio weights, abstract to concrete 261
Power series 7 225 226
Pozdnyakov's example 260
Pozdnyakov, V. vi 260
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 space
space 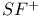
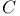 inlar, E.
inlar, E. 
 problem
problem 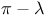 theorem
theorem  -field
-field 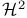
 integral
integral  lder continuity
lder continuity  vy's characterization
vy's characterization 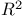
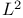
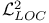
![$\mathcal{H}^{2}[0,T]$](/math_tex/d74e13d286b550195d04bec60a040e3582.gif)

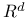
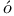 lya's question
lya's question