Авторизация
Поиск по указателям
Babin A.V., Vishik M.I. — Attractors of Evolution Equations
Обсудите книгу на научном форуме Нашли опечатку?
Название: Attractors of Evolution EquationsАвторы: Babin A.V., Vishik M.I. Аннотация: Problems, ideas and notions from the theory of finite-dimensional dynamical systems have penetrated deeply into the theory of infinite-dimensional systems and partial differential equations. From the standpoint of the theory of the dynamical systems, many scientists have investigated the evolutionary equations of mathematical physics. Such equations include the Navier-Stokes system, magneto-hydrodynamics equations, reaction-diffusion equations, and damped semilinear wave equations. Due to the recent efforts of many mathematicians, it has been established that the attractor of the Navier-Stokes system, which attracts (in an appropriate functional space) as t - infin; all trajectories of this system, is a compact finite-dimensional (in the sense of Hausdorff) set. Upper and lower bounds (in terms of the Reynolds number) for the dimension of the attractor were found. These results for the Navier-Stokes system have stimulated investigations of attractors of other equations of mathematical physics. For certain problems, in particular for reaction-diffusion systems and nonlinear damped wave equations, mathematicians have established the existence of the attractors and their basic properties; furthermore, they proved that, as t - +infin;, an infinite-dimensional dynamics described by these equations and systems uniformly approaches a finite-dimensional dynamics on the attractor U, which, in the case being considered, is the union of smooth manifolds. This book is devoted to these and several other topics related to the behaviour as t - infin; of solutions for evolutionary equations.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1992Количество страниц: 532Добавлена в каталог: 13.02.2010Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
15 251 282 436 160 13 14 157 157 31 31 160 163 343 162 186 124 201 202 221 202 (type of set) 301 281 220 158 217 217 157 147 319 322 201 480 13 233 242 230 242 318 *-weakly convergent sequence 20 Absorbing set 32 Absorbing set, uniformly 400 Almost stable semigroup 201 Asymptotics, of 322 Asymptotics, of 251 258 259 260 392 Asymptotics, of 434 see Asymptotics, of 279 281 375 382 391 Attracting set 118 Attracting set, uniformly 424 Attraction 117 Attraction, exponential 4 05 Attractor 21 119 Attractor, point-attracting 163 Attractor, regular 270 Bair's Theorem 301 Boussinesg equation 502 c.l.t. 436 452 453 457 460 470 474 Class 223 Class 223 233 Class 241 Class 241 Class 241 Class 241 Class 223 233 Closure 21 Combined limit trajectory 436 see Compact set 21 Continuous operator 33 Continuous operator, uniformly 33 Courant's Minimax, Principle 3 20 Critical point of a curve 335 Critical value 301 Damped hyperbolic equation 103 131 165 171 214 259 262 378 416 460 500 Damped hyperbolic system 148 170 216 Damped wave equation see “Damped hyperbolic equation” Derivative in the sense of distributions 19 Differential inequalities 23 Dimension (Hausdorff) 479 Dirichlet boundary condition 64 Dissipation integral 172 180 Dist 137 Distance 137 Distance, symmetric 137 Ellipticity condition 90 Embedding 17 Equilibrium point 160 F.-d.c.t. 282 Finite-dimensional, combined trajectory 28 2 Fourier coefficients 15 Frechet differentiable operators 341 Frechet differential 341 Fredholm operator, differentiable 301 313 Fredholm operator, linear 300 Gagliardo — Nirenberg inequality 18 Galerkin system 39 Gel'fand theorem 204 Green function 3 20 Gronwall inequality 23 Group 29 148 Hartman — Grobman theorem 261 Hausdorff dimension 479 Hausdorff measure 479 Hoelder condition 222 Hoelder continuous function 14 Hoelder's inequality 23 Hyperbolic equation see “Damped hyperbolic equation” Hyperbolic point 240 245 Implicit function theorem 346 Index, of a Fredgolm operator 300 Index, of a linear semigroup 205 Index, of instability 318 337 Inflection, point of 337 Inhomogenious variation equation 345 Injectivity 148 Instability index 337 Interpolation inequality 18 Invariance, inverse 118 Invariance, strict 119 Invariant, manifold, analytic 245 Invariant, manifold, of class 223 Invariant, set 159 Invariant, trajectory 157 Linearization, 262 Linearization, analytical 266 268 Linearization, continuous 261 Linearization, global 262 268 Linearization, smooth 265 Liouville formula 486 Local unstable set 217 Locally invariant set 241 Lyapunov function 159 Lyapunov stability modulo attractor 120 Magnetohydrodynamics equations 503 Manifold, 223 241 249 Manifold, 249 Manifold, 233 241 Manifold, local invariant 249 Manifold, of class 223 Massive 301 Maximal attractor 119 Minimax principle 320 Monotone parabolic equation 34 47 127 181 189 410 Monotonicity condition 179 182 Monotonicity condition, strong 179 Morse — Smale system 295 Navier — Stokes system, three-dimensional 392 Navier — Stokes system, two-dimensional 76 129 189 260 330 383 412 413 414 492 Neighbourhood, 241 Neighbourhood, 241 Neighbourhood, 241 Neighbourhood, 117 Neighbourhood, of a set 117 Neumann boundary condition 64 Nonlinear theory of shells, system 170 176 Norm, 14 Norm, 14 Norm, 14 Norm, 15 Norm, 15 Norm, 15 Norm, 15 Norm, 15 Norm, in: 14 Norm, in: 15 Norm, in: 222 Norm, in: 15 Norm, in: 15 Operators 222 Orbit 157 Passing neighbourhoods, in order reverse to the numeration 435 Poincare theorem 266 Precompact 21 Pressing exponential 218 Proper mapping 298 Quasidifferentiable, mapping 479 Quasidifferentiable, mapping, uniformly 479 Quasidifferential 480 Quasilinear operators 299 309 Quasilinear parabolic, equations 90 130 153 163 386 452 498 Reaction-diffusion system 63 168 208 258 368 456 487 498 Reaction-diffusion system, steady-state solutions 327 Regular value 301 Resonances 266 Rest-untending points 186 Riesz projections 326 Sard — Smale theorem 302 Scalar product in 15 Semigroup 29 Semigroup identity 29 Semigroup, bounded 31 Semigroup, bounded, for 31 Semigroup, bounded, for 31 Semigroup, bounded, uniformly for finite t 32 Semigroup, bounded, uniformly in t 31 Semigroup, close to linear 248 354 Semigroup, continuous 3 3 Semigroup, continuous, uniformly 33 Semigroup, linear 194 201 205 206 209 Semilinear operators 299 Semiorbit 157 Semitrajectory 157 Semitrajectory, negative 147 Shmuljan — Eberlane theorem 21 Singularly perturbed equations 416 465 474 Sobolev's embedding theorems 17 Sobolev's space, 16 Sobolev's space, 15 Sobolev's space, 15 Spaces, 14 Spaces, 14 Spaces, 16 Spaces, 16 Spaces, 14 Spaces, 15 Spaces, 19 Spaces, 14 Spaces, 19 Spaces, 22 Spaces, 16 Spaces, 15 Spaces, 16 Spaces, 22 Spaces, 15 Spaces, 14 15 Spaces, 19 Spaces, 19 Spaces, 16 Spaces, 15 Spaces, 15 Spaces, L 342 Spaces, L' 343 Stability 120 Stability, Lyapunov modulo attractor 120 Stable set 158 Steady-state solutions 297 Stretch exponential 219 Subspace, corresponding to 202 Subspace, invariant 203 Subspace, stable 204 Subspace, unstable 204 Tikhonov's lemma 154 Time of arrival 283 Torus 13 Trace 480 Trajectory, bounded 157 Trajectory, invariant 157 Turning point 336 Uniformly absorbing set 400 Uniformly continuous semigroup 33 Uniformly differentiable operator 341 Uniformly quasidifferentiable mapping 479 Unstable set 157 217 Upper semicontinuous dependence 402 Value, critical 301 Value, regular 301 Variation equation inhomogenious 345 Viscoelasticity, equation 169 Viscoelasticity, linearized equation 2 Weak topology 21 Weakly continuous trajectory 21 weakly convergent sequence 20 Young's inequality 22 [L.S.U.] 91
Реклама
 |
|
О проекте
|
|
О проекте



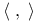
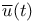
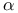 -limit set
-limit set 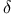 u
u 
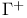





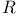

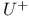
 -limit set
-limit set 
 and
and 

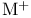

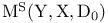
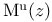


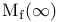

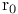



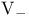

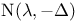
 spectral
spectral 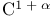

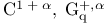
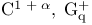
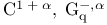
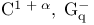

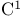

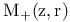
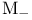




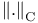
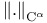
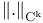
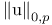


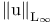


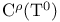
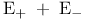

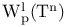
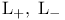
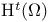


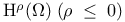
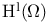 (integer 1)
(integer 1) 




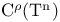
![${\rm C}^{\rm k}([0,\;T];\;E)$](/math_tex/27f4f1baf96dd166e2323fb9aa09566482.gif)
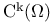

![${\rm C}^{\rm t,2t}([0,T]\;\times\;{\overline{\Omega}})$](/math_tex/34e50984563172939448e1b3cc71996782.gif)


![${\rm H}^{\rm t,2t}([0,T]\;\times\;{\overline{\Omega}})$](/math_tex/f1c054f66d41d67f206c1fe9b494b0a882.gif)



![${\rm L}_{\rm p}([0,\;T];\;E)$](/math_tex/a8f0380d21b043de8092d5b5f56a6e0482.gif)

