|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Andrews G.E. — Number Theory |
|
|
 |
| Предметный указатель |
"Even prime" 28
Abel's lemma 190—191 195
Absolute convergence, for infinite products 217
Additivity 139
Alder, H.L. 229—231
Algebra, abstract v
Algorithm, Euclidean 16
Andrews, G.E. 227 229—231
Arithmetic functions 75—92
Arithmetic functions, multiplicative 85—86 88
Arithmetic mean 92
Ayoub, R. 230—231
Base 8 10
Basis representation 3—11
Basis representation theorem 8—11 26 227
Belongs to the exponent h 93
Bertrand's postulate 111
Binary notation 8
Binomial coefficient 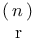 32 32
Binomial series 42
Binomial theorem 35
Birkhoff, G. 55
Bromwich, T.J.I'A. 229 231
Cancellation law 51
Card shuffling 56—57
Card shuffling, historical note 227
Carmichael's conjecture 82
Carmichael, R.D. 82 227 231
Casting out nines 64
Catalan number (Theorem 3—6) 41
Cauchy sequence 218
Chebyshev, P. see "Tchebychev P."
Chinese remainder theorem 66—71 228
Circle problem see "Gauss's Circle Problem"
Combination 32
Combinatorial analysis see "Combinatorics"
Combinatorics v 227
Common denominator 22
Complementary divisors 243
Complete residue system 52—53
Complex conjugate 143
Complex number 143
Complex number, absolute value of 143
Computers and binary numbers 10
Computers and numerical examples v 44—48
Computers in number theory 30 227
Congruences v 1
Congruences, definition of 49
Congruences, fundamentals of 49—57
Congruences, linear 58—61
Congruences, mutually incongruent solutions of 59—60
Congruences, polynomial 71—74
Congruences, quadratic 113
Congruences, solving 58—74
Conjugate partitions 151
Convergence absolute 223
Convergence absolute of double series 223
Convergence absolute of products 217
Convergence by columns 221
Convergence by rows 221
coordinates 23
de La Vallee Poussin, C. 100
Decimal system 8
Derivative, 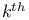 73 73
Dickson, L.E. 227—229 231
Diophantine equations 146—147
Diophantine equations, linear 23—26 58—59
Diophantus of Alexandria 141
Dirichlet's divisor problem 207—210 229
divides 15
Divisibility 1 15—23
Division lemma see "Euclid's division lemma"
Divisor 15
Divisor function and Dirichlet's Divisor Problem 207—210 229
Divisor function and geometric number theory 199
Divisor function and Moebius pairs 89—90
Divisor function and numerical table 47
Divisor function and sum of divisors 92
Divisor function as arithmetic function 1 75
Divisor function as multiplicative function 85—86
Divisor function, average value of 201
Divisor function, formulae for 82—85
Divisor function, historical note 228
Divisor function, table of values 77
Divisor problem see "Dirichlet's Divisor Problem"
Divisor, common 15
Divisor, greatest common 15
Double series 221—225
Double series, absolute convergence of 223
Double series, convergence of 223
Empty partition 149 181 192
Empty product 184
Empty set 33
Equivalence relation 50
Erdoes, P. 81 100
Euclid 100
Euclid's division lemma 12—15
Euclidean algorithm 16
Euler's  -function and Moebius pairs 89—91 -function and Moebius pairs 89—91
Euler's  -function and numerical table 48 -function and numerical table 48
Euler's  -function as multiplicative function 85—86 -function as multiplicative function 85—86
Euler's  -function, combinatorial study of 75—82 -function, combinatorial study of 75—82
Euler's  -function, definition of 54 -function, definition of 54
Euler's  -function, historical note 228 -function, historical note 228
Euler's  -function, table of values 77 -function, table of values 77
Euler's criterion 115—117
Euler's partition theorem 150 154—156 164—165
Euler's partition theorem, searching for 155—156
Euler's pentagonal number theorem see "Pentagonal Number Theorem"
Euler's theorem 62
Euler, L. 45 111 118 149—150 175
Exponent, to which a belongs 93
Factorial 32
Factorizations into primes, table of 26
Faro shuffle, modified perfect 56—57
Fermat numbers 65—66 71 104
Fermat's conjecture 147 229
Fermat's last theorem 147
Fermat's little theorem as a congruence 49
Fermat's little theorem, combinatorial proof 36—38
Fermat's little theorem, historical notes 227 228
Fermat's little theorem, proof by congruences 61—66
Fermat, P. 36 147
Fibonacci numbers 6—7 35 44
Fibonacci numbers, generalized 23
Fields, finite v
Flow chart 45—46
Flow diagram 45—46
Four-square problem see "Sums of four squares"
Fractional part of x 207
Fundamental Theorem of Arithmetic v 12—29
Gauss's Circle Problem 201—207 229
Gauss's lemma 119
Gauss, C.F. 49 100 113 118—120
General combinatorial principle 31
Generating functions 30 40—44
Generating functions for 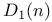 163—164 163—164
Generating functions for 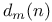 163 163
Generating functions for 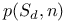 162—163 162—163
Generating functions for  165 165
Generating functions for 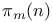 160—161 160—161
Generating functions for p(n) 162
Generating functions for partitions vi 160—174
Generating functions for the sequence A 40
Generating functions, applications of 164—167
Generating functions, infinite products as 160—167
Geometric mean 92
Geometric series and generating functions 41
Geometric series and partitions 161
Geometric series and primes 102
| Geometric series, finite (Theorem 1—2) 5
Geometry, analytic 23 199
Geometry, of numbers 201
Gerstenhaber, M. 118
Gillies, D. 44 112
Goldbach's conjecture 81 85 111
Goldbach, C. 81 111
Golomb, S.W. 227 231
Graphical representation 150—153
Greatest integer function 90—91 101 103—104 207
Grosswald, E. 228 230—231
Group 93
Group, cyclic 93
Group, finite v
Hadamard, J. 100
Hardy, G.H. 147 149—150 176 229 230—231
Heaslet, M.A. 227 232
Heine's theorem (Exercise 3) 173
Hilbert, D. 147
Ideal see "Integral ideal"
INDEX 96
Induction hypothesis 5
Inequality of the Geometric and Arithmetic Means 92
Infinite products 160 215—220 229
Infinite products, convergence of 215—219
Infinite products, divergence of 160
Infinite products, identities 167—174
Infinite products, partial products of 160
Infinite series 215—220 229 see "Geometric
Infinite series, convergence of 215
Infinite series, identities 167—174
Infinite series, MacLaurin series 43 219
Infinite series, Taylor series 43 73
Integral ideal 14
Integral part of x see "Greatest integer function"
Integral test 209 226
Introductio in Analysin Infinitorum 149 175
Inverse modulo c 60
Jacobi symbol 118 124
Jacobi's triple product identity 169—172 176—177 229
Jacobsthal sums, S(m) 135—138 228
Johnson, P.B. 227 231
Knopp, M.I. 230—231
Knuth, D.E. 227 232
l'Hospital's rule 214
Lagniappe 141
Lagrange's theorem 72
Lagrange's theorem and primitive roots 97
Lagrange's theorem, historical note 228
Lagrange, J. 72 144
Landau, E. 230 232
Lattice points 23 121 201—210
Least common multiple 22
Least residue 119
Least-integer principle 14 145
Legendre symbol 117—118
Legendre, A. 118
Lehmer, D.H. 228 232
Leibnitz, G.W. 38
LeVeque, W.J. 230 232
Linear combination, integral 18
Linear Diophantine equation see "Diophantine equation"
Littlewood, J.E. 147
Lucas number 7
MacLane, S. 55
Maclaurin series 43
MacLaurin series, for infinite products 219—220
MacMahon, P.A. 176
Mamangakis, S.E. 228 232
Mathematical induction 3—8
Mathematical induction, principle of 4 14
Menon, P.K. 229 232
Mersenne primes see "Primes"
Mersenne, M. 112
Moebius function and Moebius inversion formula 86—91
Moebius function as arithmetic function 75
Moebius function as multiplicative function 85—86
Moebius function, definition of 77
Moebius function, historical note 228
Moebius pair 88
Multiple, least common 22
Multiplicative functions see "Arithmetic functions"
Multiplicativity 1
Nines, casting out 64
Number theory, additive vi 139
Number theory, algebraic 230
Number theory, combinatorial 30—44
Number theory, computational 44—48
Number theory, elementary 230
Number theory, geometric 199
Number theory, multiplicative 1
Number-theoretic functions see "Arithmetic functions"
o-notation 205
p-Gons, regular stellated 39
p-Gons, stellated 38
Partial product 160
Partition function 149
Partition function, generating function for 162
Partition generating functions 160—174 see
Partition identities 150 175—198 229
Partition identities, searching for 155—159 see "Schur's
Partitions vi 230
Partitions, conjugate 151
Partitions, definition of 149
Partitions, elementary theory of 149—159
Partitions, empty 149 181 192
Partitions, generating functions 160—174
Partitions, self-conjugate 153
Pentagonal number theorem 175—178
Pentagonal numbers 177
Perfect numbers 45 85
Perfect numbers and Mersenne primes 112
Perfect numbers, even 45
Perfect numbers, odd 45
Permutation 32
Phi-function see "Euler's  -function" -function"
Pollard, H. 230 232
POLYGONS 38
Polynomial 72
Polynomial with integral coefficients 72
Polynomial, degree of 72
Polynomial, monic 74
Polynomial, reducible 74
Prime function, 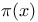 100—111 228 100—111 228
Prime number theorem 100
PRIMES 100—112
Primes and computers 44
Primes and fundamental theorem of arithmetic 26—29
Primes and multiplicativity 1
Primes and numerical table 47
Primes, definition of 20
Primes, historical note 228
Primes, Mersenne 44 112
Primitive roots 93—99 228
Primitive roots, definition of 94
Primitive roots, modulo p 97—99
Products see "Infinite products"
Pseudo-primes (Exercise 19) 65
Quadratic congruences 113
Quadratic nonresidue 128
Quadratic reciprocity law 113 118—127 228
Quadratic Reciprocity Law, applications of 125—127
Quadratic Reciprocity Law, statement of (Theorem 9—4) 120
Quadratic residues 47 115—127 228
Quadratic residues, consecutive pairs 128—133
Quadratic residues, consecutive triples 133—138
Quadratic residues, definition of 115
Quadratic residues, distribution of 128—138
r-Combination see "Combination"
r-Permutation see "Permutation"
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



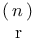
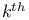
 -function and Moebius pairs
-function and Moebius pairs