|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Amorόs J., Burger M., Corlette K. Ч Fundamental Groups of Compact Kahler Manifolds |
|
|
 |
| ѕредметный указатель |
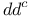 lemma 33 131 lemma 33 131
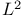 -cohomology 8 47Ч63 -cohomology 8 47Ч63
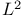 -cohomology, exact 48 -cohomology, exact 48
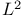 -cohomology, reduced 48 -cohomology, reduced 48
1-formal space 34 36Ч37
1-minimal model 29Ч32 37 41
Albanese, dimension 23
Albanese, image 23 40Ч43
Albanese, map 3 22Ч25 40Ч43
Albanese, variety 22Ч23 41
Betti moduli space 92Ч94
Bochner formula see УSiu Ч Sampson theoremФ
Bounded geometry 48 50 53Ч63
Castelnuovo Ч de Franchis 2Ч3 24Ч25 28 43 61 63 90
Cheeger Ч Chern Ч Simons classes 106
Commutative differential graded algebra (CDGA) 30Ч32 35Ч37
Commutative differential graded algebra (CDGA), dual Lie algebra of 32
Commutative differential graded algebra (CDGA), quasi-isomorphism of 30
Commutative differential graded algebra (CDGA), weak equivalence of 30 32
Compact complex surface 4Ч5 10Ч16 25 28
de Rham fundamental group 29Ч46 123
de Rham fundamental group, 2-step nilpotent 38
Eilenberg Ч Mac Lane space 2Ч3 8 13 21 23 33Ч34 82Ч83
Ends of groups 8Ч9 12Ч13 47Ч51 60Ч61
Factorisation theorem 26 82Ч84 89Ч90 112
Formality 29 32Ч34 104Ч105
Formality, 1-formal space 34 36Ч37
Group algebra 124Ч125
Group completion 121Ч128
Group completion, 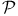 -completion 121 -completion 121
Group completion, k-unipotent see УPro-unipotentФ
Group completion, nilpotent 122 124Ч128
Group completion, pro-finite 7 118 122
Group completion, pro-unipotent 9 29Ч46 123Ч128
Group completion, torsion-free nilpotent 9 43 124Ч128
Group, (pure) braid 8 61
Group, 1-relator 39
Group, abelian 9 116 123Ч125
Group, fibered 27 43 86
Group, finite 6
Group, free 7 9 11 13 16 18 27 38 49 123
Group, free product 8 11Ч14 47 49 109Ч110
Group, Heisenberg 8 39Ч40 49 114
Group, Higman 7 14 85Ч87 110
Group, lattice see УLatticeФ
Group, nilpotent 9 114
Group, non-fibered 27 43Ч45
Group, non-Hopfian 110
| Group, non-linear 85Ч87 110 115Ч119
Group, non-residually finite 7 14 109Ч110 115Ч119
Hard Lefschetz theorem 8 38 130
Harmonic flat bundle 91Ч107
Harmonic flat bundle, deformation theory of 104Ч105
Harmonic map 9Ч10 26 65Ч90
Harmonic map, equivariant 67Ч69 82 92
Harmonic map, existence of 66 68 89
Harmonic map, factorisation of 26 82 89Ч90
Harmonic map, uniqueness of 66
Hermitian sectional curvature 71Ч76
Hermitian symmetric space 78Ч81 85
Higgs bundle 91Ч105
Higgs Ч Hermitian Ч Yang Ч Mills (HHYM) equation 97Ч103
Hodge signature theorem 73
Hodge structure 81 91 129Ч130
Hodge structure, mixed 37 45Ч46
Hodge structure, variation of 94Ч95 107
Holomorphic foliation 24 54Ч63 83Ч84 90
Hyperbolic manifold 8 13Ч14 77Ч78 82Ч85
Hyperkaehler manifold 100Ч103
Isoperimetric inequality 50Ч51
Lattice 7 81Ч83 85 87 95Ч96 110Ч111 115Ч119
Lefschetz hyperplane theorem 5Ч6 11 111Ч113 118
Lie algebra 76Ч81
Lie algebra, deformation of 104
Lie algebra, differential graded (DGLA) 104Ч105
Lie algebra, dual of CDGA 32
Lie algebra, lower central series of 34
Lie algebra, quadratically presented 34 36
Malcev algebra 29 34Ч40 125
Malcev algebra, n-step nilpotent 38 126
Malcev algebra, quadratic presentation of 34Ч38
Massey product 8 38Ч40
Normal variety 9Ч10
Open problem 4 7 9 85 116
Period domain 81 95
Pluriharmonic map 10 71Ч90
Pluriharmonic map, equivariant 72 93
Quasi-isomorphism, of CDGAs 30
Quasi-isomorphism, of DGLAs 104Ч105
Siu rigidity theorem 80
Siu Ч Beauville theorem 2Ч3 8 25Ч28 43
Siu Ч Sampson theorem 71Ч76 89 92Ч93 96 107
Symplectic, form 3 5 18
Symplectic, manifold 5 15Ч20 81
Symplectic, structure 3 5 16 18
Symplectic, sum 17Ч18
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



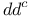 lemma
lemma 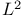 -cohomology
-cohomology 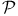 -completion
-completion