Авторизация
Поиск по указателям
Attouch H., Buttazzo G., Michaille G. — Variational Analysis in Sobolev and BV Spaces: Applications to PDEs and Optimization
Обсудите книгу на научном форуме Нашли опечатку?
Название: Variational Analysis in Sobolev and BV Spaces: Applications to PDEs and OptimizationАвторы: Attouch H., Buttazzo G., Michaille G.Аннотация: For graduate students and researchers, Attouch (mathematics, U. Montpellier II, France) et al. present a guide to variational analysis, optimization, and partial differential equations (PDEs). After discussing the basics, the authors chart new areas of research on BV spaces. Topics include weak solution methods, abstract variational principles, complements on measure theory, Sobolev spaces, examples of classical variational problems, the finite element method, spectral analysis of the Laplacian, convex duality and optimization, relaxation, integral functionals, application in mechanics and computer vision, and shape optimization problems.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 2006Количество страниц: 634Добавлена в каталог: 02.02.2010Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
425 390 390 371 383 212 174 25 61 129 133 138 16 129 16 432 121 313 167 152 154 185 563 125 139 124 124 421 124 409 409 394 404 167 153 421 154 101 390 7 464 465 465 124 16 17 181 112 114 138 135 124 125 138 331 389 397 132 309 180 Absolutely continuous 125 Approximate, derivative 408 Approximate, limit 389 Approximate, limit inf 390 Approximate, limit sup 390 Cantor part 407 Cantor set 122 Cantor — Vitali function 408 518 Caratheodory criterion 112 Cauchy — Riemann 9 Coercive 76 Coercive, 589 Coercivity 86 Complementary problem 340 Complementary slackness condition 345 356 Concentration 50 Convolution 18 Courant — Fisher 290 291 294 Covering, fine 115 De La Vallee-Poussin criterion 518 519 Density point 388 diam(E) 109 Dirac mass 15 27 Dirichlet 598 Dirichlet, problem 31 distribution 17 Distribution, derivation 24 div 9 dom f 77 Domain 77 Dual function 354 358 361 Dual problem 351 354 Dual value 354 Duality, gap 354 358 Dunford — Pettis theorem 145 Eberlein — Smulian theorem 56 Eigenvalue 279—281 Eigenvector 280 281 286 288 290 Ekeland's 98 epi f 79 Epi-sum 312 328 Epiconvergence 466 Ergodic theorem 49 Ergodic, dynamical system 534 Ergodic, subadditive ergodic theorem 534 Exact minorant 331 333 Extension, operator 174 Extension, theorem 179 F* 321 Fenchel, extremality relation 332 364 Fenchel, extremality relations 335 Fenchel, Fenchel — Moreau theorem 321 Fenchel, Legendre — Fenchel, conjugate 320 Fenchel, Legendre — Fenchel, transform 597 Finite perimeter (set of) 396 Galerkin approximating method 257 Galerkin method 73 Gateaux differentiability 98 Gauss 8 Gauss — Green formula 396 401 Generalized solution 420 Hahn — Banach separation theorem 92 Hahn — Banach theorem 307 454 Harmonic function 7 Hat function 261 262 Hausdorff, dimension 120 Hausdorff, measure 109 112 Hausdorff, outer measure 109 hilbert 13 Infcompact function 86 Inner measure-theoretic normal 395 Interpolant 265 Ju, Cu 407 Jump, part 407 Jump, point 394 Jump, set 394 404 Karush — Kuhn — Tucker optimality conditions 341 345 Kernel 10 Lagrange, multiplier vector 346 Lagrange, multiplier vector, characterization of 346 Lagrangian 353 Laplace 8 Lax — Milgram Theorem 67 Lebesgue — Nikodym 592 Legendre — Fenchel, conjugate 361 Limit, analysis 597 Lower semicontinuous regularization 85 Marginal function 348 363 Markov inequality 143 Measure theoretical, boundary 389 Measure theoretical, exterior 388 Measure theoretical, interior 388 Measure, Borel 124 Measure, bounded 125 Measure, counting 593 Measure, Radon 115 125 Measure, regular 61 125 Measure, signed 124 Measure, support 124 Measure, total variation 125 Mollifier 18 Mountain Pass Theorem 100 Narrow 374 Narrow convergence, of Young measures 138 Neumann 598 Neumann, boundary condition 34 Neumann, problem 33 Newtonian potential 7 28 nodes 261 262 Normal cone 338 Optimal value 355 oscillations 49 Palais — Smale compactness condition 99 Perturbation function 360 361 363 365 Picard iterative method 71 Poincare inequality 168 Poincare — Wirtinger inequality 180 400 Poisson equation 8 Primal, problem 353 Primal, value 353 Proper 77 Qf 423 Quasi-continuous representatives 340 Quasi-convex envelope 423 458 Rademacher 379 Radon measure 24 Radon — Nikodym theorem 126 Rarefaction point 388 Rayleigh, Courant — Rayleigh formula 298 Rayleigh, quotient 290 Recession, cone 563 Recession, function 440 478 510 524 592 Recession, functional 555 Reduce boundary 397 Reflexive 55 Regular point 393 Regular, triangulation 264 Relaxation 437 Relaxation scheme 457 Relaxed problem 85 420 Rellich — Kondrakov compact embedding theorem 179 Rellich — Kondrakov Theorem 172 Riemann 9 Riesz, representation theorem 20 48 61 67 129 Riesz, theorem 41 86 Rockafellar theorem 329 Saddle point 354 355 Saddle value problems 354 Self-similar set 123 Separation of variable method 279 305 Set convergence 464 Set of class 174 singular 125 Slater qualification assumption 341 343 344 348 350 351 355 363 Slater, generalized Slater 363 Slicing decomposition 135 Sobolev spaces 24 spt 16 124 Stokes problem 35 Subadditive 593 Subadditivity 110 592 Subdifferential 331 Support function 309 Tangent cone 338 Test function 31 Test functions 15 Tightness, for nonnegative Borel measures 133 Tightness, for Young measure 139 Uniformly convex 52 55 Uniformly integrable 58 144 145 148 450 451 460 Value function 363 Vitali's covering theorem 115 von Neumann's Minimax Theorem 360 Weak* topology 60 Weak, convergence 41 Weak, solution 31 Weak, topology 41 44 Weierstrass, example 12 Weierstrass, theorem 87 Young measure 138 Young measures, 450 Young measures, associated with functions 142 Young measures, generated by functions 143
Реклама
 |
|
О проекте
|
|
О проекте



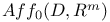
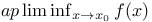
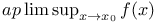
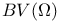
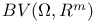
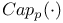
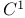 -diffeomorphism
-diffeomorphism 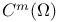
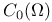
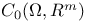
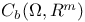
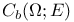
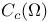
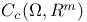
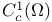
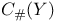
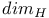
 , f#g
, f#g 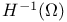
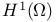
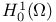
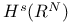
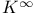

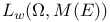
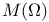

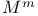
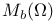
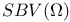
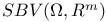
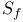
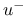 ,
, 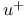
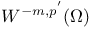
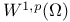
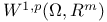

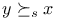
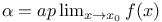

 -convergence
-convergence 
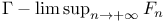
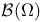
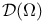
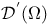

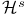
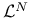
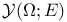
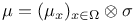
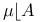
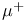 ,
, 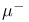
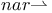
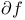
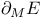
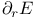
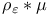
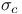
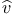
 -coercive
-coercive  -variational principle
-variational principle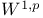 -Young measures
-Young measures