|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Axellson O., Barker V.A. Ч Finite Element Solution of Boundary Value Problems. Theory and Computation |
|
|
 |
| ѕредметный указатель |
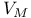 interpolant 170 215 224 230 interpolant 170 215 224 230
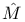 matrix 42 matrix 42
Adjoint operator (see Operator)
Adjoint problem (see Boundary value problem)
Admissible function 65 73 130
Affine variable transformation 172 174 178 190 208 219 235 237 247 250 291
Almost-every where property 103
Anisotropic body 94 199
Array, BONODE 168 180 198
Array, EDGE 168 180 195Ч196
Array, ELNODE 168 180 189 191 196
Array, G 180 185 194
Array, INTPT 180 192
Array, k 180 185Ч187
Array, NODECO 168 180 191 196
Array, PHI 181 192
Array, PHIX 181 192
Array, PHIY 181 192
Array, W 181 192
Aubin Ч Nitsche method 227Ч229 373
Back substitution 280 287
Band matrix 269Ч278 286 385
Band matrix, bandwidth 270
Band matrix, half-bandwidth 270 286
Band matrix, size of band 277 278
Band matrix, variable bandwidth 271 286Ч287 289
Barycentric coordinates 400
Basic two-level grid step 396
Basis functions (see Finite element basis functions)
Basis functions, complete set of 148
Basis functions, dimension-dependent 148Ч149
Basis functions, dimension-independent 148Ч149 151
Biharmonic equation 88
Bilinear form 106 118
Bilinear form, boundedness property 118
Bilinear form, coerciveness property 118
Bilinear form, symmetry property 106 118
Biquadratic polynomial 249
Block Ч SSOR preconditioning 337 408Ч412
Boundary condition, Dirichlet 83 95 143 233Ч234 327 338 373
Boundary condition, essential 74Ч80 82Ч83 87Ч88 90-91 112 120 168 185 204
Boundary condition, inhomogeneous 127Ч130
Boundary condition, mixed 84 129
Boundary condition, natural 74Ч80 82Ч84 87Ч88 90Ч92 95 112 120Ч121 168 185 203Ч204
Boundary condition, Neumann 83 95 334 336 338 358
Boundary condition, periodic 98
Boundary condition, third type (Robin) 84
Boundary value problem (see Boundary condition)
Boundary value problem in context of Lax-Milgram lemma 120Ч122
Boundary value problem, adjoint problem 121Ч122 228
Boundary value problem, classical solution of 102 121
Boundary value problem, definition of 64
Boundary value problem, fourth-order 71Ч73 85Ч89 95 171
Boundary value problem, generalized solution of 102 121 129Ч130 137 159
Boundary value problem, self-adjoint property 121
Boundary value problem, sources of 92Ч95
Boundary value problem, two-point 69Ч73 78 230
Boundary value problem, variational formulation of 69 72 107 113 115 135 182 228 245Ч246
Brachistochrone problem 96 98
Bramble Ч Hilbert lemma 219 221Ч223
Cauchy sequence 104 108Ч109 114 132
Cauchy Ч Schwarz inequality 5 104 108 120 123 131 138 216 342 397
Chebyshev iteration 395
Chebyshev polynomial 26 422Ч425
Cholesky factorization 284 290 295 298Ч299 315 317
Cholesky method (see Cholesky factorization)
Compact support 115 117
Complete polynomial 170
Completion of a set of admissible functions 101 107Ч113
Computational labor, conjugate gradient method (simple) 23Ч24 52 384 388Ч391
Computational labor, direct methods 286Ч287 302Ч303 385 388Ч391
Computational labor, multigrid methods 397 406
Computational labor, preconditioning by incomplete factorization 52 56 369Ч373 384 388
Computational labor, SSOR preconditioning 52 56 384 388Ч391
Computer programs that implement direct methods 307
Condensed matrix (see Superelement matrix)
Cone condition 222
Congruence transformation 284 288
Conjugate gradient method (simple) 18Ч28
Conjugate orthogonality 22
Conormal derivative 126
Consistency condition 125
Continuity condition of current flow 93
Convergence in the mean 104
Convex functional 58
Convex subset 57
Critical term 242Ч243
Cuthill Ч McKee algorithm 276
DATA ERROR 308 369 374 376Ч378 381
Data structure (see Storage scheme)
Data transfer 286Ч287 289 306
Defect-correction method 393Ч394
Deflection of a frame 205Ч206
Deflection of a plate 87Ч89
Deflection of abeam 77Ч78 135Ч136
Degree of freedom 171
Degree of graph node 276
Density of nonzero entries in matrix band 277Ч278
Descent direction 10
Diagonal scaling 56 59 238 317 376
Diagonally dominant matrix 42 203 337
Diffusion 94
Dirac delta function (see Symbolic function)
Direct method 279 (see also Cholesky factorization)
Directional derivative 5 66
Discontinuous coefficient 238 245Ч247 332 336 338 383 392
Discretization error 214Ч215 226Ч232 241 244 246 313 386 388 391 406
Discretization error, 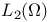 norm of 227Ч229 norm of 227Ч229
Discretization error, maximum norm of 230Ч232
Discretization error, pointwise 231Ч232
Discretization error, Sobolev norm of 226Ч227
Double-precision accuracy 287 315 377 382
Dual space 131
Edge integral 194Ч198
Edge ratio 225Ч226 238 315
Effective spectral condition number 27
Eigenfunction 149 390 394
Eigenvalue cluster 28
Elemeni mass matrix 234
Elemeni mass matrix for model problems 259 260
Elemeni stiffness matrix (see Element matrix)
Element (of a finite element mesh) 165
Element (of a finite element mesh), degenerate 169
Element (of a finite element mesh), rectangular 177Ч179 225Ч226 249-250 362
Element (of a finite element mesh), Serendipity 250 402
Element (of a finite element mesh), standard 172 174 177 178 189 192Ч193 196 207 219 222 225 235 237
Element (of a finite element mesh), triangular 167 173Ч177 219 224 232 248Ч249 362 364
Element matrix 188Ч191 199Ч202 206 308 363 379
Element matrix for model problems 252Ч254 292 314Ч315 415Ч416
Element matrix, modified 294Ч295
Element vector 193Ч194 308 379
Element vector, modified 294Ч295
Elementary operation 279
Elliptic regularity 229 373 390
Energy inner product of two functions 108 121
Energy inner product of two vectors 13
Energy norm of a function 108 121
Energy norm of a vector 13
Envelope of a matrix 39 270Ч276 278 286 289 300
Equilibrium equation of heat flow 95
Equivalence class 102Ч103 112 170
Equivalent norms 114 119 121
Euclidean norm 3
Euler-Lagrange equation one space dimension 65Ч73 107
Euler-Lagrange equation, several dependent variables 90Ч92
Euler-Lagrange equation, three space dimensions 89Ч90
Euler-Lagrange equation, two space dimensions 80Ч89
Extension operator 395
Field equation 92Ч95
fill factor 304
| Fill-in 39 41 268 272 278 289 373
Fill-in matrix 370 373
Finite element basis functions, accuracy parameter k 170 173 176Ч177 179 209 217 224 226
Finite element basis functions, conforming 171
Finite element basis functions, global 168Ч171 175 179
Finite element basis functions, isoparametric 190 207Ч213
Finite element basis functions, local 171Ч173 175
Finite element basis functions, piecewise bilinear 177Ч179 200Ч203 272 277 301 327 337Ч338 340 360 401
Finite element basis functions, piecewise linear 173Ч176 200Ч203 215 232 277 305 314Ч315 327 330 337Ч340 344 360 364 371 379Ч380 388 393 404
Finite element basis functions, piecewise quadratic 176Ч177 277 290 301 364 393
Finite element basis functions, Serendipity 250 402
Finite element basis functions, singular isoparametric 244
Finite element basis functions, standard local 172Ч174 177Ч178 190 207 222 290
Finite element basis functions, support of 169
Finite element mesh 165Ч168 207 Node)
Finite element mesh, automatic generation 167Ч168
Finite element mesh, family 226 235
Finite element mesh, nonuniform 163 244 313 315
Finite element mesh, refinement of 167 202 204 244 367Ч368 374
Finite element mesh, regular family 226
Finite element space 168
Finite termination property 24
FLOP 52 286Ч287
Formal adjoint (see Operator)
Forward substitution 287
Fourier expansion 152 241
Friedrichs' second inequality 124
FriedrichsТ first inequality 123
Frontal method 305Ч307
Functional 2Ч3 65 67 71 81 85Ч90 94 105 119 Quadratic
Galerkin method, application to noncoercive problems 155Ч160
Galerkin method, error analysis 154
Galerkin method, formulation of 153Ч154
GardingТs inequality 159
Gauss Ч Seidel relaxation 395
Gaussian elimination 279Ч287
Gaussian elimination, pivoting in 281Ч282 311
Gaussian elimination, row-wise 282Ч287
Gaussian elimination, stability of 281 310Ч312
Gaussian elimination, symmetric 283Ч287
Gaussian factorization (see Gaussian elimination)
Generalized derivative 109Ч110 114 116Ч117 120
Generalized eigenvalue problem 365
Gradient error 227 391
Gradient function 99
Gradient vector 3 (see also Residual vector)
Gradient vector, recursive computation of 12 22 375
Green's function 136Ч139 230Ч232
Growth factor 42 44 311
Heaviside unit step function 133
Hessian matrix 4
Hilbert space (see Sobolev space)
Hilbert space, 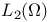 115Ч116 115Ч116
Hilbert space, ![$L_{2}[a, b]$](/math_tex/c9e8f89bb0f262f794e6326c7b78332d82.gif) 102Ч105 102Ч105
Hilbert space, arbitrary 118
Hilbert space, completeness property 104 109 119 160
Homogeneous body 94
Householder matrix 287Ч289
III-conditioned system 232 282
Inhomogeneous body 94
Integration by parts 81
Interface condition 246
Interface corner 247
Internal boundary (see Material interface)
Interpolation in multigrid methods 395
Interpolation, error analysis of 215Ч226 246
Interpolation, Hermite 171 224Ч225
Interpolation, Lagrange 171 224
Inverse estimate 239
Inverse iteration 317
Isotropic body 94
Iterative refinement 38 315Ч316 369 391Ч392
Jacobian 189 219 225 235 237
L matrix 339
Law of Sines 259
Lax Ч Milgram lemma 118Ч130 135Ч136 145Ч146 150 152Ч155 160 245
Least squares 161
Lebesgue integral 102 115
Level structure (see Matrix graph)
Level surface 6
Line search 11
Linear functional 105 119 130 137 145 221
Linear functional, boundedness property 105 119
Linear functional, derivative of 133
Linear space 65 103
Local support 163 169
Machine precision parameter 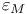 310Ч311 314 374 384 310Ч311 314 374 384
Mass matrix 233Ч236
Mass matrix, spectral condition number of 236
Material interface 245Ч247
Matrix graph 272Ч276
Matrix graph, edge of 272
Matrix graph, level structure of 274Ч276
Matrix graph, node of 272
Matrix graph, rooted level structure of 274
Matrix graph, separator of 300
Matrix graph, set of paths of 339Ч340
Matrix graph, tree 322
Matrix partitioning method 297Ч300
Maximizer of a functional 3
Maximum angle condition 226
Maximum principle 257
Measure of a point set 103 122
Measure zero property 103 116
Method of steepest descent 9Ч15
Minimizer of a functional global 3 65
Minimizer of a functional local 3 65
Minimizer of a functional strong global 3 65
Minimizer of a functional strong local 3 65
Minimum angle condition 226
Minimum condition number 316
Mixed variational formulation 95 171
Multi-index notation for a partial derivative 116
Multigrid method 392Ч407
NavierТs equations 92
Neighborhood 3 65Ч66
Nested dissection 301Ч305
Nested dissection, ordering 304Ч305 387Ч388
Node (of a finite element mesh) 165
Node (of a finite element mesh), coordinates of 191
Node (of a finite element mesh), edge 165
Node (of a finite element mesh), global ordering of 167 186 268Ч269 281
Node (of a finite element mesh), interior 165
Node (of a finite element mesh), local ordering of 167 175 177Ч178 195
Node (of a finite element mesh), vertex 165
Numerical integration 191Ч193 213 232 254Ч255
Numerical integration, Gauss Ч Legendre formula 197 254
Numerical integration, integration point 191
Numerical integration, integration weight 191
Numerical stability (see Stability)
Oblique derivative 143
OhmТs Law 94
One-way dissection ordering 300Ч301
Operator 107
Operator, adjoint of 122
Operator, formal adjoint of 122
Operator, linear property 107
Operator, self-adjoint (symmetric) property 121Ч122
Optimal error estimate 151
Optimal order process 404
Penalty method 143 161Ч162
Perturbation function (see Test function)
Perturbation of a linear system 308Ч310
Petrov Ч Galerkin method 154 262
Piecewise differentiable function 112
Piecewise polynomial 117 169
Pointwise convergence 104
Polar coordinates 241
Polar-coordinate element 244
Preconditioned conjugate gradient method (see Computational labor Preconditioning Preconditioning SSOR
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



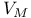 interpolant
interpolant 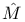 matrix
matrix 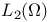 norm of
norm of ![$L_{2}[a, b]$](/math_tex/c9e8f89bb0f262f794e6326c7b78332d82.gif)