|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Abels H. — Finite Presentability of S-Arithmetic Groups: Compact Presentability of Solvable Groups (Lecture Notes in Mathematics) |
|
|
 |
| Предметный указатель |
Abelianization of a group 2.3.5
Abelianization of a Lie algebra 2.1
Arithmetic group 0.2.1 6.1.1 7.1.2
Associated graded Lie algebra of a filtered group 2.3.3
Associated graded Lie algebra of a filtered Lie algebra 2.1
Bieri — Strebel invariant 3.4 7.3.1
Borel subgroup 6.4.1
Campbell — Hausdorff formula 2.5
CHARACTER 0.2.15 6.2.2
Colimit 4.2
Commensurable (subgroups) 5.3.1 7.1.2
Commutator 2.2.2 2.1
Compact presentation 1.1
Contracting (automorphism) 0.3.3 1.2
Derived group 2.3.5
Descending central series of a group 2.3.4
Descending central series of a Lie algebra 2.1
Divisible group 2.4.1
Expanding (automorphism) 1.2
Field, local 1.2 2.6
Field, p-adic 2.6
Filtered group 2.3.2
Filtered Lie algebra 2.1
Filtered topology given by a filtration 2.1.4
Function field 0.4.7
Generators 1.1
Graded Lie algebra 1.2.7
Group, arithmetic 0.2.1 6.1.1 7.1.2
Group, compactly generated 0.2.8 1.1 3.2.2 6.2.5
Group, compactly presented 0.2.8 1.1 5.6.1 6.2.3
Group, divisible 2.4.1
Group, finitely presentable, finitely presented 0.1 0.2 0.3 6.1 6.2.4 7.0
Homology of a group 5.1.3
Homology of a Lie algebra 5.2.1
Hopf extension for groups 5.1.2
Hopf extension for Lie algebras 5.2.2
Koszul complex 5.2.1
Lattice 5.3
Lie algebra, filtered 2.1
Lie algebra, graded 1.2.7 2.1 2.3.3
Lie algebra, nilpotent 2.1
Lie ring [= Lie algebra over  ] 2.6 2.5.12 ] 2.6 2.5.12
Linear algebraic 0.2.1
| Linear algebraic, split 6.4
Linear algebraic, split solvable 6.2.1
Linear algebraic, trigonalisable 6.2.1
Linear algebraic, type 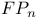 0.4.1 7.4.10 0.4.1 7.4.10
Local field 1.2 2.6
Malcev correspondence 5.3.5
Module (of a local field) 1.2
Nilpotent 2.3.7
Nilpotent group 2.3.7
Nilpotent Lie algebra 2 . 1
Nilpotent Lie group over k 2.5
p-divisible 2.4.1
p-Divisible group 2.4.1
P-isolator 2.4.3
P-number 2.4.1
P-radicable 2.4.1
P-radicable group 2.4.1
Positive dependence, positively dependent 3.2.1 Appendix
Presentation 1.1
Radicable 2.4.1
Radicable group 2.4.1
Reflection (of  with respect to a root with respect to a root  ) 6.6.1 ) 6.6.1
Relations 1.1
Root 6.3.1
Root system 6.4.1
Root, inverse 6.6.1
Root, simple 6.4.1
S-arithmetic 0.2.3 6.1.1 7.1.2
S-arithmetic group 0.2.3 6.1.1 7.1.2
Split solvable linear algebraic group 0.2.10 6.2.1
Tame 7.3.10
Tame group 7.3.10
Tame representation 0.2.15
Torus, split 0.2.10
Type 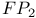 0.4.1 7.0 7.3.10 7.4.10 0.4.1 7.0 7.3.10 7.4.10
Type 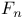 0.4 0.4
Type 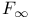 0.4 0.4
Unipotent endomorphism 0.2.6
Unipotent radical 0.2.6
Weight 0.2.15 3.1 7.3.2
Weight space 0.2.15 3.1 7.3.2
Weight, dominant 6.4.1
Weyl chamber 6.4.1
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 ]
] 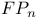
 with respect to a root
with respect to a root  )
)