Авторизация
Поиск по указателям
Aarts J.M., Nishiura T. — Dimension and Extensions (North-Holland Mathematical Library)
Обсудите книгу на научном форуме Нашли опечатку?
Название: Dimension and Extensions (North-Holland Mathematical Library)Авторы: Aarts J.M., Nishiura T. Аннотация: Two types of seemingly unrelated extension problems are discussed in this book. Their common focus is a long-standing problem of Johannes de Groot, the main conjecture of which was recently resolved. As is true of many important conjectures, a wide range of mathematical investigations had developed, which have been grouped into the two extension problems. The first concerns the extending of spaces, the second concerns extending the theory of dimension by replacing the empty space with other spaces. The problems of De Groot concerned compactifications of spaces by means of an adjunction of a set of minimal dimension. This minimal dimension was called the compactness deficiency of a space. Early success in 1942 led De Groot to invent a generalization of the dimension function, called the compactness degree of a space, with the hope that this function would internally characterize the compactness deficiency which is a topological invariant of a space that is externally defined by means of compact extensions of a space. From this, the two extension problems were spawned. With the classical dimension theory as a model, the inductive, covering and basic aspects of the dimension functions are investigated in this volume, resulting in extensions of the sum, subspace and decomposition theorems and theorems about mappings into spheres. Presented are examples, counterexamples, open problems and solutions of the original and modified compactification problems.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Издание: 1st editionГод издания: 1993Количество страниц: 331Добавлена в каталог: 10.12.2009Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
282 6 29 (see “Roy’s example”) 303 302 6 301 301 160 288 49 49 58 94 109 85 100 85 100 142 158 Absolute 31 Absolute additive Borel class 115 Absolute Borel classes 115 Absolute multiplicative Borel class 115 Absolutely closed-monotone 78 Absolutely monotone 82 Absolutely open-monotone 110 Addition theorem 6 Additive Borel class 114 Additive in U 130 Ambiguous 231 Axioms A 178 Axioms Al 180 Axioms H 175 Axioms H extended 176 Axioms M 171 Axioms N 172 Axioms S 179 Axioms Sh 180 Base for the closed sets 251 Base-normal (base) 259 Base-normal (space) 259 Basic inductive dimension modulo 218 Border structure of order n 308 Borel set 112 Boundary dimension 305 Brouwer fixed point theorem 12 class 74 Closed-additive in 130 Closed-monotone 77 Closed-monotone in 77 Coincidence theorem 10 Combinatorially equivalent 88 96 Compactification problem 16 Compactness deficiency 16 Complementary 231 complete 28 Completeness deficiency 34 Completeness order dimension 40 Cosmic family in 142 Countable sum theorem 6 Countably closed-additive in 142 Cover 42 Covering completeness degree 49 Covering dimension 42 de Groot’s problem 16 de Groot’s theorem 15 280 Decomposition theorem 6 Deep inside 300 Deficiency, compactness 16 Deficiency, completeness 34 Deficiency, large 109 Deficiency, small 109 Degree, covering completeness 49 Degree, large compactness 21 Degree, large inductive 54 Degree, large inductive compactness 20 Degree, large inductive completeness 33 Degree, small inductive 54 Degree, small inductive compactness 15 Degree, small inductive completeness 33 Diameter 30 Dimension of a mapping 206 Dimension offset 208 Dimension, basic inductive modulo 218 Dimension, boundary 305 Dimension, completeness order 40 Dimension, covering 42 Dimension, large covering modulo 94 Dimension, large inductive 9 Dimension, large inductive modulo 80 Dimension, mixed inductive 241 Dimension, order 25 Dimension, order modulo 234 Dimension, proximity 303 Dimension, small covering modulo 94 Dimension, small inductive 3 Dimension, small inductive modulo 76 Dimensionsgrad 2 Disjunction property 251 Disjunctive 259 Distributive 248 Dowker space 182 Dowker universe 156 Dowker-open 149 Dual ideal 249 Enclosure 49 94 Equimorphism 301 Example, Kimura’s 68 Example, Pol’s 62 Example, Roy’s 9 Excision theorem 224 expansion 226 Extendable 304 Extension 28 FAR 300 Framework of a base 219 Freudenthal base 267 Freudenthal compactification 267 Hayashi sponge 165 Hereditary with respect to 32 Homomorphism 249 Ideal compactification 266 Inductive invariants 126 Isomorphic 249 Isomorphism 249 Join 248 Kimura’s example 68 Kimura’s theorem 68 297 Large 109 Large compactness degree 21 Large covering dimension modulo V 94 Large inductive compactness degree 20 Large inductive completeness degree 33 Large inductive dimension 9 Large inductive dimension modulo 80 Lattice 248 Lavrentieff’s theorem 31 Lindeloef at infinity 272 Locally finite sum theorem 39 Locally finitely closed-additive in W 142 Maximal 249 Meet 248 Mixed inductive dimension 241 Modulo notation 50 87 Monotone 82 Monotone in 82 Multiplicative Borel class 114 NEAR 300 Normal base 259 Normal family extension 147 Normal family in 142 Normal universe modulo 99 Open cover 42 Open-monotone 110 Open-monotone in 110 Operation 140 Operation 140 Operation 147 Operation 151 Order dimension 25 Order dimension modulo 234 Order of a cover 41 Order of a mapping 206 Order offset 209 Oscillation 30 Partition 3 Perfect compactification 270 Point addition theorem 8 Point-additive in 130 Polish space 117 Pol’s example 62 Product theorem 7 Proximal 300 Proximity dimension 303 Proximity relation 300 Proximity space 300 Quasi-component 275 Quasi-component space 275 Rational curve 15 refinement 42 Regular curve 15 Regular family in W 142 Regularly closed 267 Regularly open 267 Relative dimension 199 Remainder 302 Rim-compact 14 Ring 259 Roy’s example 9 S-deficiency 58 S-hull 58 S-kernel 55 screening 259 Screening collection 266 Semi-normal family in U 142 Separated 84 Shrinking 42 Small 109 Small covering dimension modulo 94 Small inductive 54 Small inductive compactness degree 15 Small inductive completeness degree 33 Small inductive dimension 3 Small inductive dimension modulo 76 Stable value modulo 89 Strongly closed-additive in 130 Strongly hereditarily normal 150 Strongly paracompact 160 Structure theorem 40 Subspace Theorem 5 Super normal 182 Swelling 88 S—Surplus 55 Theorem Addition 6 Theorem, Brouwer fixed point 12 Theorem, coincidence 10 Theorem, countable sum 6 Theorem, de Groot’s 15 280 Theorem, decomposition 6 Theorem, excision 224 Theorem, Kimura’s 68 297 Theorem, Lavrentieff’s 31 Theorem, locally finite sum 39 Theorem, point addition 8 Theorem, product 7 Theorem, structure 40 Theorem, subspace 5 Theorem, Tumarkin’s extension 32 Topologically invariant class 74 Totally normal 147 Tumarkin’s extension theorem 32 Universe of discourse 74 Unstable value modulo 89 Wallman compactification 254 Wallman compactification with respect to a base 260 Wallman representation 251 Weight 262 Zero-dimension ally embedded 268 Zero-set 255
Реклама
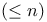-Inductionally embedded 
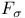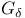-set 
-set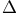 
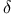-cover 
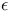-mapping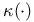 
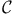-border cover 
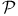-border cover 
-locally finitely closed-additive in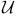 
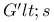-space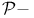 
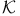-border cover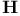 
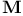
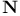
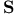
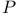-deficiency 
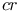-compactness degree 
|
|
О проекте