|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Maric V. — Regular Variation and Differential Equations |
|
|
 |
| Предметный указатель |
Abelian theorems V
Ackerberg, R.C. 105 119
Aljancic, S. 119
Asymptotic inverse 99
Avakumovic, V.G., V 5 72 74 89 119
Balkema, A.A. 72
Bari, N.K. 5 119
Bekessy, A. 4 119
Bellman, R. 67 119
Bingham, N.H., V 119
Bojanic, R. 119
Cauchy principle 20
Cauchy — Schwartz inequality 60
Coppel, W.A. 56 119
De Haan, L., V 1 72 115 120
De Haan’s class 2 6
Differential equations of boundary layer theory 1 105
Differential equations of ferroelectrical phenomena 90
Differential equations, Airy 45
Differential equations, Emden — Fowler 72 89 101
Differential equations, Euler 14
Differential equations, Legendre 44
Differential equations, Poisson 71
Differential equations, Prandtl 105
Differential equations, Riccati 33
Differential equations, Schrodinger 1
Differential equations, second order linear 1 7 8 9
Differential equations, second order linear general 41
Differential equations, second order linear selfadjoint 43 45
Differential equations, second order nonlinear 1
Differential equations, Thomas-Fermi (atomic model) 71 89
Eastham, M.S.P. 119
Fedoryuk, M.V. 120
Feller, W., V 120
Fermi, E. 120
Fowler, R.H. 72 89
Functions of class 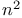 46 46
Functions of class II 6 22 46 47 70
Functions of class r 6 22 64 65 118
Functions, almost decreasing 5 56 76 77 82 97 98 117
Functions, almost increasing 5 77 81 97 117
Functions, Beurling slowly varying 7 22 24 62 63 64 118
Functions, convex 75
Functions, logarithmico-exponential 7
Functions, rapidly varying 2 4 72 90 91 117
Functions, rapidly varying at zero 90 92
Functions, regularly bounded 2 5 76 81 117
Functions, regularly bounded at zero 76 82
Functions, regularly varying at zero 5 86 89 92 99 105
Functions, regularly varying, V 2 3 12 14 23 33 64 72 86 87 89 91 93 99 116 117
Functions, slowly varying 2 3 7 23 61 66 67 81 82 91 92 93 115 117
Functions, slowly varying at zero 82 93 115
Functions, slowly varying normalized 3 12 15 30 31 32 37 40 41 42 43 51
Functions, smoothly varying 72
Functions, superlinear 102
Geluk, J.L., V 22 46 70 72 74 120
Germs of real-valued functions 7
Goldie, C.M., V 119
Green, G. 1 120
Grimm, L.J. 43 120
Hacik, M. 62 70 120
Hall, L.H. 43 120
Hardy field 7
Hardy, G.H., V 7 121
Hartman, Ph. 55 56 70 121
Heading, J. 121
Hille’s criterion 27
Howard, H.C., V 121
Its, A.R. 69 121
Karamata class 1 2 5 12 21 26 27 91
| Karamata, J., V 1 2 5 115 121
Kohlbecker, E.E. 3 121
Lebesgue dominated convergence theorem 30
Liouville Green approximation 45 67 69
Liouville, J. 1 122
Littlewood, J.L. V
Marie, V. 12 75 91 120 121 122 123
Marik, J. 62 123
Marini, M. 10 123
Me Leod, J.B. 105 106 107 109 123
Mercerian theorems V
Murray, J.D. 123
Nayfeh, A.H. 123
Nonstandard asymptotic analysis 114
Olwer, F.W.J. 123
Omey, E., V 12 22 46 62 70 120 123 124
Phase integral method 69
Potter’s criterion 46
Rab, M. 62 123
Radasin, Z. 91 106 121 122 123
Representation theorem 3 9 13 15 31 33 36 40 42 52
Representation theorem for regularly, bounded functions 40
Rosenlicht, M. 124
Sataric, M.V. 90 124
Seneta, E., V 124
Shemsidini, Z.Y. 124
Slavyanov, S.Yu. 124
Solutions of a boundary layer equation, existence of 105 107
Solutions of a boundary layer equation, regular boundedness of 105 113
Solutions of a boundary layer equation, regular variation and asymptotic behaviour of 105 113
Solutions of a boundary layer equation, uniqueness of 105 109
Solutions of equations of Thomas-Fermi type, regular boundedness of 76
Solutions of equations of Thomas-Fermi type, regular variation and asymptotic behaviour of 72 83
Solutions of equations of Thomas-Fermi type, slow variation and asymptotic behaviour of 83
Solutions of second order linear equations of class  24 24
Solutions of second order linear equations of class 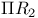 21 46 47 21 46 47
Solutions of second order linear equations of class  22 23 22 23
Solutions of second order linear equations, nonoscillatory 8 26 27 28 30 43 46 68
Solutions of second order linear equations, nonprincipal 19
Solutions of second order linear equations, oscillatory 8 26 27 69
Solutions of second order linear equations, principal 19
Solutions of second order linear equations, rapidly varying; asymptotic behaviour of 69
Solutions of second order linear equations, rapidly varying; existence of 17 19 21 44 45
Solutions of second order linear equations, regularly bounded 26 40 68
Solutions of second order linear equations, regularly varying, existence of 12 14 19 21 26 27 32 41 42 43
Solutions of second order linear equations, regularly varying; asymptotic behaviour of 58 61 62
Solutions of second order linear equations, slowly varying; asymptotic behaviour of 49 51 52 54
Solutions of second order linear equations, slowly varying; existence of 12 19 21 30
Solutions of second order linear equations, zeros of 62 63 64
Steckin, S.B. 5 119
Stirling’s formula 100
Sturm separation theorem 26
Successive approximations method 28 34 38 50
Swanson, C.A. 124
Taliaferro, S. 74 91 102 104 124
Tauberian theorems, V 72
Teugels, J.L., V 119
Thomas, L.H. 124
Tomic, M., V 12 26 75 119 120 122
Tuszynski, J.A. 124
Uniform convergence theorem 3
Van der Berg, J.P. 114 119
Wiener, N. V
Willekens, E. 46 124
Willett, D. 124
Wintner, A. 55 56 70
WKBJ method 69
Wong, P.K. 74 82 124
Wronski, H. 9 10
Zakula, R.B. 124
Zezza, P. 10 123
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте